之前我在网上搜索有关卡尔曼滤波器中P,Q,R矩阵的设置,感觉讲述得比较笼统。又因为我要使用雷达目标跟踪方面使用卡尔曼滤波器,因此针对雷达中目标匀速运动的情况来说明一下P,Q,R矩阵的设置。
1.卡尔曼滤波器变量转移情况分析
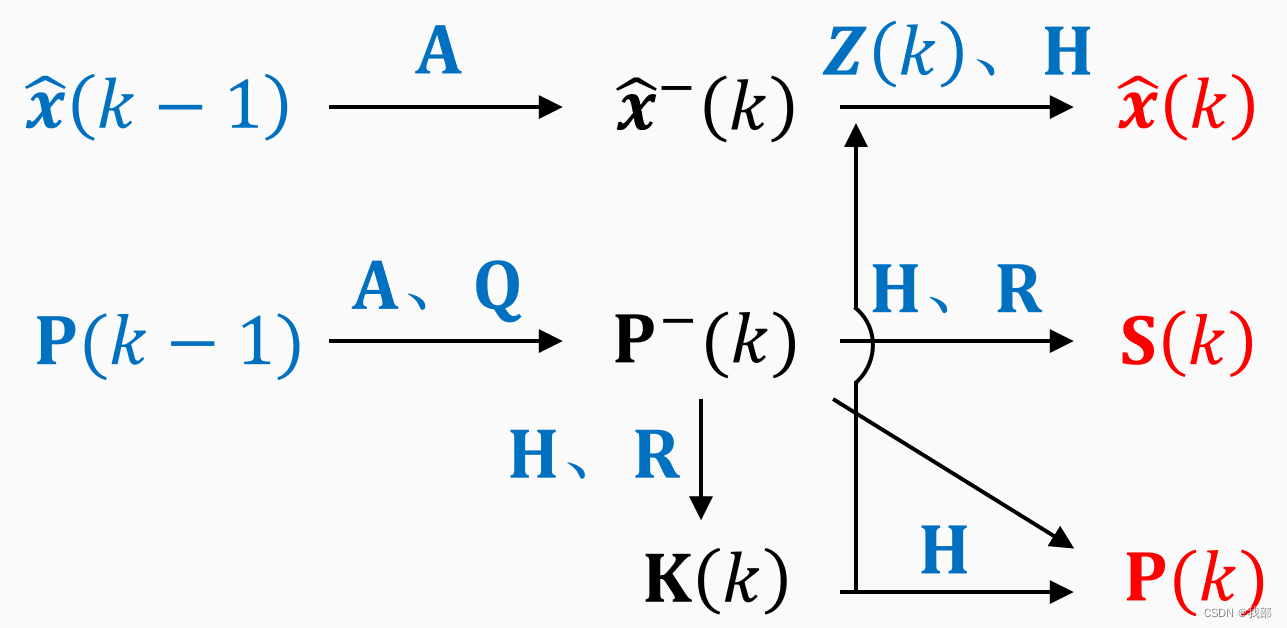
首先,我们可以画出卡尔曼滤波器中的变量计算的先后顺序,如下图所示。变量的含义在图后有说明。因为是匀速运动,因此A(运动方程)和H(量测矩阵)都是已知的,特别注意的一点是我的整个过程都是在笛卡尔坐标系进行的。另外Z(K)是当前K时刻的量测点,也是已知的。因此只需要确定![]()
讯享网,P(K),Q和R的初值。
2.P矩阵的设置
对于![]() 的初值,可以根据航迹中已知的前两个点来确定。对于P矩阵初值的设定,可以参考论文[1]。其中的公式为:
的初值,可以根据航迹中已知的前两个点来确定。对于P矩阵初值的设定,可以参考论文[1]。其中的公式为:
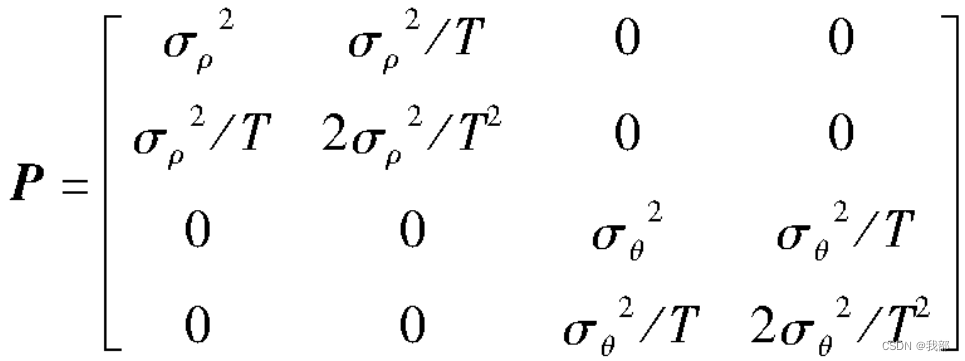
![]() 是径向距离的观测噪声方差,
是径向距离的观测噪声方差,![]() 是方位角的观测噪声方差,这是P矩阵在极坐标系下的表示(因为雷达检测的数据是这样的)。之前有说到,我们目标跟踪是在笛卡尔坐标系下进行的,因此P矩阵还要进行坐标系转化,也就是要知道径向距离和方位角的观测噪声方差与直角坐标系x轴和y轴的观测噪声方差的关系。这在之后会有说明。
是方位角的观测噪声方差,这是P矩阵在极坐标系下的表示(因为雷达检测的数据是这样的)。之前有说到,我们目标跟踪是在笛卡尔坐标系下进行的,因此P矩阵还要进行坐标系转化,也就是要知道径向距离和方位角的观测噪声方差与直角坐标系x轴和y轴的观测噪声方差的关系。这在之后会有说明。
| 符号 |
含义 |
|
|
转移状态矩阵,描述相邻两帧状态转移关系 |
|
|
量测矩阵,描述目标状态到量测空间的映射关系 |
|
|
控制向量 |
|
|
控制矩阵 |
|
|
过程噪声协方差矩阵 |
|
|
量测噪声协方差矩阵 |
|
|
新息协方差矩阵 |
|
|
卡尔曼增益
|
|
|
第 |
|
|
第 |
|
|
第 |
|
|
估计的协方差矩阵 |
|
|
|
3.R矩阵的设置
接下来说明R矩阵的设置,在匀速直线运动中,如果是极坐标系下的话,R矩阵的形式是:
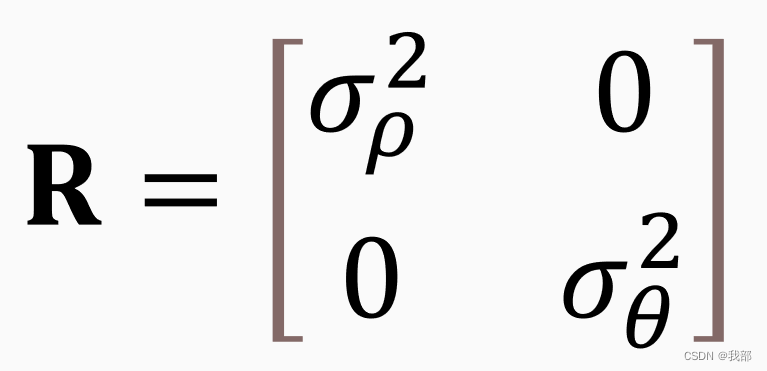
如果转换到笛卡尔坐标系的话,R矩阵的形式要发生改变,并且要对观测噪声的方差进行转换。我是参考的这一本书[2],其中的(11.15)和(11.16)的公式。

其中![]() 是x方向的观测噪声方差,
是x方向的观测噪声方差,![]() 是y方向的观测噪声方差。
是y方向的观测噪声方差。
那么P矩阵其实也可以计算出来,至于P矩阵进行坐标系转换后的数学形式会不会变我没有细想(但感觉是会的)。
4.Q矩阵的设置
接下来是对于Q矩阵的估计,其实我没有特别好的方法,因此我是在P和R矩阵都确定之后,根据以下的公式将Q假设为一个时不变的矩阵:
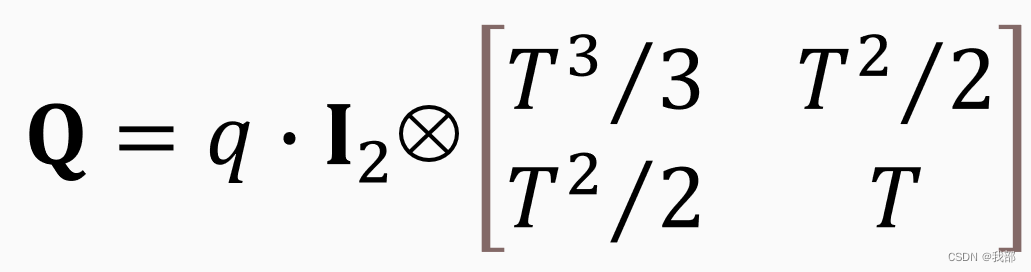
其中,q是过程噪声强度, 是二阶单位矩阵,
是二阶单位矩阵,![]() 是Kronecker积,T表示数据每帧的扫描间隔。(注意,这只是匀速直线运动的情况)
是Kronecker积,T表示数据每帧的扫描间隔。(注意,这只是匀速直线运动的情况)
然后对于q从小到大进行调整,直到目标跟踪的结果比较好就确定了Q矩阵。
[1] 李珂, 王瑞, 宋建强. 基于卡尔曼滤波的雷达单目标跟踪算法研究[J]. 空间电子技术, 2019(1):5.
[2] 吴顺君, 梅晓春. 雷达信号处理和数据处理技术[M]. 电子工业出版社, 2008.


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/22647.html