【SLAM】评估轨迹误差，手写ATE、RPE对比EVO

大家好，我是讯享网，很高兴认识大家。

1.绝对轨迹误差（Absolute Trajectory Error, ATE）

1.1旋转+平移的均方根误差

1.2 仅计算平移的均方根误差

2.相对轨迹误差（Relative Pose Error, RPE）

2.1旋转+平移的均方根误差

2.2平移的均方根误差

3.代码部分

4.evo工具

4.1 evo工具安装以及使用说明

4.2 evo中计算ATE（APE）

4.2 evo中计算RPE

常用评估轨迹误差的方式有两种：绝对轨迹误差（ATE）与相对轨迹误差（RPE）

1.绝对轨迹误差（Absolute Trajectory Error, ATE）

绝对轨迹误差即为求每个位姿李代数的均方根

如图，有两条轨迹，一条为真实轨迹esti，一条为slam算法估算的轨迹gt, 将两条轨迹分为无数个点，并在上面分别取两个点Pesti,i和Pg,i，其相对于原点P的计算公式如下，其中T为欧式变化（属于李群）

讯享网

$P_{esti,i} = T_{esti,i}*P$

$P_{g,i} = T_{g,i}*P$

计算第i个点的误差error的李群形式，写成相除的形式比较好理解：

$error = P_{esti,i} / P_{g,i} = T_{esti,i} * T_{g,i}^{-1}$

1.1旋转+平移的均方根误差

由于我们最终求的是李代数的均方根，所以先求error对应的李代数，提出一个负号（可在代码中验证）

$E_{g,i} =log_e(T_{g,i+\Delta } * T_{g.i}^{-1})^V = - log_e(T_{g.i}^{-1} *T_{g,i+\Delta })^V$

取范数后，取均方根得到ATEall，取范数后正负号不影响

$ATE_{all} =\sqrt{\frac{1}{N}\sum_{i=1}^N||log_e(T_{g,i} ^{-1} *T_{esti,i})^V||_{2}^{2}}$

1.2 仅计算平移的均方根误差

在获取平移的均方根时，不需要转换到李代数，在欧式变换（李群）中取出其平移量计算均方根。

$ATE_{all} =\sqrt{\frac{1}{N}\sum_{i=1}^N||trans(T_{g,i} ^{-1} *T_{esti,i})||_{2}^{2}}$

2.相对轨迹误差（Relative Pose Error, RPE）

2.1旋转+平移的均方根误差

相对轨迹误差是计算相隔 $\Delta t$ 时间的两帧之间位姿之差的精度。（有点绕）

( $\Delta t$ 时间对应可能不止1帧，但是是帧数的整数比如1，2，3...帧)

还是一样，两条轨迹分别为真实轨迹gi，算法估计轨迹esti，这次需要在上面取两个点，对于任意的i点有相应后的 $i+\Delta$ 点，两条轨迹上的四个点分别记为 $P_{g,i} ,P_{g,i+\Delta}, P_{esti,i}, P_{esti,i+\Delta }$

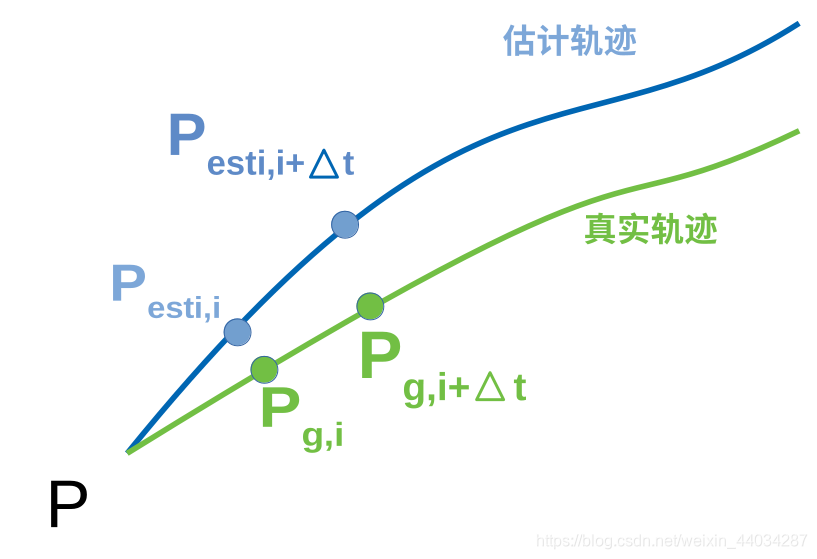
与ATE不同的是，RPE是分别计算每条轨迹上两个时刻（也就是两个点）的变化，再求这两个变化的误差。

分别求真实轨迹gi和算法估计轨迹esti的变化，还是用李代数表示：

真实轨迹上两帧之间的变化的李代数：

$E_{g,i} =log_e(T_{g,i+\Delta } / T_{g.i})^V = log_e(T_{g,i+\Delta } * T_{g.i}^{-1})^V = - log_e(T_{g.i}^{-1} *T_{g,i+\Delta })^V$

算法估计轨迹上两帧之间的变化的李代数：

$E_{esti,i} =log_e(T_{esti,i+\Delta } * T_{esti.i}^{-1})^V = - log_e(T_{esti.i}^{-1} *T_{esti,i+\Delta })^V$

最后在计算两帧之间变化的误差：

$E_i = log_e(E_{esti,i} / E_{g,i}) = log_e(E_{esti,i}*E_{g,i}^{-1}) = -log_e(E_{g,i}^{-1}*E_{esti,i})$

最后取均方根得到RPEall,注意是之前说的 $\Delta t$ 对应的是整数帧数，取均方根的时候取到 $N-\Delta t$

$RPE_{all}=\sqrt{\frac{1}{N-\Delta t}\sum _{i=1}^{N-\Delta t}||log_e((T_{gi.i}^{-1} *T_{gi,i+\Delta })^{-1}(T_{esti.i}^{-1} *T_{esti,i+\Delta })^V||_{2}^2}$

2.2平移的均方根误差

在获取平移的均方根时，不需要转换到李代数，在欧式变换（李群）中取出其平移量计算均方根。

$RPE_{trans}=\sqrt{\frac{1}{N-\Delta t}\sum _{i=1}^{N-\Delta t}||trans((T_{gi.i}^{-1} *T_{gi,i+\Delta })^{-1}(T_{esti.i}^{-1} *T_{esti,i+\Delta })||_{2}^2}$

3.代码部分

这部分引用高博《视觉slam14讲》ch4/example中的数据groundtruth.txt和estimated.txt（https://github.com/gaoxiang12/slambook2）

#include<pangolin/pangolin.h> #include <iostream> #include <sophus/se3.hpp> #include <fstream> #include <unistd.h> #include <Eigen/Core> #include <Eigen/Dense> using namespace std; using namespace Sophus; using namespace Eigen; string groundtruth_file = "/home/liao/workspace/slambook2/ch4/example/groundtruth.txt"; string estimated_file = "/home/liao/workspace/slambook2/ch4/example/estimated.txt"; typedef vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> TrajectoryType; TrajectoryType ReadTrajectory(const string& file_name); void DrawTrajectory(const TrajectoryType& gt, const TrajectoryType& esti); vector<double> calculateATE(const TrajectoryType& gt, const TrajectoryType& esti); vector<double> calculateRPE(const TrajectoryType& gt, const TrajectoryType& esti); int main(int argc, char argv) { //读取高博slam14讲中的groundtruth.txt和estimated.txt的数据 auto gi = ReadTrajectory(groundtruth_file); cout << "gi read total " << gi.size() << endl; auto esti = ReadTrajectory(estimated_file); cout << "esti read total " << esti.size() << endl; vector<double> ATE, RPE; ATE = calculateATE(gi, esti); //计算ATE RPE = calculateRPE(gi, esti); //计算RPE // DrawTrajectory(gi, esti); return 0; } vector<double> calculateATE(const TrajectoryType& gt, const TrajectoryType& esti) { double rmse_all, rmse_trans; for(size_t i = 0; i < gt.size(); i++) { //ATE旋转+平移 double error_all = (gt[i].inverse()*esti[i]).log().norm(); rmse_all += error_all * error_all; //ATE平移 double error_trans = (gt[i].inverse()*esti[i]).translation().norm(); rmse_trans += error_trans * error_trans; } rmse_all = sqrt(rmse_all / double(gt.size())); rmse_trans = sqrt(rmse_trans / double(gt.size())); vector<double> ATE; ATE.push_back(rmse_all); ATE.push_back(rmse_trans); cout << "ATE_all = " << rmse_all << " ATE_trans = " << rmse_trans << endl; } vector<double> calculateRPE(const TrajectoryType& gt, const TrajectoryType& esti) { double rmse_all, rmse_trans; double delta = 1; //delta = 2, 间隔两帧 for(size_t i = 0; i < gt.size() - delta; i++) { //RPE旋转+平移 double error_all = ((gt[i].inverse()*gt[i + delta]).inverse()*(esti[i].inverse()*esti[i + delta])).log().norm(); rmse_all += error_all * error_all; //RPE平移 double error_trans = ((gt[i].inverse()*gt[i + delta]).inverse()*(esti[i].inverse()*esti[i + delta])).translation().norm(); rmse_trans += error_trans * error_trans; } rmse_all = sqrt(rmse_all / double(gt.size())); rmse_trans = sqrt(rmse_trans / double(gt.size())); vector<double> RPE; RPE.push_back(rmse_all); RPE.push_back(rmse_trans); cout << "RPE_all = " << rmse_all << " RPE_trans = " << rmse_trans << endl; } TrajectoryType ReadTrajectory(const string& file_name) { ifstream fin(file_name); TrajectoryType trajectory; if(!fin) { cerr << "trajectory " << file_name << "not found" << endl; return trajectory; } while(!fin.eof()) { double time, tx, ty, tz, qx, qy, qz, qw; fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw; Sophus::SE3d p1(Eigen::Quaterniond(qw, qx, qy, qz), Eigen::Vector3d(tx, ty, tz)); trajectory.push_back(p1); } return trajectory; }

讯享网

讯享网//结果如下： gi read total 612 esti read total 612 ATE_all = 2.20728 ATE_trans = 0.0 RPE_all = 0.0 RPE_trans = 0.0

轨迹如图，绿色的为真实轨迹，蓝色为估算轨迹。

4.evo工具

4.1 evo工具安装以及使用说明

安装参考这个帖子：https://www.guyuehome.com/18717

evo使用看这个帖子：https://blog.csdn.net/dcq/article/details/

4.2 evo中计算ATE（APE）

evo中把ATE称为APE。

高博书中的格式是数据集TUM格式，即time, tx, ty, tz, qx, qy, qz, qw

evo中默认计算平移部分，需要通过输入-r full来改为计算平移+旋转。

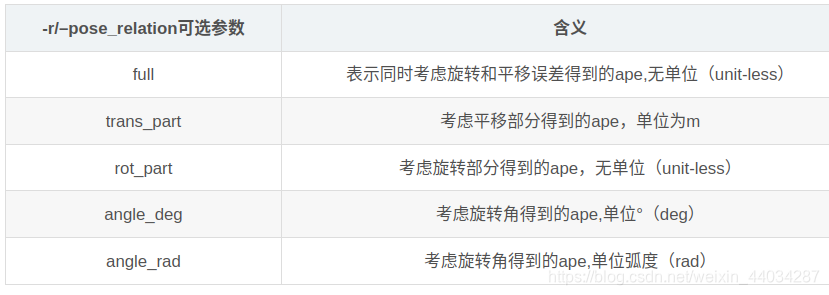
分别输入以下命令：

计算旋转+平移：rmse = 2., 自己写的是ATE_all = 2.20728

evo_ape tum -r full groundtruth.txt estimated.txt output max 2. mean 2. median 2. min 0. rmse 2. sse 3507.030550 std 0.

计算平移：rmse = 0.023082，自己写的是ATE_trans = 0.0

讯享网evo_ape tum groundtruth.txt estimated.txt output max 0.063891 mean 0.019498 median 0.016376 min 0.001271 rmse 0.023082 sse 0. std 0.012354

4.2 evo中计算RPE

默认为delta = 1的情况，如需更改为delta = 2，则： -r --delta 2，如下：

evo_rpe tum -r full --delta 2 groundtruth.txt estimated.txt

当delta = 1时，分别输入以下命令：

计算旋转+平移：rmse = 0.078218，RPE_all = 0.0

讯享网evo_rpe tum -r full groundtruth.txt estimated.txt output for delta = 1 (frames) using consecutive pairs (not aligned) max 0. mean 0.067958 median 0.063364 min 0.005507 rmse 0.078218 sse 3. std 0.038726

计算平移：rmse = 0.031082，自己写的是：RPE_trans = 0.0

evo_rpe tum groundtruth.txt estimated.txt output# for delta = 1 (frames) using consecutive pairs (not aligned) max 0. mean 0.025923 median 0.022008 min 0.000927 rmse 0.031082 sse 0. std 0.017148

最后，对比自己写的和evo算得还是有一点点差别。算旋转的时候会差0.1-0.2，算平移的时候比较准一点。

【SLAM】评估轨迹误差，手写ATE、RPE对比EVO

1.绝对轨迹误差（Absolute Trajectory Error, ATE）

1.1旋转+平移的均方根误差

1.2 仅计算平移的均方根误差

2.相对轨迹误差（Relative Pose Error, RPE）

2.1旋转+平移的均方根误差

2.2平移的均方根误差

3.代码部分

4.evo工具

4.1 evo工具安装以及使用说明

4.2 evo中计算ATE（APE）

4.2 evo中计算RPE

相关推荐