
解析:
我们先来看题目给的条件:
1) 0至4的闭区间f有定义
2) f的一次导
(a)问的是在哪个区间f是增长的,我们知道[f increasing→f'>0][f decreasing→f'<0]。所以现在用图形计算器画出f'的图像,大概找出在0至4的闭区间的范围内,f'=0和f'>0的分界点。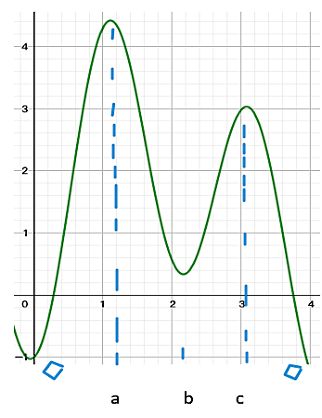

通过画图(如上图)我们得出,在大概0.282和3.758的区域内,f'>0。用到图形计算器的求解功能,我们可以较准确地算出前面的区间在保留三位小数后是(0.283,3.760)。答案就是:On the open interval between 0.283 and 3.760, f is increasing.
(b)问x是什么值时,f有局部极大值。
注意与globalmaximum 区分:一个函数可有多个local max/min,但是只可有一个global max/min。
看回刚刚用图形计算器画的图,我们知道,在(0,0.283)区间,f值减小;在(0.283,3.760)区间,f值增大;在(3.760,4)区间,f值减小。看着f'图在三个区间所包围的面积来看,在(0.283,3.760)区间包围的正面积最大,所以在当x=3.760时,f有最大值。答案就是:f has a local maxima when x=3.760
(c)问的是,在图上有几个拐点。
Inflection point就是函数改变concavity的时候:例如从concave up(f''>0)变成concave down(f''<0)。这道题只问了数量,并没有问确切的位置,所以步骤相对简便。
可以看出,在f'的x=a,x=b, 和x=c前后的地方,f''发生了变化。0到a这一段f''>0;a到b这一段f''<0;b到c这一段f''>0;c到4这一段f''<0.因为f''发生了三次变化,所以一共有三个inflection point。答案就是:f has 3 inflection points.
误区:不小心把f'的图当成了f的图像,直接找concave up/down的图
希望通过以上的练习,大家能对微积分FRQ的题目设置和易错点有了更清晰的认识。


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/43425.html