现在有一个弹珠游戏，弹珠从横坐标为S的点掉落，下方依次有n(1 <= n <= 50000)个挡板，左右端点的横坐标为l[i]和r[i] (- <= l[i] < r[i] <= ),弹珠落在挡板上你可以选择向左或者向右,直到弹珠落地，滚向位于横坐标为零的终点，请你求出弹珠水平运动的最小路程。

输入格式:

第一行输入n和s接下来n行依次为从上到下的挡板的l[i]和r[i]

输出格式:

输出弹珠水平运动的最小路程

输入样例:

在这里给出一组输入。例如：

4 0 -2 1 -1 2 -3 0 -2 1

输出样例:

在这里给出相应的输出。例如：

讯享网4

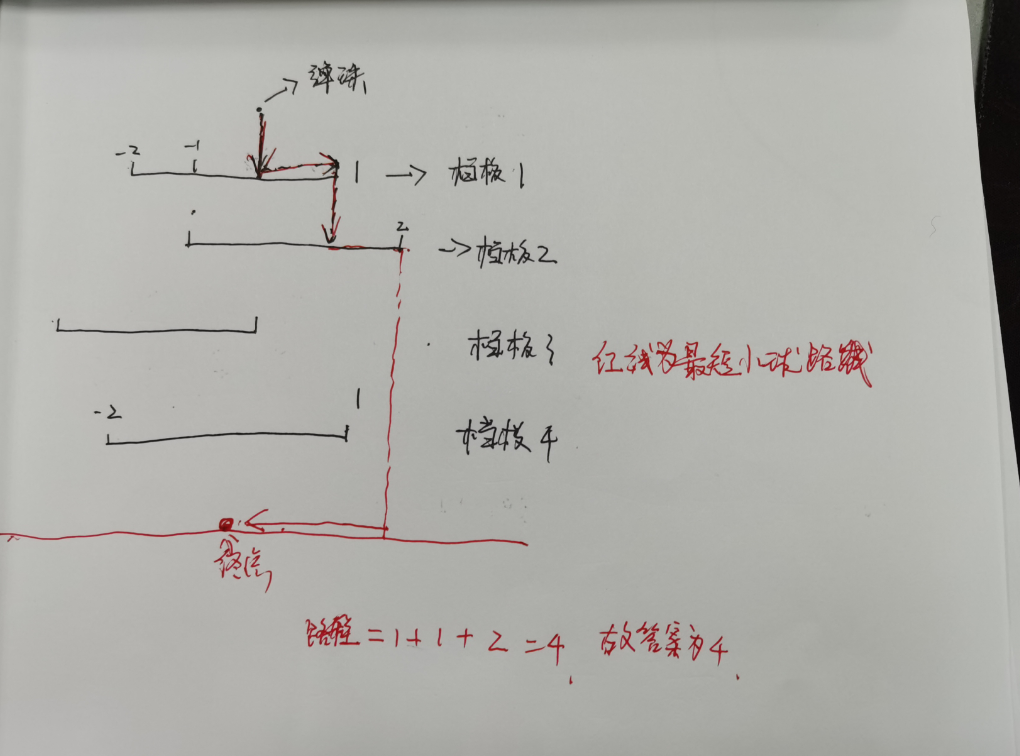
样例解释:

讯享网

思路:

作者给的时间特别充裕，足足2000ms，那不得直接dfs吗？

我们在dfs定义三个变量：

• boardIndex：表示小球第一个下方的板子的代号（不一定会落在上面）
• ballIndex：表示小球的当前坐标
• currLength：表示小球目前为止所经过的距离

那么递归过程如下所示：

1. 我们从最上面的板子A开始搜索这一次小球将落到那块板子上
   1. 如果找到了那块板子B，那么就分别讨论从这板子B的左右侧落下的情况，那么就需要使用类似min(dfs(左), dfs(右))的结构
      1. 其中如果从左出发，那么就假设小球下一次的坐标ballIndex就是板子的左端坐标，反之就是右端坐标
   2. 如果没找到板子B可以让小球落下的，就说明小球落到了地上，此时距离就是小球当前坐标到0的距离，也就是abs(ballIndex)

OK，上代码

参考代码1（普通DFS——测试点2超时）:

#include<bits/stdc++.h> using namespace std; #define lhs first #define rhs second vector<pair<int, int>> vec; int n, s; // 球的下一个挡板坐标是boardIndex，球的坐标是ballSite map<string, int> memory; int dfs(int boardIndex, int ballSite, int currLength = 0) { int i; for(i=boardIndex;i<n;++i) { if(ballSite < vec[i].rhs && ballSite > vec[i].lhs) { break; } } // 如果到底了，那么就返回这一步需要的距离 if(i == n) { return abs(ballSite) + currLength; } return min(dfs(i+1, vec[i].lhs, abs(ballSite - vec[i].lhs) + currLength), dfs(i+1, vec[i].rhs, abs(vec[i].rhs - ballSite) + currLength)); } int main() { cin>>n>>s; for(int i=0;i<n;++i) { int l, r; scanf("%d %d", &l, &r); vec.push_back({l, r}); } cout<<dfs(0, s); return 0; }

改进思路:

很不幸啊，超时了，这也难怪，有50000个板子直接上DFS属实有些侥幸。

有没有什么办法优化呢？

当然有了，DFS的优化方法就是使用记忆化搜索。记忆化搜索的条件仅需满足以下两点：

1. 不依赖任何 外部变量
2. 答案以返回值的形式存在，而不能以参数的形式存在（就是不能将 dfs 定义成 dfs(boardIndex, ballSite, currLength)，这里面的 currLength不符合要求）。
3. 对于相同一组参数，dfs 返回值总是相同的

关键在于第三点，如果是同一组参数，那么返回值相同，于是我们可以建立一个索引，将相同的【boardIndex, ballSite】组合作为key，将dfs的结果作为value，构建一个map

这里有个小技巧，由于这两个数字的范围在0~50000和-~，所以我们不如将它转换成字符串的形式存储：string key = to_string(boardIndex) + "#" + to_string(ballSite);

其中加入#意图分开两个数字，防止当100与110的组合()和1001与10的组合()发生冲突。

OK，上代码

参考代码2（记忆化DFS——测试点1段错误）：

讯享网#include<bits/stdc++.h> using namespace std; #define lhs first #define rhs second vector<pair<int, int>> vec; int n, s; // 球的下一个挡板坐标是boardIndex，球的坐标是ballSite map<string, int> memory; int dfs_memory(int boardIndex, int ballSite) { string memoryIndex = to_string(boardIndex) + "#" + to_string(ballSite); if(memory.find(memoryIndex) != memory.end()) return memory[memoryIndex]; int i; for(i=boardIndex;i<n;++i) { if(ballSite < vec[i].rhs && ballSite > vec[i].lhs) { break; } } // 如果到底了，那么就返回这一步需要的距离 if(i >= n) { return abs(ballSite); } int res = min(dfs_memory(i+1, vec[i].lhs) + abs(ballSite - vec[i].lhs), dfs_memory(i+1, vec[i].rhs) + abs(vec[i].rhs - ballSite)); memory[memoryIndex] = res; return res; } int main() { cin>>n>>s; for(int i=0;i<n;++i) { int l, r; scanf("%d %d", &l, &r); vec.push_back({l, r}); } cout<<dfs_memory(0, s); return 0; }

改进改进思路：

很过分啊！何为段错误？并不是因为数组越界，而是因为递归层数过多而导致栈溢出？？

那为什么之前的DFS没有栈溢出呢？是因为之前的DFS是尾递归，可以共用栈资源，而本记忆化DFS并不是尾递归，一个递归占用一个栈空间，所以栈资源被疯狂占用，详细可以看这篇文章，了解一下尾递归和普通递归的区别：《递归和尾递归的区别和原理》

这就很难受了，每次与胜利之差一步之遥。

行吧，既然递归不行，改成循坏可否？

我们使用的是记忆化搜索，说白了就是动态规划的递归写法。

仔细观察dfs_memory，答案是从里往外逐渐扩散的，那么我们每次知道最下面的板子的最优解，依次往上找当前板子的最优解。

这里有点不太直观，不妨假设板子的左右两端就是小球的起始落点，那么分别落下去碰到的第一个板子，比较从左走还是从右走最短。

因为是从下往上找板子的最优解，所以不需要再考虑落下去碰到板子后，再往后的情况了，因为已经有最优解了。（就是记忆化的原型，存储已经搜索过的最优解）

OK，上代码

参考代码3（动态规划——AC）:

其中dp[i][0]表示第i个板子从左走的最优解，dp[i][1]表示第i个板子从右走的最优解。

#include<bits/stdc++.h> using namespace std; #define lhs first #define rhs second vector<pair<int, int>> vec; int n, s; int solution() { int dp = new int*[n+1]; for(int i=0;i<=n;++i) { dp[i] = new int[2]; } // 0左1右 dp[n-1][0] = abs(vec[n-1].lhs); dp[n-1][1] = abs(vec[n-1].rhs); for(int i=n-2;i>=0;--i) { int j; // 小球从第i个板的左边落下，找到小球能落到的第一个板子，考虑从这个板子左右走哪个是最优解 for(j=i+1;j<n;++j) { if(vec[i].lhs < vec[j].rhs && vec[i].lhs > vec[j].lhs) { dp[i][0] = min(dp[j][0] + abs(vec[i].lhs - vec[j].lhs), dp[j][1] + abs(vec[i].lhs - vec[j].rhs)); break; } } if(j == n) { dp[i][0] = abs(vec[i].lhs); } // 小球从第i个板的右边落下，找到小球能落到的第一个板子，考虑从这个板子左右走哪个是最优解 for(j=i+1;j<n;++j) { if(vec[i].rhs < vec[j].rhs && vec[i].rhs > vec[j].lhs) { dp[i][1] = min(dp[j][0] + abs(vec[i].rhs - vec[j].lhs), dp[j][1] + abs(vec[i].rhs - vec[j].rhs)); break; } } if(j == n) { dp[i][1] = abs(vec[i].rhs); } } for(int i=0;i<n;++i) { if(s < vec[i].rhs && s > vec[i].lhs) { return min(dp[i][0] + abs(vec[i].lhs - s), dp[i][1] + abs(vec[i].rhs - s)); } } return s; } int main() { cin>>n>>s; for(int i=0;i<n;++i) { int l, r; scanf("%d %d", &l, &r); vec.push_back({l, r}); } cout<<solution(); return 0; }