2025年《阵列信号处理及MATLAB实现》阵列响应矩阵(均匀线阵、均匀圆阵、L型阵列、平面阵列和任意阵列)

大家好，我是讯享网，很高兴认识大家。

2.7 阵列响应矢量/矩阵

常用的阵列形式包括均匀线阵、均匀圆阵、L型阵列、平面阵列和任意阵列等。

1、均匀线阵

讯享网

假设接收信号满足窄带条件，即信号经过阵列长度所需的时间应远远小于信号的相干时间，信号包络在天线阵列传播时间内变化不大。为简化，假定信源和天线阵列是在同一平面内，并且入射到阵列为平面波。

来波方向为 $\theta_K(k=1,2,...,K)$

一共有个阵元

则阵元间距为的均匀线阵的阵列响应矢量为：

$\vec a(\theta)=\begin{bmatrix} 1 &exp(-j2\pi \frac{d}{\lambda}sin\theta_k) &... & exp(-j2\pi(M-1) \frac{d}{\lambda}sin\theta_k) \end{bmatrix}^T$

定义方向矩阵为： $A=[\vec a(\theta_1),\vec a(\theta_2),...,\vec a(\theta_k)]=\begin{bmatrix} 1 &1 &1 &1 \\ e^{-j\frac{2\pi d}{\lambda}sin\theta_1}& e^{-j\frac{2\pi d}{\lambda}sin\theta_2} & ... & e^{-j\frac{2\pi d}{\lambda}sin\theta_k}\\ ... & ... & ... &... \\ e^{-j\frac{2\pi d}{\lambda}(M-1)sin\theta_1} &e^{-j\frac{2\pi d}{\lambda}(M-1)sin\theta_2} &... & e^{-j\frac{2\pi d}{\lambda}(M-1)sin\theta_k} \end{bmatrix}$

2、均匀圆阵

均匀圆形的M个相同的全向阵列均匀分布在平面x-y上一个半径为R的圆周上，如图所示。

采用球面坐标系表示入射平面波的波达方向，坐标系的原点O在阵列的中心。信源的仰角 $\theta$ 是原点到信源的连线与z轴之间的夹角，方位角 $\phi$ 则是原点到信源的连线在平面x-y的投影与x轴之间的夹角。

方向矢量 $\vec a(\theta,\phi)$ 是DOA为 $(\theta,\phi)$ 的阵列响应， $\vec a(\theta,\phi)$ 可表示为：

$\vec a(\theta,\phi)=\begin{bmatrix} exp(j2\pi Rsin\theta cos(\phi-\gamma_0)/ \lambda\\ exp(j2\pi Rsin\theta cos(\phi-\gamma_1)/ \lambda\\ ...\\ exp(j2\pi Rsin\theta cos(\phi-\gamma_{M-1})/ \lambda \end{bmatrix}$

其中， $\gamma_m = 2\pi m/M,m=0,1,...,M-1$ ，为半径

3、L型阵列

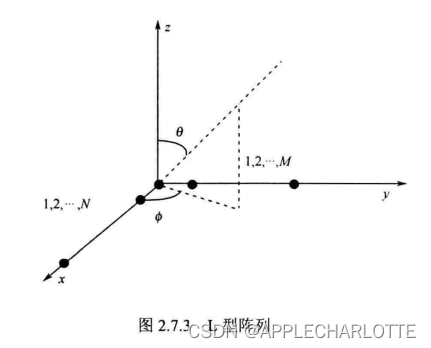
L型阵列由x轴上阵元数为N的均匀线阵和y轴上阵元数为M的均匀线阵组成，一个有M+N-1个阵元。阵元间距为d。

假设空间有K个信源照射到阵列上，其二维波达方向为 $(\theta_k,\phi_k),k=1,2,...,K$

其中 $\theta_k$ 和 $\phi_k$ 分别代表第k个信源的仰角和方位角。

假设入射到此阵列上的信源数为K，则x轴上N个阵元对应的方向矩阵为

$A_x=\begin{bmatrix} 1 &1 &1 &1 \\ e^{j2\pi dcos\phi_1 sin\theta_1/\lambda}& e^{j2\pi dcos\phi_2 sin\theta_2/\lambda}& ...& e^{j2\pi dcos\phi_k sin\theta_k/\lambda}\\ ...& ... & ... &... \\ e^{j2\pi d(N-1)cos\phi_1 sin\theta_1/\lambda} & e^{j2\pi d(N-1)cos\phi_2 sin\theta_2/\lambda} & ...& e^{j2\pi d(N-1)cos\phi_k sin\theta_k/\lambda} \end{bmatrix}$

y轴上M个阵元对应的方向矩阵为：

$A_y=\begin{bmatrix} 1 &1 &1 &1 \\ e^{j2\pi dsin\phi_1 sin\theta_1/\lambda}& e^{j2\pi dsin\phi_2 sin\theta_2/\lambda}& ...& e^{j2\pi dsin\phi_k sin\theta_k/\lambda}\\ ...& ... & ... &... \\ e^{j2\pi d(M-1)sin\phi_1 sin\theta_1/\lambda} & e^{j2\pi d(M-1)sin\phi_2 sin\theta_2/\lambda} & ...& e^{j2\pi d(M-1)sin\phi_k sin\theta_k/\lambda} \end{bmatrix}$

其中 A_x 和 A_y 均为范德蒙德矩阵。

4、平面阵列

设平面阵列的阵元数为M*N，信源数为K。

其中 $\theta_k$ 和 $\phi_k$ 分别代表第k个信源的仰角和方位角。

则空间的第i个阵元与参考阵元之间的波程差为：

$\beta = 2\pi(x_icos\phi sin\theta+y_isin\phi cos\theta+z_icos\theta)/\lambda$

式中， (x_i,y_i) 为第i个阵元的坐标，面阵一般在x-y面内，所以 z_i 一般为0

由上面L型阵列的分析可知，x轴上的N个阵元的方向为 A_x ，y轴上的M个阵元的方向为 A_y 。所以如上图所示的子阵1的方向矩阵为 A_x ，而子阵2的方向矩阵就需要考虑沿y轴的偏移，每个阵元相对于参考阵元的波程差就等于子阵1的阵元的波程差加上 $2\pi dsin\phi sin\theta/\lambda$ ，所以可得：

子阵1： A_1 = A_xD_1(A_y)

子阵2： A_2 = A_xD_2(A_y)

......

子阵M： A_M = A_xD_M(A_y)

其中， $D_m(\cdot )$ 是由矩阵的m行构造的一个对角矩阵。

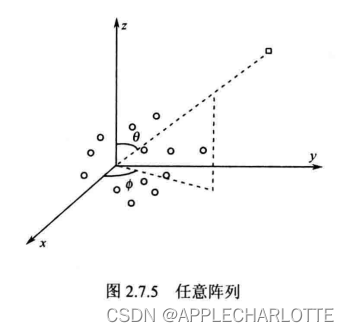
5、任意阵列

假设M元阵列位于任意三维空间中，如图所示。定义阵列中第m个传感器为 r_m=(x_m,y_m,z_m) 。方向矩阵是：

$A=[\vec a(\theta_1,\phi_1),\vec a(\theta_2,\phi_2),...,\vec a(\theta_k,\phi_k)]\in\mathbb{C}^{M\times K}$

其中， $\vec a(\theta_k,\phi_k)$ 是第k个信源的方向矢量，可以表示为：

$\vec a(\theta_k,\phi_k)=\begin{bmatrix} 1\\ e^{j2\pi(x_2sin\theta_kcos\phi_k+y_2sin\theta_ksin\phi_k+z_2cos\theta_k)/\lambda}\\ ... \\ e^{j2\pi(x_Msin\theta_kcos\phi_k+y_Msin\theta_ksin\phi_k+z_Mcos\theta_k)/\lambda} \end{bmatrix}\in\mathbb{C}^{M\times1}$

其中 $\lambda$ 是波长。