【n个节点的二叉树有多少种形态(Catalan数)】
(2)如果有两个节点呢?我们很自然想到,应该在f(1)的基础上考虑递推关系。那么,如果固定一个节点后,左右子树的分布情况为1=1+0=0+1,故有f(2) = f(1) + f(1)
(4)那么有n个节点呢?我们固定一个节点,那么左右子树的分布情况为n-1=n-1 + 0 = n-2 + 1 = … = 1 + n-2 = 0 + n-1。此时递归表达式为f(n) = f(n-1) + f(n-2)f(1) + f(n-3)f(2) + … + f(1)f(n-2) + f(n-1)
接下来我们定义没有节点的情况,此时也只有一种情况,即f(0)=1
那么则有:
f(0)=1,f(1)=1
f(2)=f(1)f(0)+f(0)f(1)
f(3)=f(2)f(0)+f(1)f(1)+f(0)f(2)
.
.
.
.
f(n)=f(n-1)f(0)+f(n-2)f(1)+……….+f(1)f(n-2)+f(0)f(n-1)
该数列称为卡特兰数(Catalan数),该递推关系的解为:
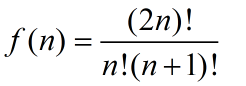
即含n个节点的二叉树有f(n)种形态。
【其他使用Catalan数解决的问题】
(1)矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
(2)一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
(3)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
(4)将一个凸多边形区域分成三角形区域的方法数?
(5)在圆上选择2n个点,将这些点成对连接起来,使得所得到的n条线段不相交的方法数。
(6)一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
本文由http://www.cnblogs.com/ShaneZhang/p/4102581.html以及http://www.cppblog.com/MiYu/archive/2010/08/07/122573.html总结而成


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/63979.html