偏最小二乘回归(partial least squares regression, 也称PLS)是一个 与主成分分析回归(principal components regression)有关系的统计方法。不是找到自变量和因变量之间的最大方差的超平面,而是找到一个能将预测变量和可观测变量投影到新空间的线性回归模型 (wikipedia, 2020)
先从Penalised Loss说起
Penalised Loss = Original loss + Penalty
Original loss = MSE
Panelty = λ \lambda λ * // β \beta β//
lamda变大–>panelty变大–> penalised loss变大–>Original loss变小–>容易overfit
经典的penalize loss图
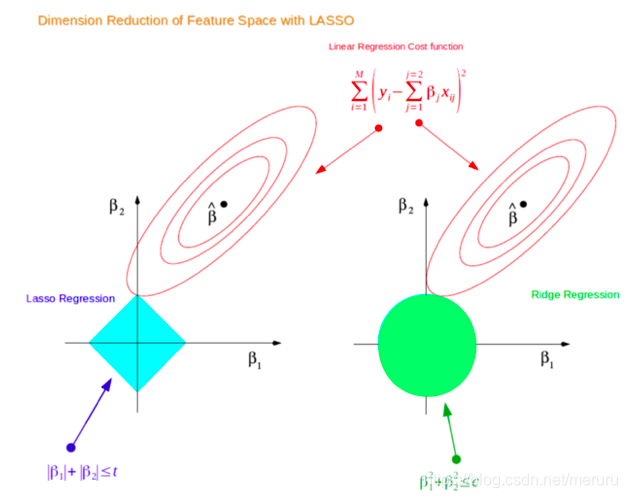
这图的目的是求出使Penalty loss最小的beta
左边的是lasso penalty= / / β 1 / / + / / β 2 / / //\beta_1// + //\beta_2// //β1//+//β2// 所以中间图像为方形
右边的是ridge penalty= / / β 1 / / 2 + / / β 2 / / 2 //\beta_1//^2+ //\beta_2//^2 //β1//2+//β2//2 所以中间图像为圆形
中间实心区域为指定 λ \lambda λ时的penalty,面积越大,penalty越小。
红色圈为MSE,中间的点为MSE最小时 β 1 \beta_1 β1, β 2 \beta_2 β2的值,同一个圈上MSE值相同。
calibration即为调参,指在该 λ \lambda λ下的 o p t ( M S E ) _{opt}(MSE) opt(MSE)。
由此,最优penalize loss时 β \beta β的取值即为红色圈与蓝**域相交的部分。因为这是constrianed penalize,所以不能超过蓝**域。
此图为二维,用于确定只有两个 β \beta


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/58967.html