大家好，我是讯享网，很高兴认识大家。

推荐速成课程：

讯享网

地址

bilibili.com/video/BV1z84y1z7Vp

点我进入

适用人群
期末突击,二级+期末+考研+学习数据结构打基础,考前复习数据结构,巩固数据结构基础 的宝贝

学习步骤：
每一章，都会先讲基础，然后下一节就是配套习题讲解， 坚持学完全部章即可 拿捏期末,

同时在课程最后提供一个新的整套题的讲解，进行巩固拔高

1 时间和空间 复杂度

助记:

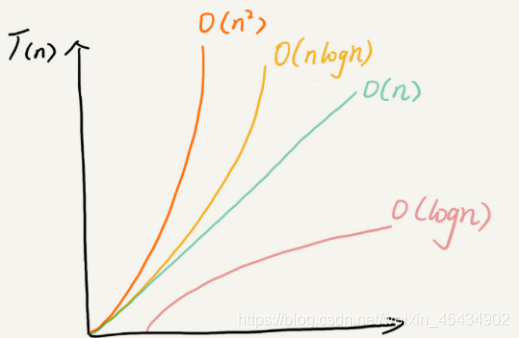
2 线性表-顺序存储结构

3 线性表-链式存储结构(单链表)

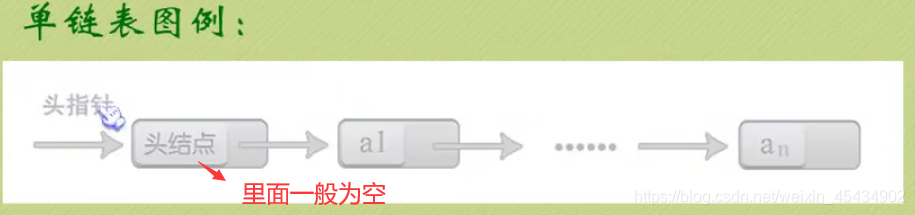
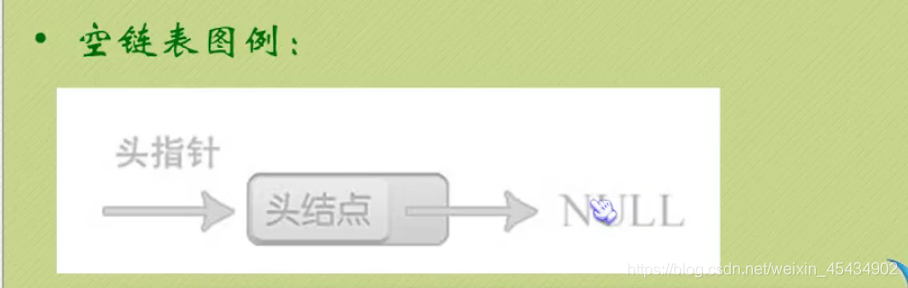
p->data(表示ai) :指向线性表的第 i 个元素的指针
p->next->data(表示ai+1) :指向第 i+1 个元素

(上面有个小错误 ) j<i 在第三行





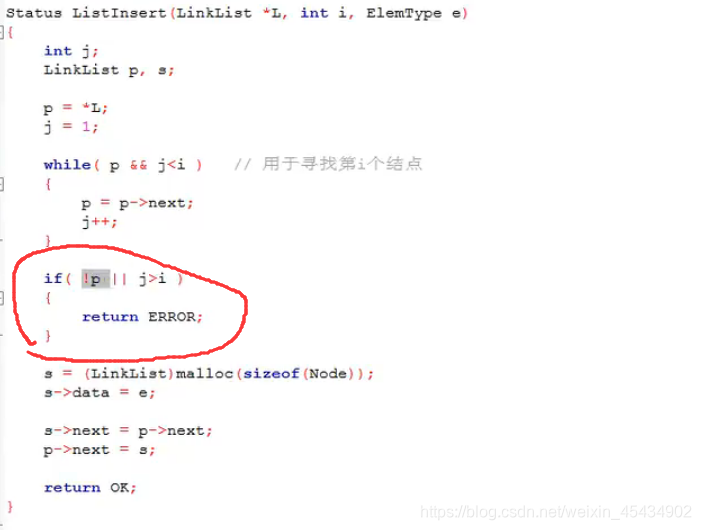
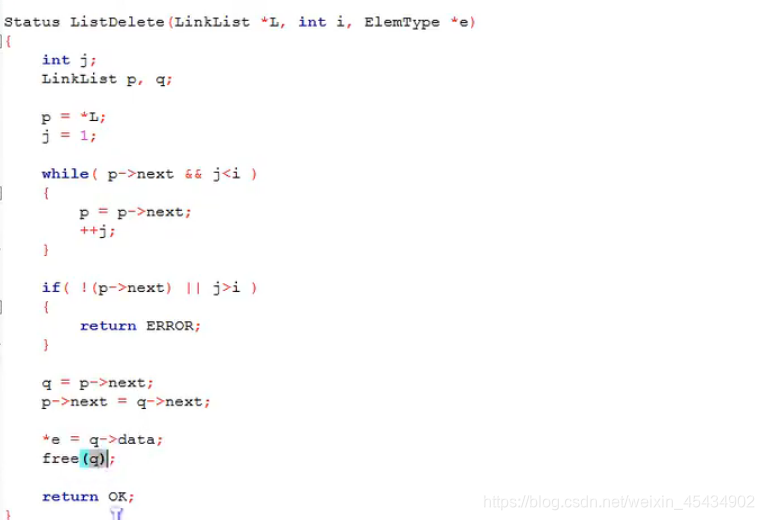
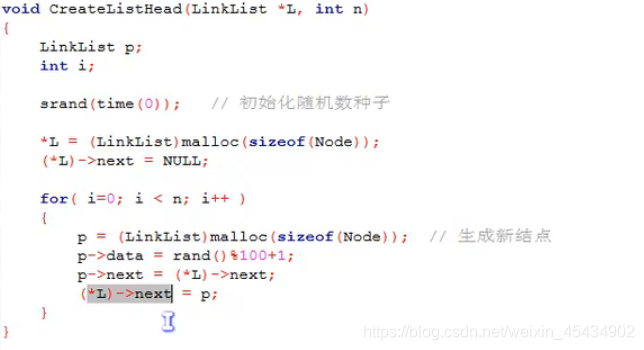
头插法 生成的链表中,结点的次序和输入的顺序相反。

尾插法

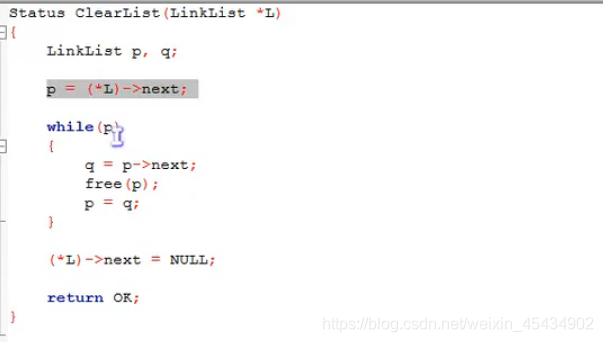
4 线性表-链式存储结构(静态链表)

静态链表 : 古人用 数组 来描述的 链表

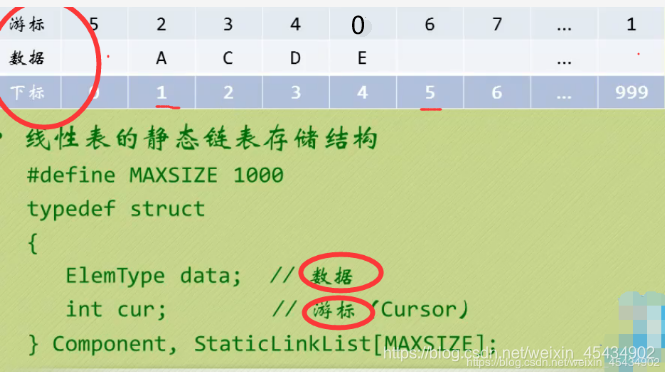
第一个数组:
指向备用链表的下表

最后一个数组:
指向第一个有数值的结点的地址

在静态链表L中第 i 个元素之 前 插入 新的数据元素e

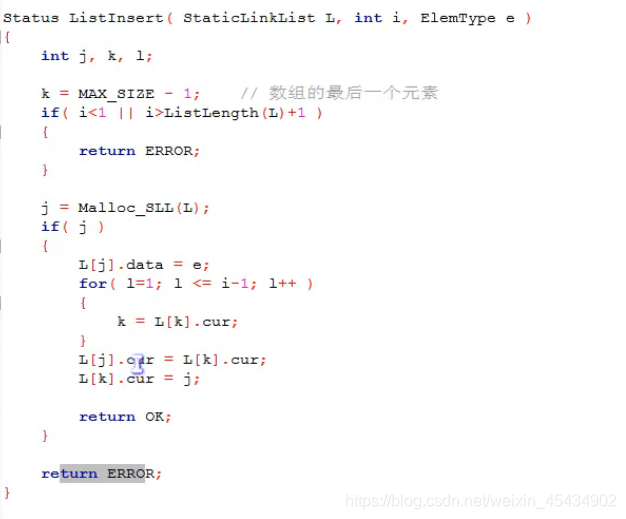
删除静态链表:

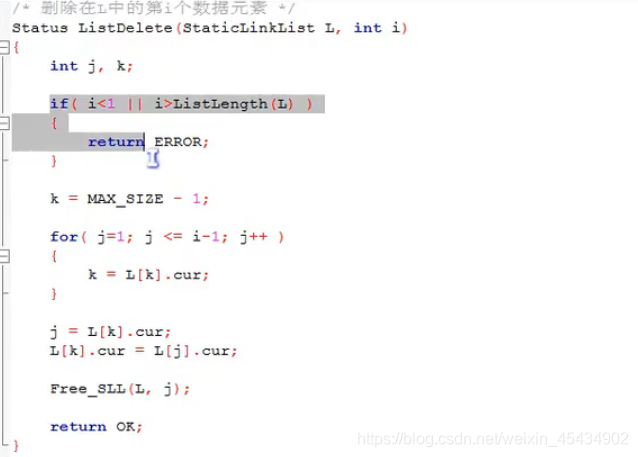
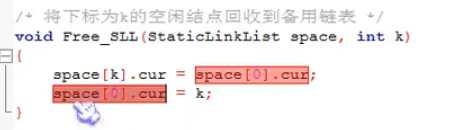
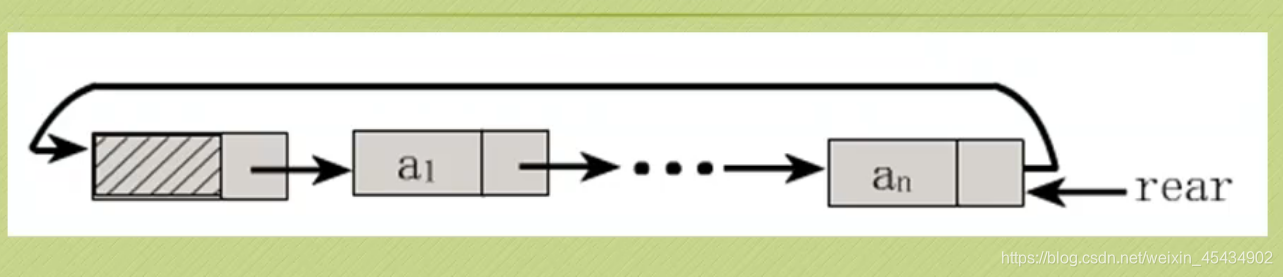
5 线性表-链式存储结构(循环链表)

尾指针: rear表示
初始化:

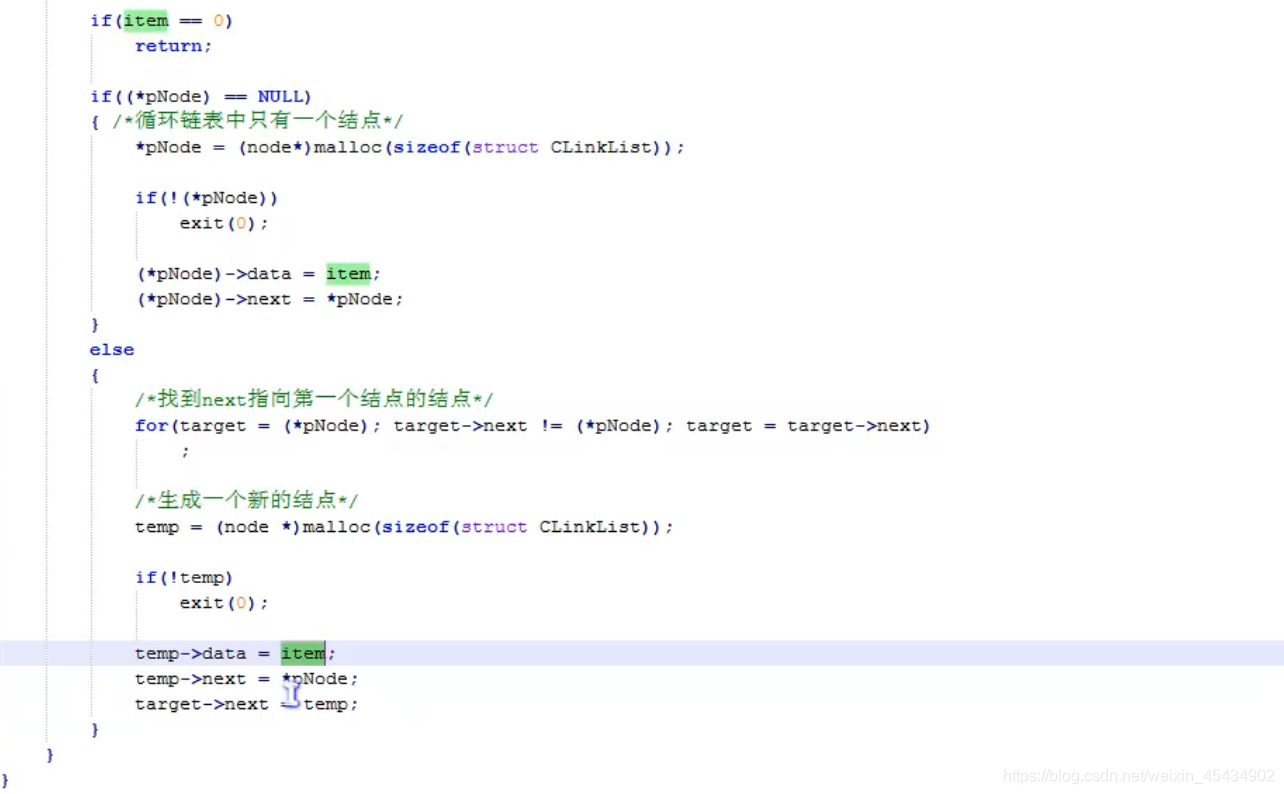
插入:


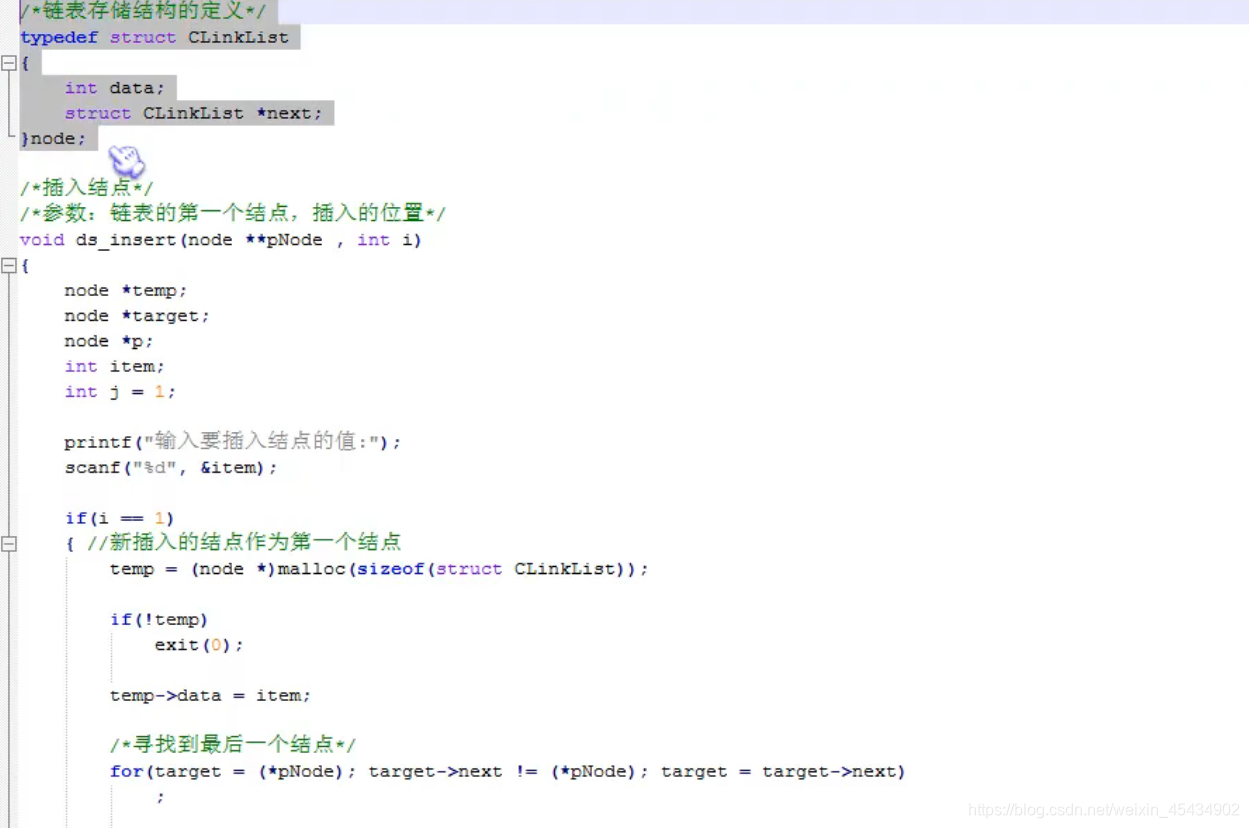
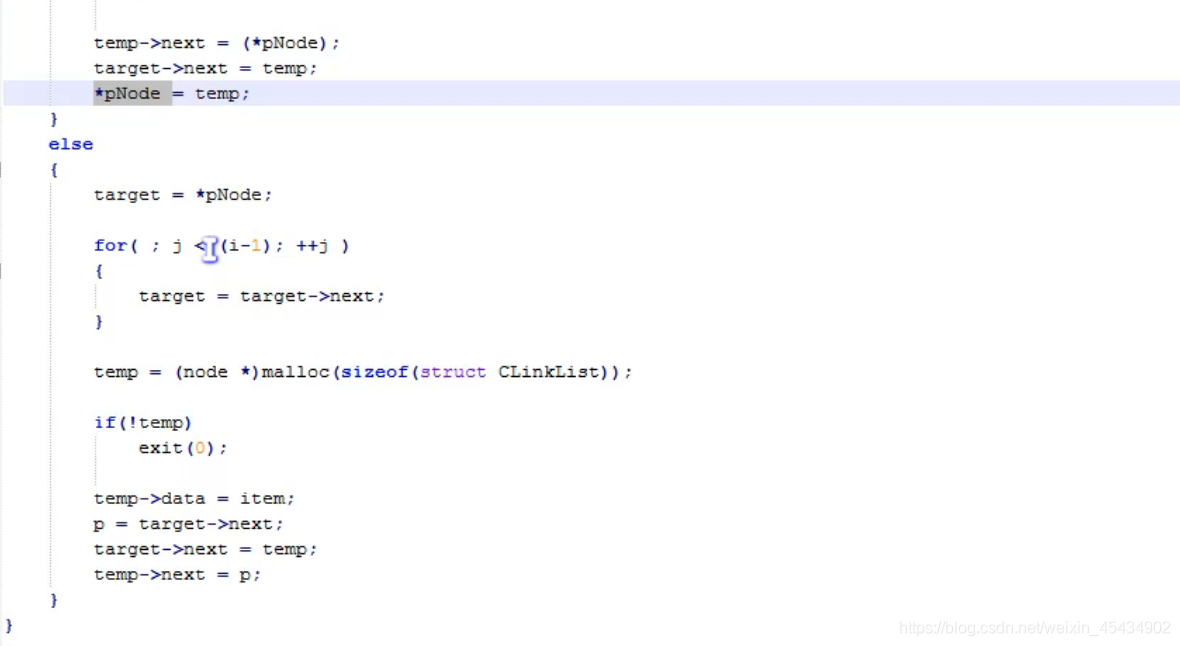
删除:

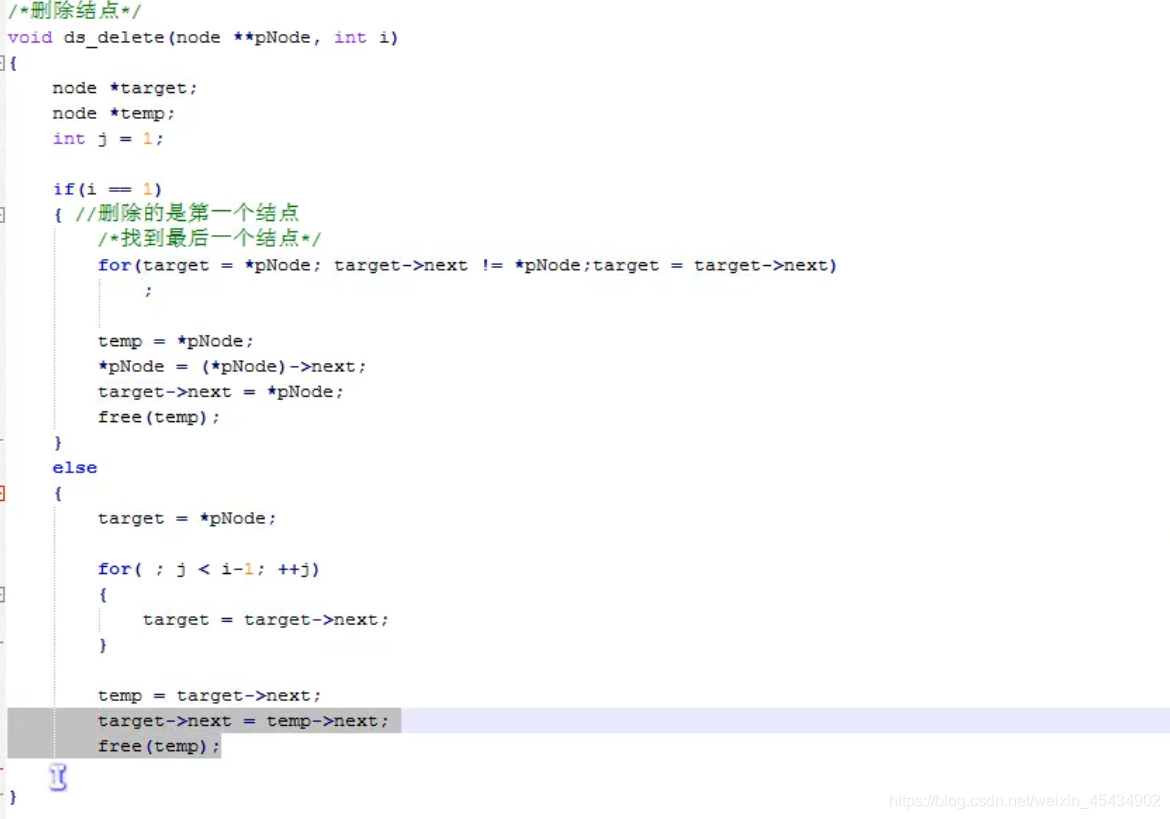
查找:

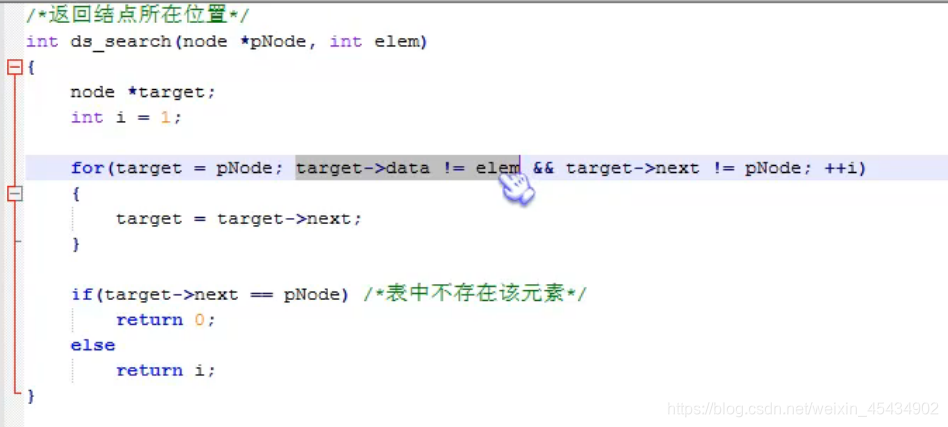
线性表里面 从1开始 序号1 代表第一个元素

特点:



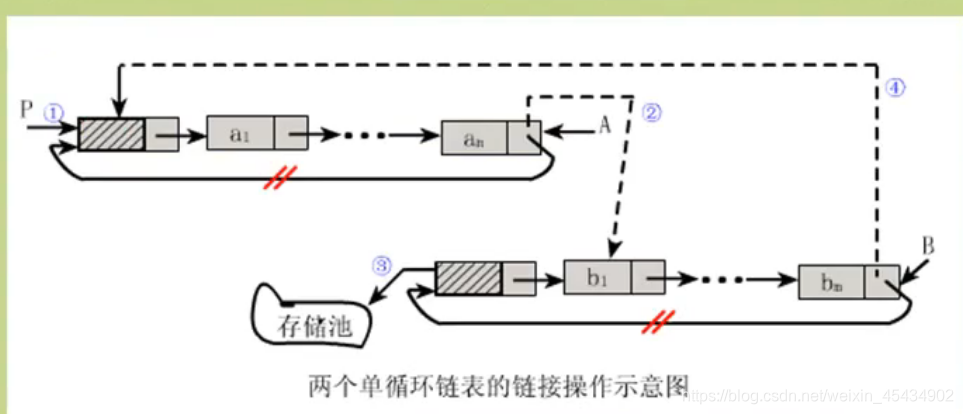
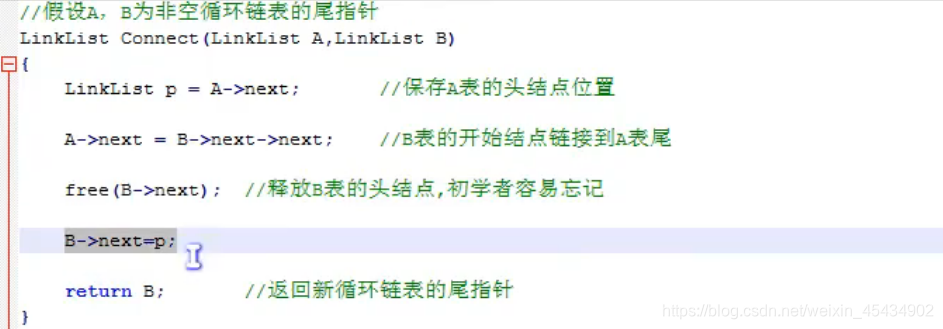
判断其中是否有环

拉丁方阵的代码展示

 #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #define OK 1 #define ERROR 0 typedef struct Node { 
    int data; struct Node* next; } Node, *LinkList; /* 创建循环链表 */ int CreatCircleList(Node** circle_list,int n) { 
    printf("请输入%d个不同的数字：",n); int i = 0; //创建头结点 Node* head = (Node*)malloc(sizeof(Node)); Node* temp = head;//temp 移动指针，刚开始指向头结点 while (i < n) { 
    int data=0; scanf("%d",&data); //创建结点并初始化数据 Node* node = (Node*)malloc(sizeof(Node)); node->data = data; node->next = NULL; //将结点添加到循环链表中 temp->next = node; temp = node; i++; } //循环结束 temp指向最后一个结点,让其指向第一个结点，形参循环列表 temp->next = head->next; //循环链表指向第一个结点 *circle_list = head->next; //释放头结点 free(head); return OK; } //获取循环链表长度 int LengthCircleList(Node* circle_list) { 
    if (circle_list == NULL) { 
    return 0; } int i = 1; Node* node = circle_list;//node为移动指针，node 开始指向循环链表第一个结点 //循环链表遍历完判断，尾结点的指针域指向第一个结点 while (node->next != circle_list) { 
    node = node->next; i++; } return i; } /* 显示拉丁方阵 */ int ShowLatin(Node* latin_list) { 
    int len = LengthCircleList(latin_list); Node* first = latin_list; for (size_t i = 0; i < len; i++) { 
    Node* node = first; int j = 0; /* 找到开始结点 第一行 开始结点为 循环链表第1个位置结点 第二行 开始结点为 循环链表第2个位置结点 第N 行 开始结点为 循环链表第n个位置结点 */ while(j < i) { 
    node = node->next; j++; } Node * begin = node; int k = 0; //遍历完这个循环列表 while(k<len) { 
    printf("%d\t",begin->data); begin = begin->next; k++; } printf("\n"); } return OK; } //销毁链表释放内存 int DestroyCricleList(Node* circle_list) { 
    if (circle_list == NULL) { 
    return ERROR; } Node* node = circle_list;//node为移动指针，node 开始指向循环链表第一个结点 //循环链表遍历完判断，尾结点的指针域指向第一个结点 while (node->next!= circle_list) { 
    Node* temp = node; node = node->next; free(temp); } //释放最后一个结点 free(node); return OK; } int main(int argc, char *argv[]) { 
    Node* circle_list = NULL; while (1) { 
    printf("请输入拉丁方阵的阶数(0退出)："); int n = 0; scanf("%d", &n); if (n == 0) { 
    break; } CreatCircleList(&circle_list,n); ShowLatin(circle_list); DestroyCricleList(circle_list); } circle_list = NULL; return 0; } 

讯享网

6 线性表-链式存储结构(双向链表)

双向链表的插入:

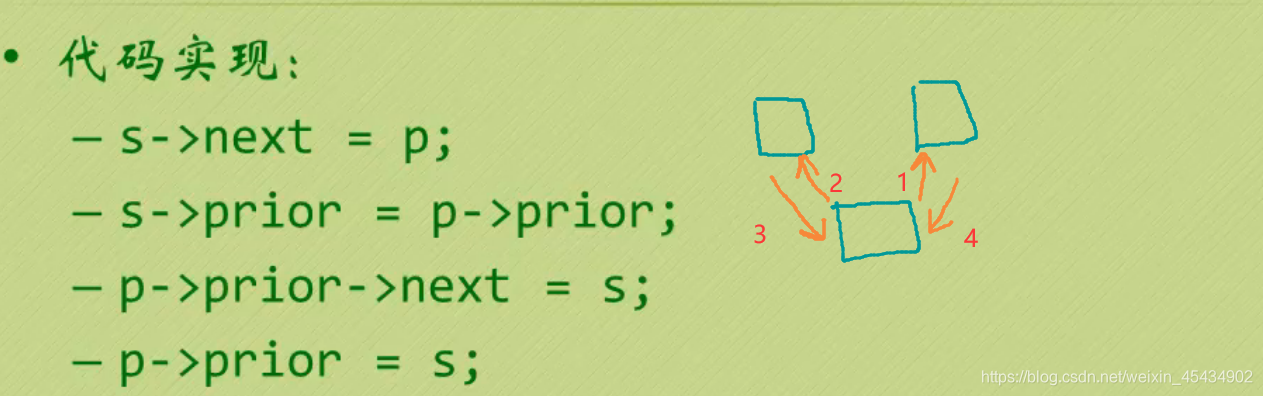
双向链表的删除:

7 栈和队列(顺序存储结构)

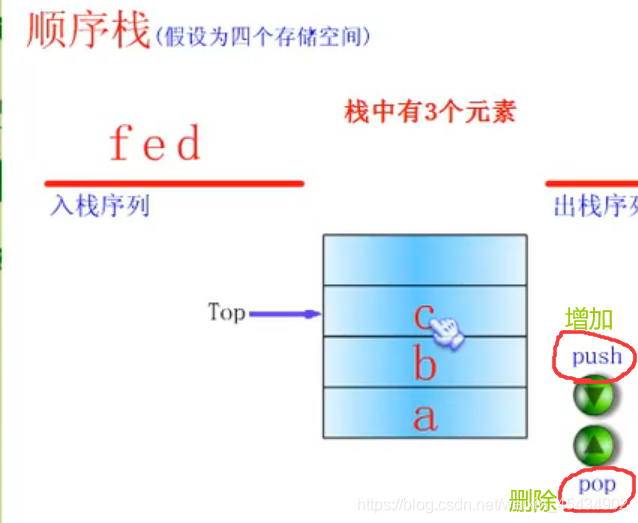
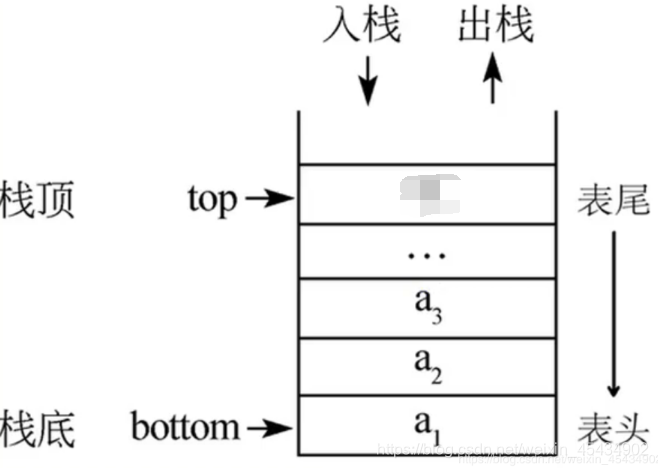
typedef int elemtype





出栈操作:

*e 是显示已经删除的元素

#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10

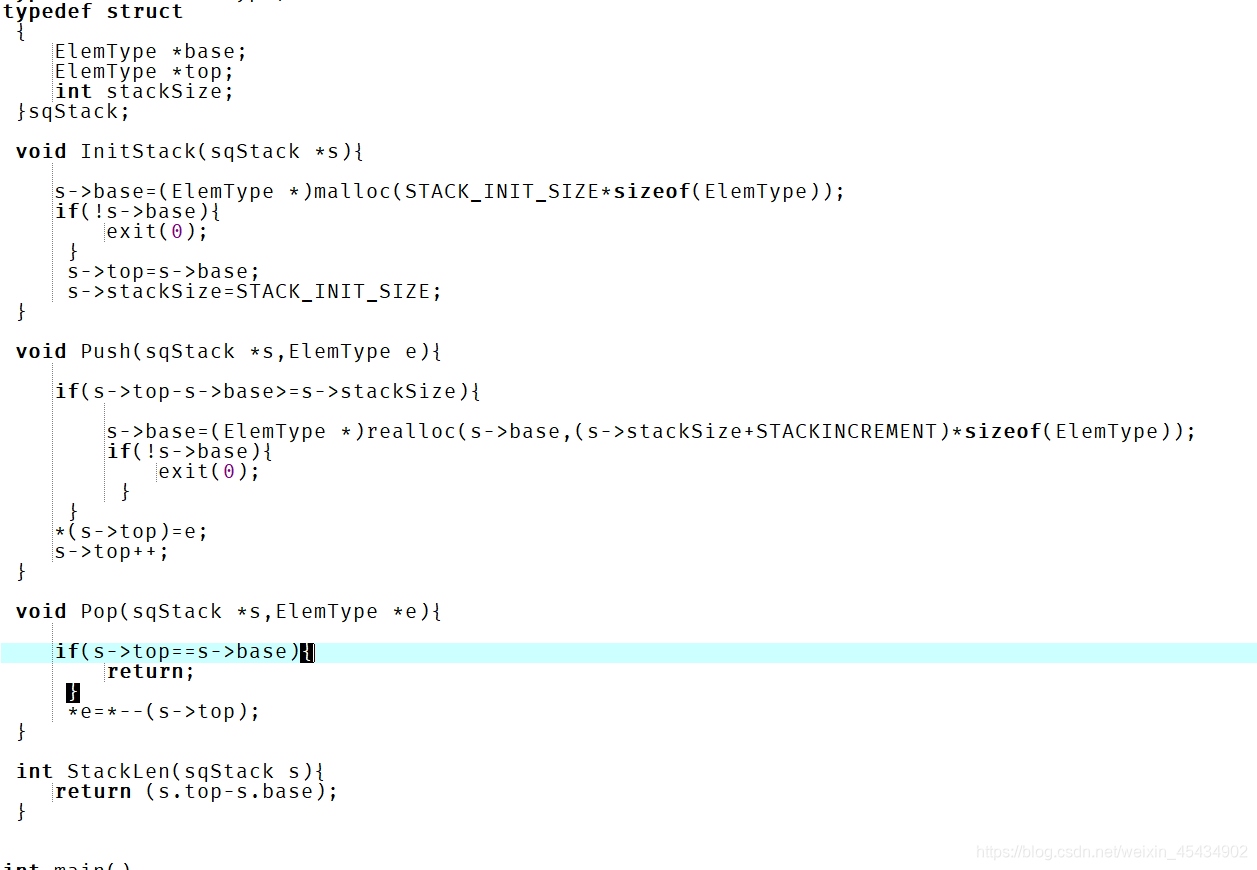
8 栈和队列(链式存储结构)

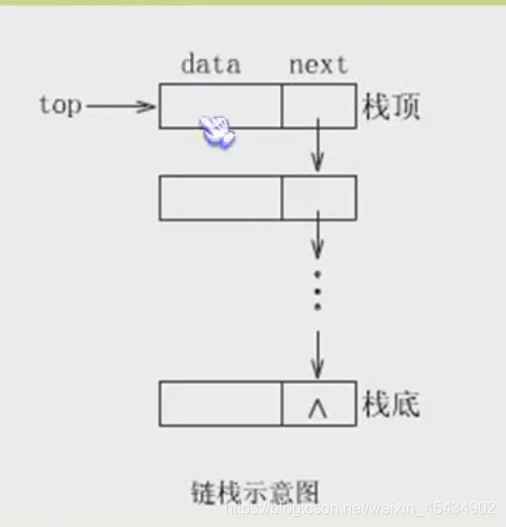
队列的链式存储结构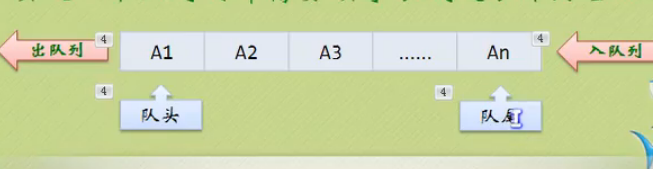

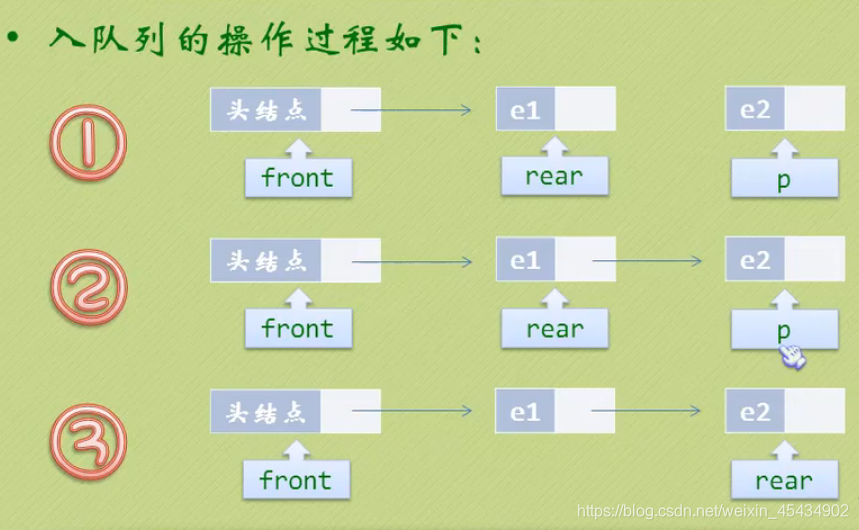
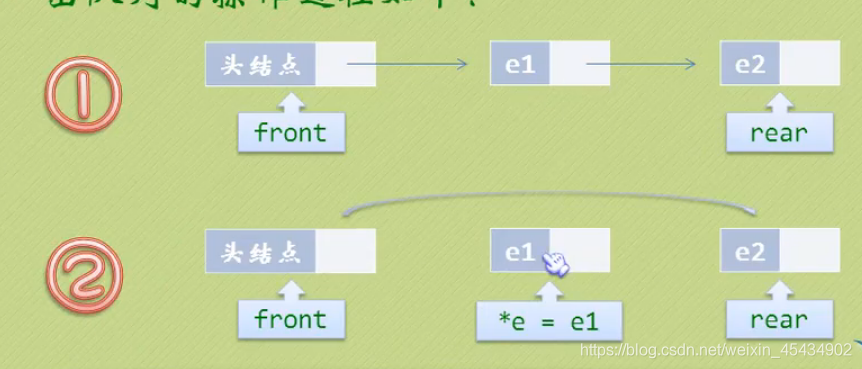
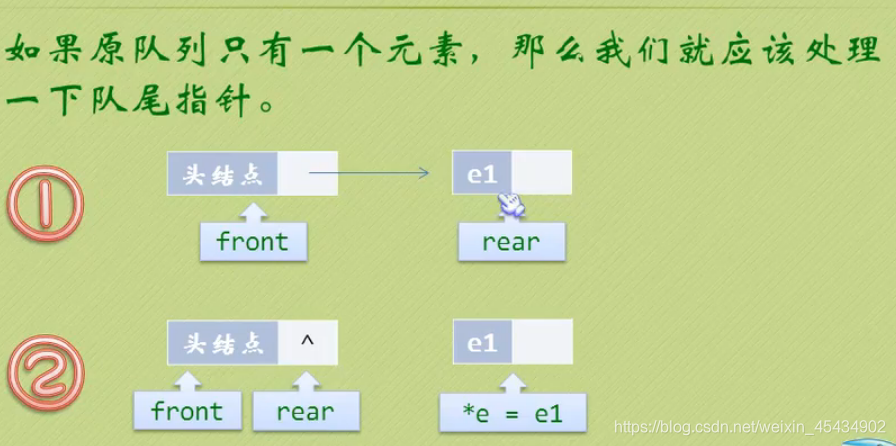
队列的顺序存储结构(循环队列)
定义一个循环队列:

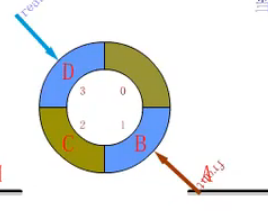
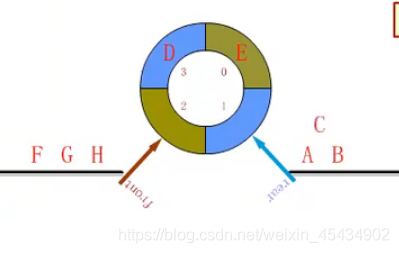
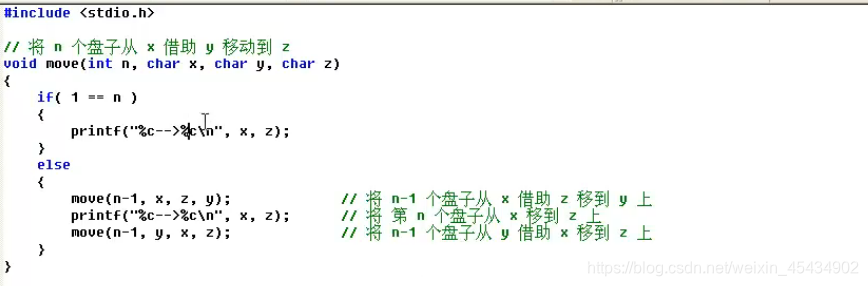
9 递归和分治思想

递归:

10 KMP算法

原理代码分析: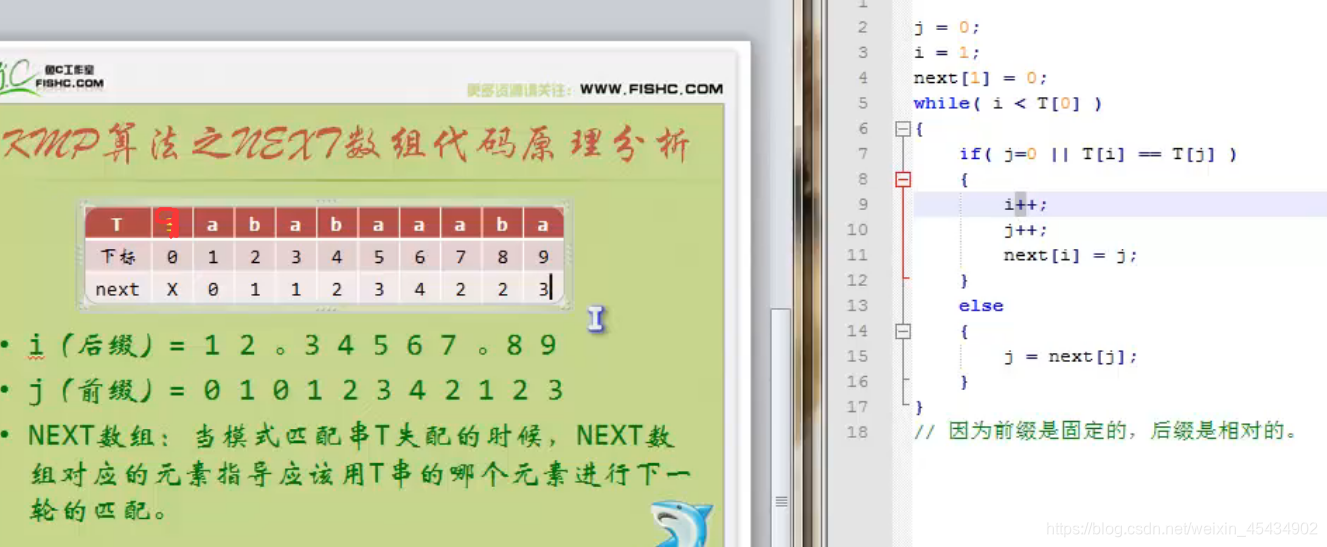
j==0(错误)
KMP算法的最终实现(优化版)

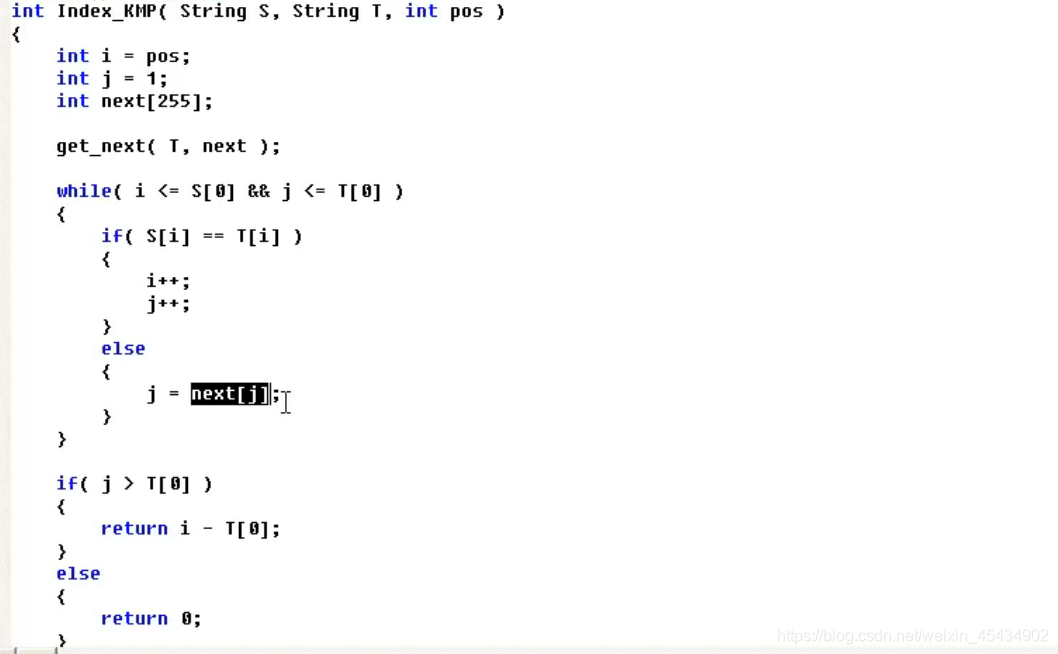
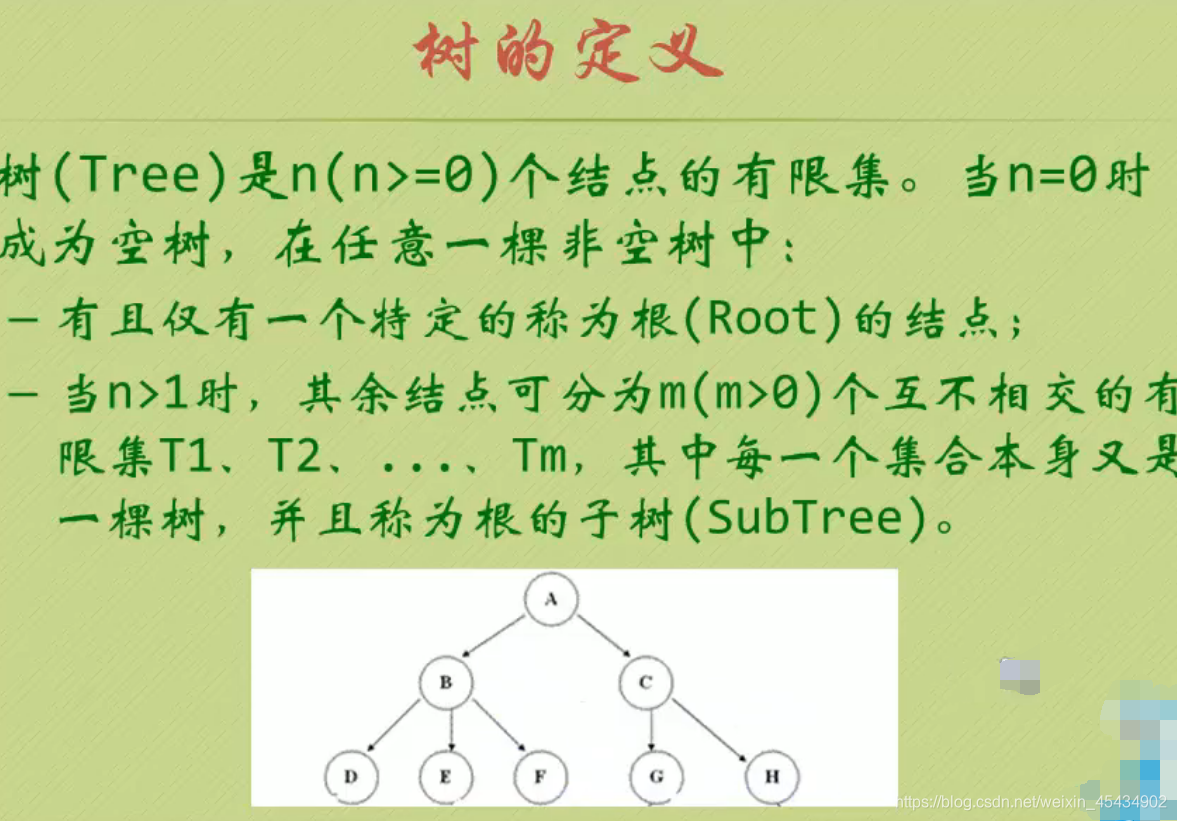
11 树

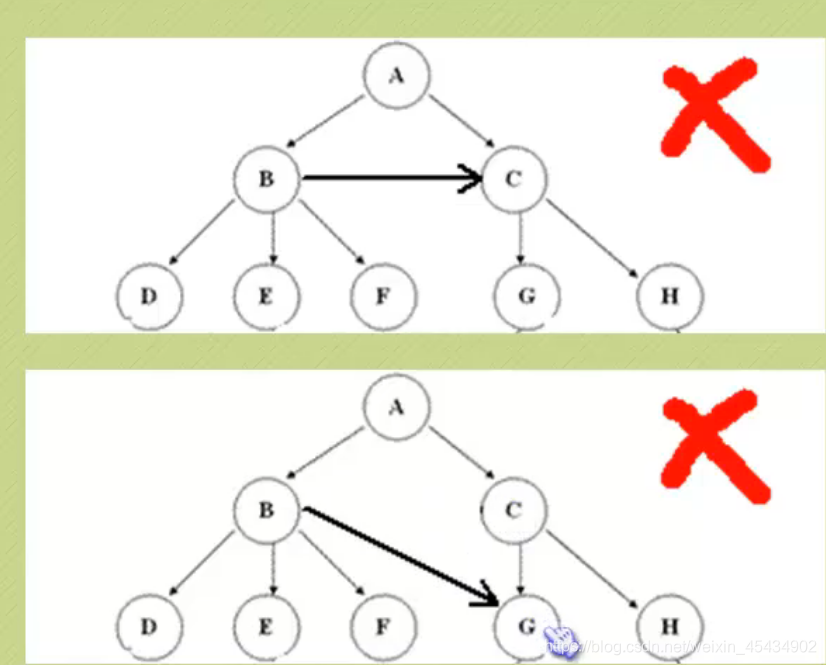
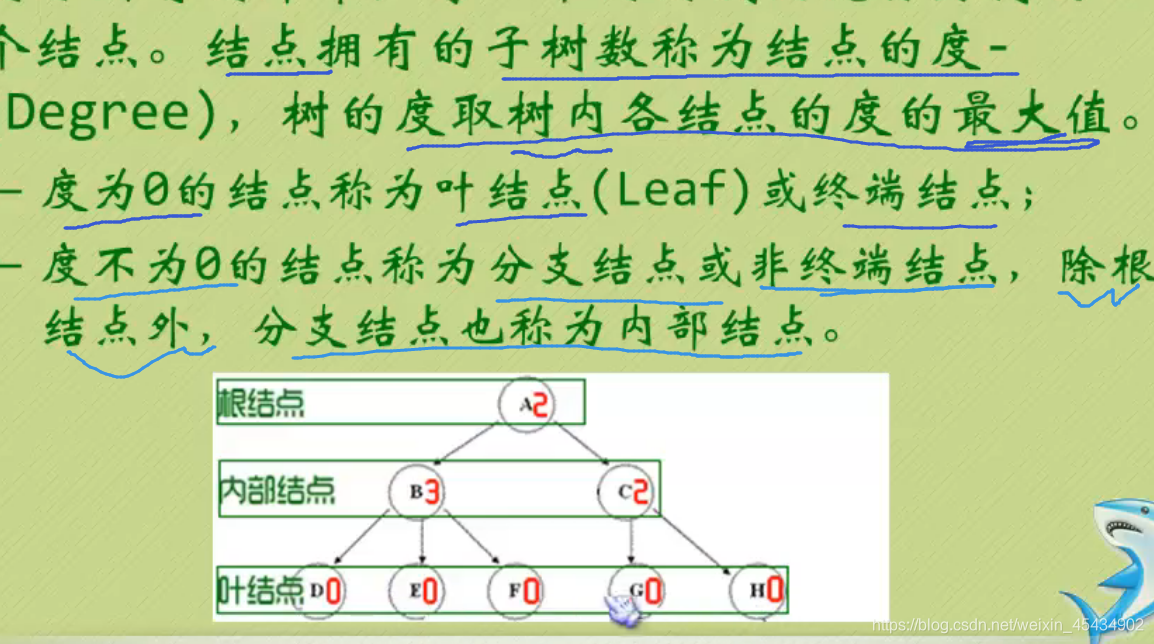
度

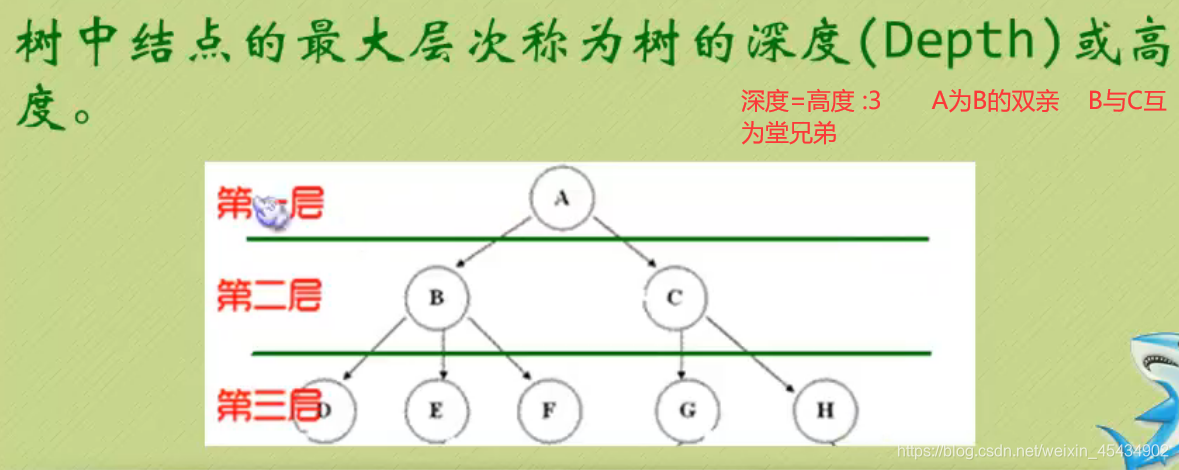
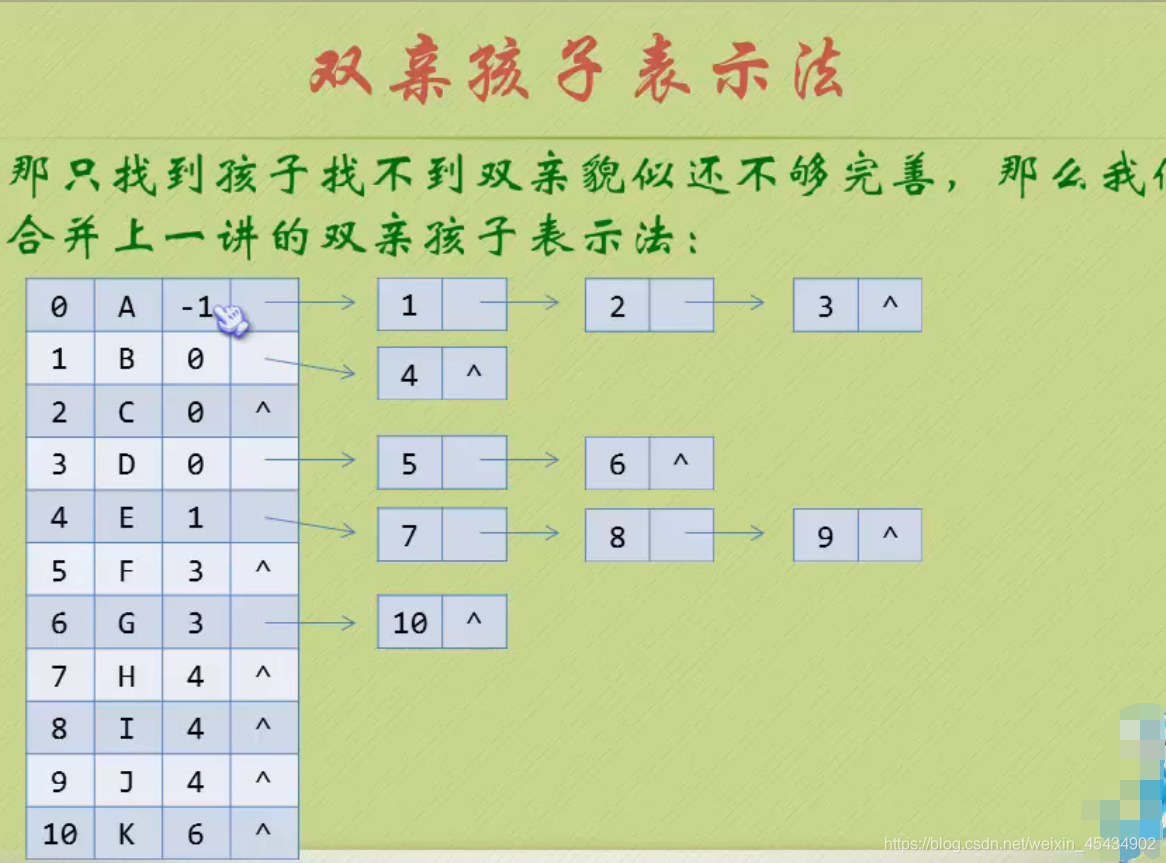
12 二叉树

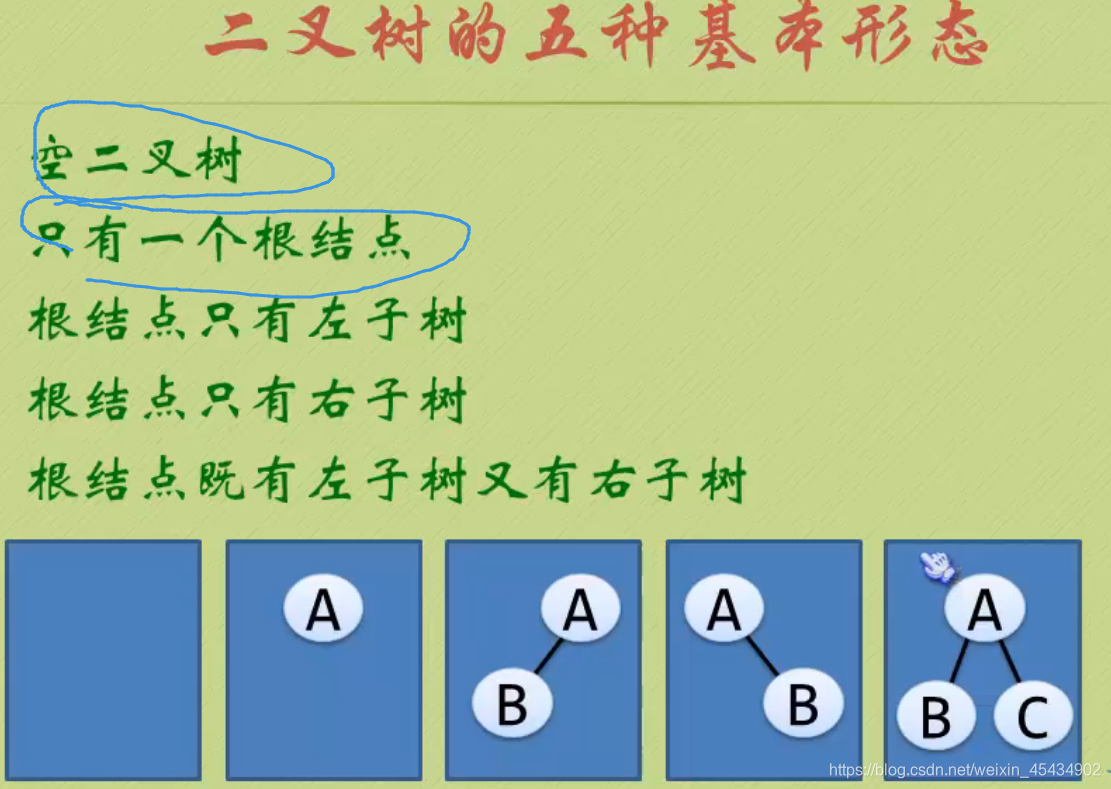
满二叉树: 叶子只能出现在最下一层,非叶子节点的度一定是 2

完全二叉树: 叶子节点只能出现在最下两层, 最下层叶子一定集中在左部连续位置,倒数第二层 叶子节点一定在右部连续位置

二叉树的性质:
1 第i层二叉树 有 2^(i-1) 个节点
2 深度为k的二叉树至多有 2^k – 1 个(总数)结点(k>=1)
3 叶子树(终端节点)为n0 度为2的节点树为 n0 => n2+1
4 连接数(线)= 总结点数–1 = n1+2*n2
5 具有n个结点的完全二叉树的深度为[log2n]取整+1

一般采用链式存储结构:

二叉树的遍历
序 相对于 根节点位置来说 俐:前序 根 左右

还有 中序 后序遍历…不一一列举了比较 相似
中序的话是从根节点开始
前后序的话是从叶子节点开始

二叉树的创建与遍历:
创建的话一般 都用前序创建




如果是后序遍历 把visit(T->data,level)放到 两个Pre后面

线索二叉树:
中序遍历 可以

*P: 根节点 T: 头指针

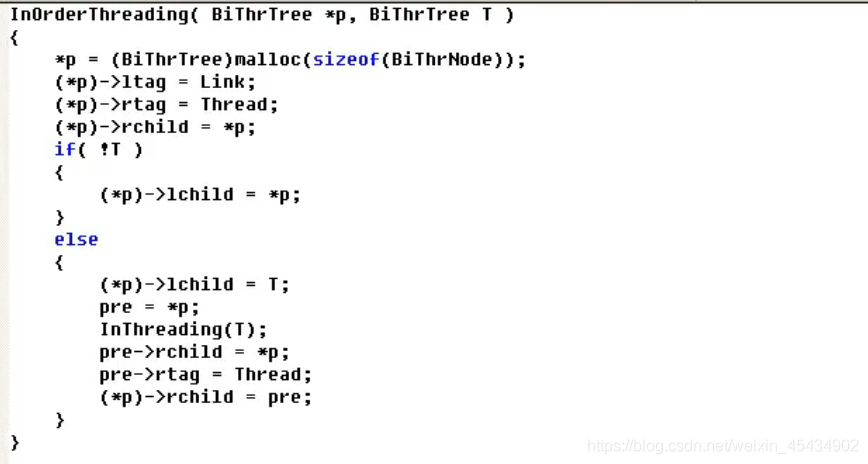
树 森林 及 二叉树 的相互转换

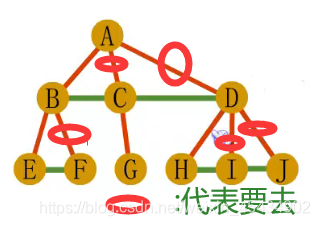
13 赫夫曼树(最小二叉树)

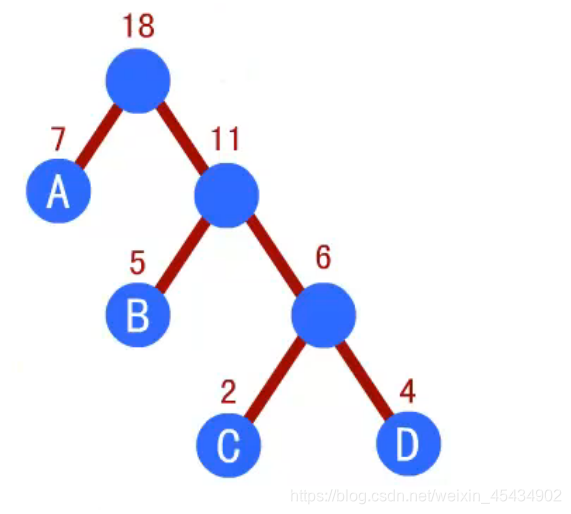
赫夫曼编码:

左 0 右1

*C++ 代码实现:*自己去搜把

14 图

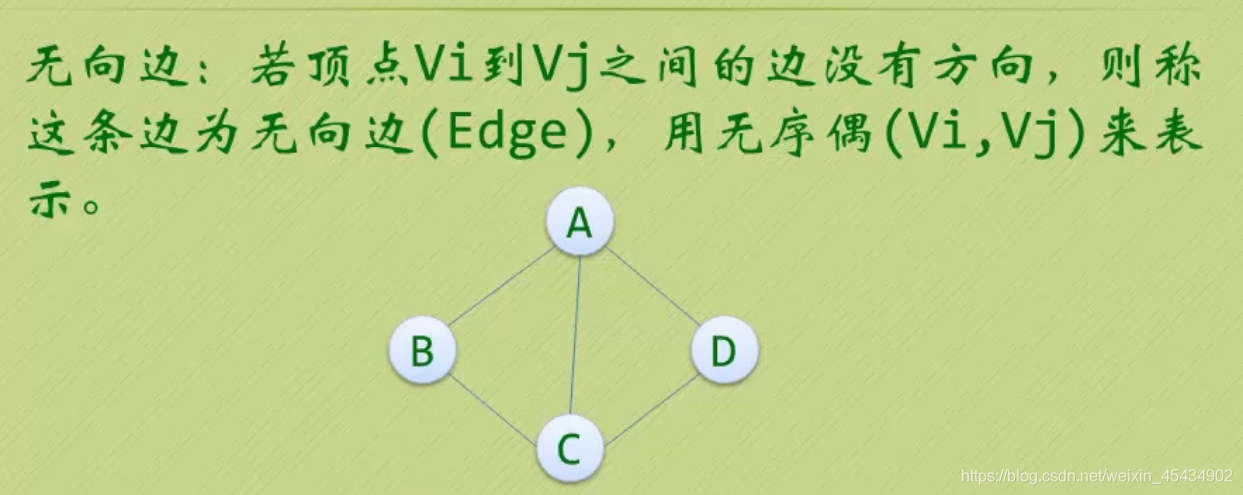
简单图: 没有环和平行边








存储结构:




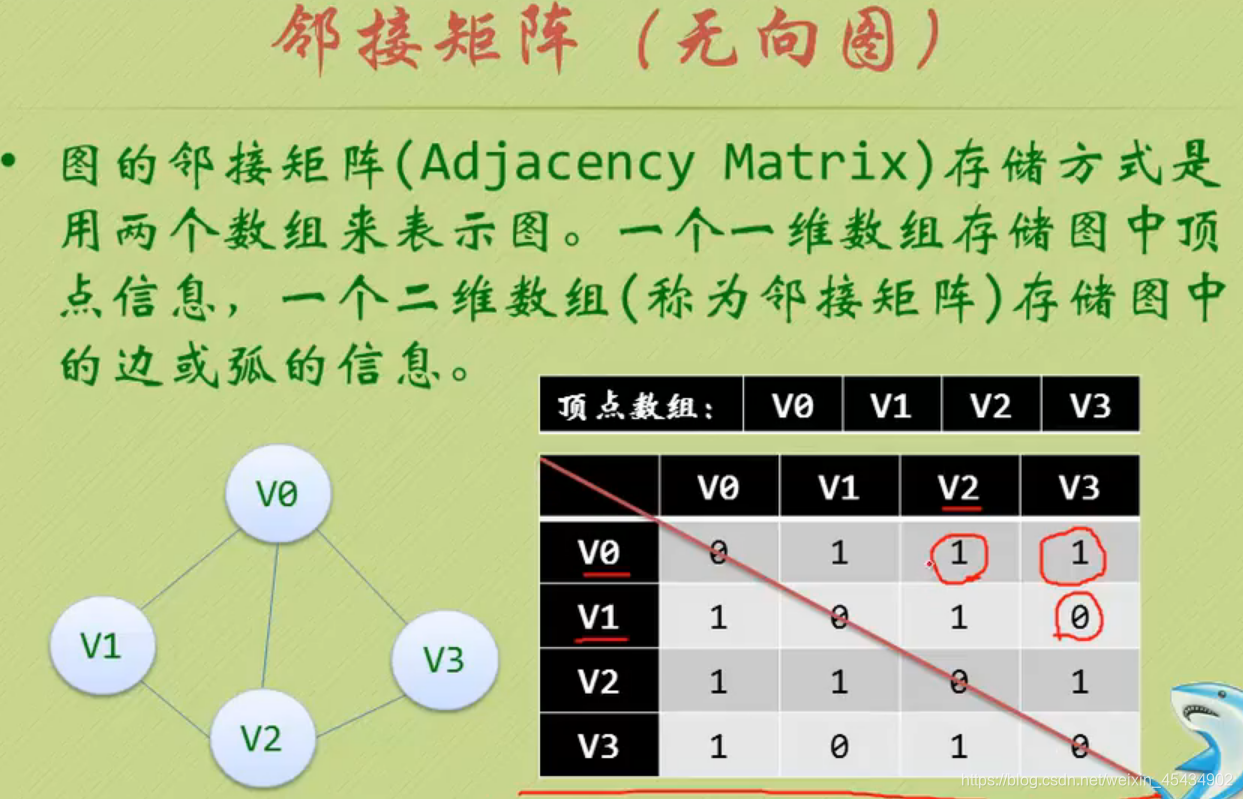
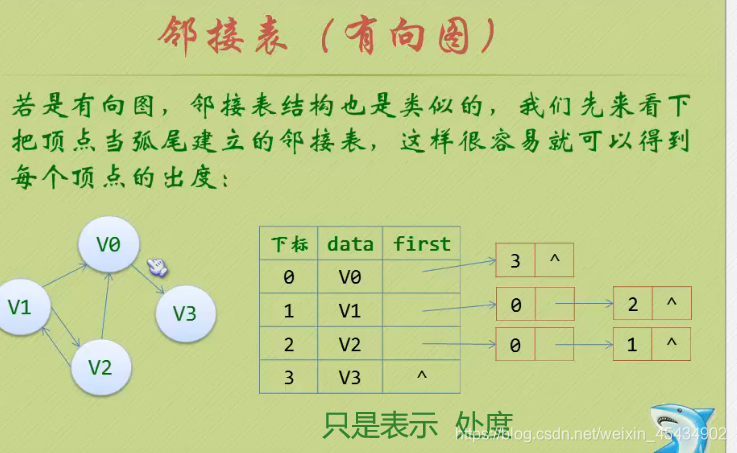
十字链表: 边表存的是一个边


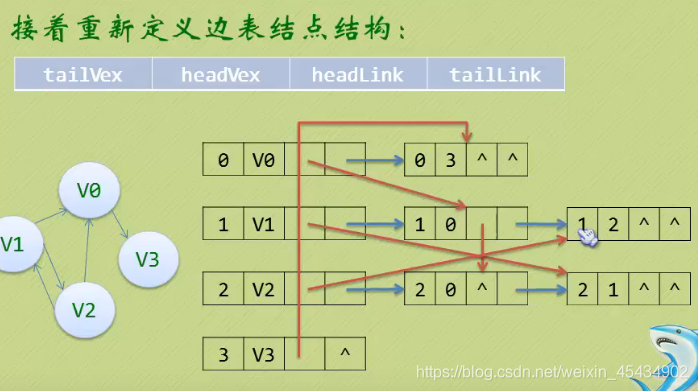
蓝表示 出度 || 红表示 入度
邻接多重表:


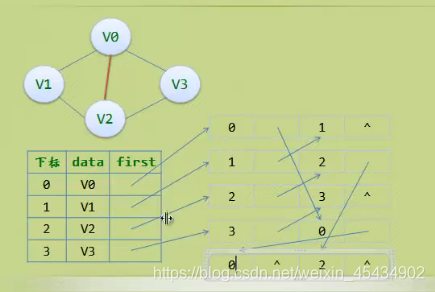
边集书组:

图的遍历:
1 深度优先遍历(搜索):
用递归哈

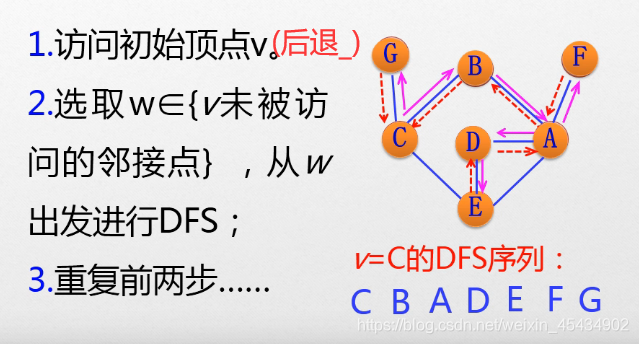
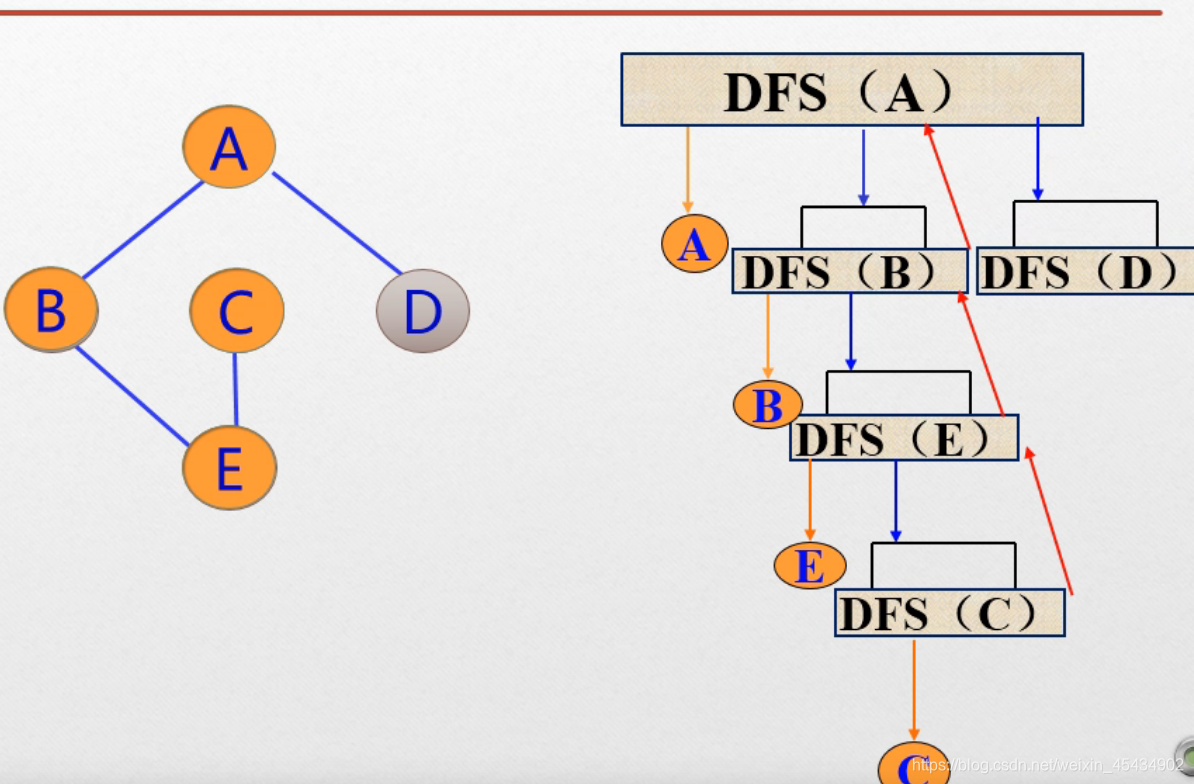
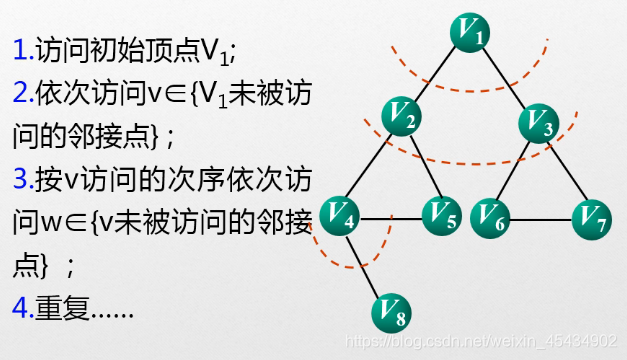
广度优先遍历(搜索):
也叫层序遍历, 用队列实现
队列一种“先进先出”的存储结构，即“一端入，一属端出”，队首(front)出队，队尾(rear)入队，若front指向队首，则rear指向队尾最后一个有效元素的 下一个 元素；若rear指向队尾，则front指向队首第一个有效元素的下一个元素。

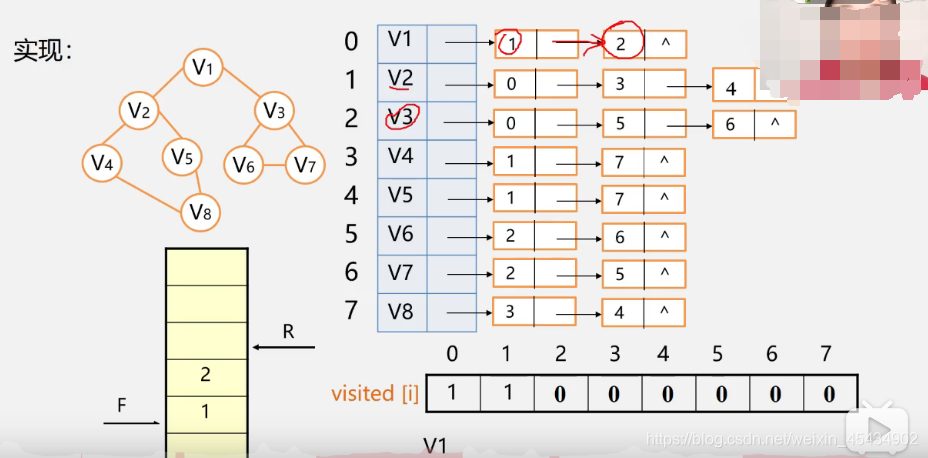
讯享网#include <stdio.h> #include <malloc.h> #define MAX 31  int visited[MAX]; typedef struct ArcNode { 
    int adjvex; //该弧指向的顶点的位置 struct ArcNode *nextarc; //指向下一条弧的指针 }ArcNode; typedef struct VNode { 
    char data; //顶点信息 struct ArcNode *firstarc; //指向第一条依附该顶点的弧的指针 }VNode, AdjList[MAX]; typedef struct { 
    AdjList adjlist; int vexnum, arcnum; //图的当前顶点数和弧数 }ALGraph; void CreateDG(ALGraph *G); //创建邻接表 void DispAdj(ALGraph *G); //输出邻接表 void DFS(ALGraph *G, int v); //深度优先遍历 void BFS(ALGraph *G, int v); //广度优先遍历 void CreateDG(ALGraph *G) { 
    int i, k, j, v1, v2; ArcNode *p; printf("输入图的顶点数和弧数:" ); scanf("%d,%d", &G->vexnum, &G->arcnum); printf("\n"); for(i = 1; i <= G->vexnum; i++) { 
    printf("输入第%d个顶点信息:", i); scanf("%s", &G->adjlist[i].data); } printf("\n"); for(i = 1; i <= G->vexnum; ++i) G->adjlist[i].firstarc = NULL; for(k = 1; k <= G->arcnum; ++k) { 
    printf("输入第%d条弧的弧尾和弧头:", k); scanf("%d,%d", &v1, &v2); i = v1; j = v2; p = (ArcNode *)malloc(sizeof(ArcNode)); p->adjvex = j; p->nextarc = G->adjlist[i].firstarc; G->adjlist[i].firstarc = p; } printf("\n"); } void DispAdj(ALGraph *G) { 
    int i; ArcNode *q; for(i = 1; i <= G->vexnum; ++i) { 
    q = G->adjlist[i].firstarc; printf("%d", i); while(q != NULL) { 
    printf("->%d", q->adjvex); q = q->nextarc; } printf("\n"); } } void DFS(ALGraph *G, int v) { 
    ArcNode *p; visited[v] = 1; printf("%3d", v); for(p = G->adjlist[v].firstarc; p != NULL; ) { 
    if(!visited[p->adjvex]) DFS(G, p->adjvex); p = p->nextarc; } } void BFS(ALGraph *G, int v) { 
    ArcNode *p; int queue[MAX], w, i; int front = 0, rear = 0; for(i = 0; i < MAX; i++) visited[i] = 0; printf("%3d", v); visited[v] = 1; rear = (rear + 1) % MAX; queue[rear] = v; while(front != rear) { 
    front = (front + 1) % MAX; w = queue[front]; p = G->adjlist[w].firstarc; while(p != NULL) { 
    if(visited[p->adjvex] == 0) { 
    printf("%3d",p->adjvex); visited[p->adjvex] = 1; rear = (rear+1) % MAX; queue[rear] = p->adjvex; } p = p->nextarc; } } printf("%\n"); } int main() { 
    //int i, j, k;  ALGraph *G; printf("\n"); G=(ALGraph *)malloc(sizeof(ALGraph)); CreateDG(G); printf("图的邻接表为:\n"); DispAdj(G); printf("\n"); printf("从顶点1开始的深度优先搜索:\n"); DFS(G, 1); printf("\n"); printf("从顶点1开始的广度优先搜索:\n"); BFS(G, 1); printf("\n"); return 0; } 

最小生成树(普鲁姆算法):

最小生成树(克鲁斯卡尔算法):

最短路径(Dijkstra算法)
把 顶点 放到 S中
o(n^2)

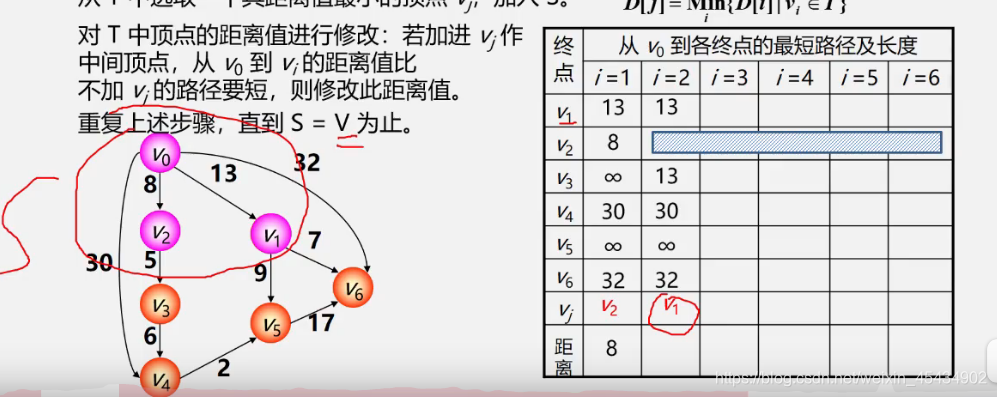
最短路径(弗洛伊德算法)
o(n*3)

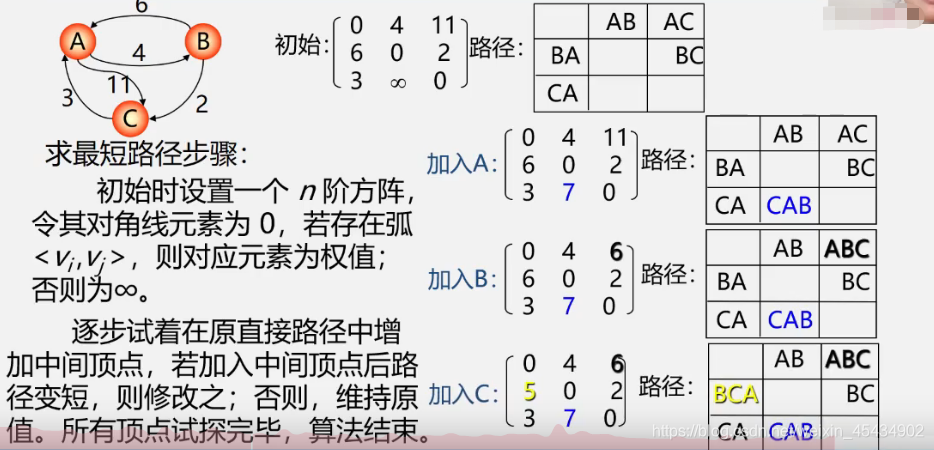
拓扑排序

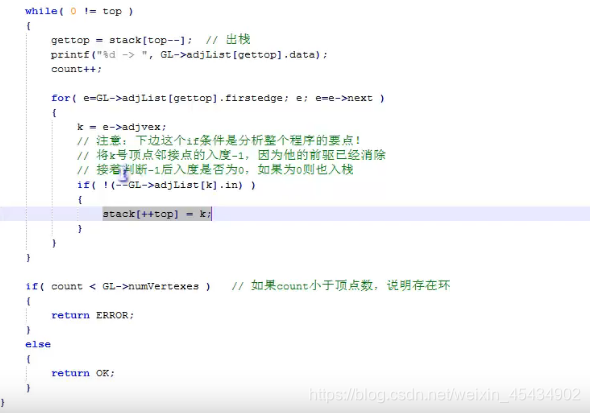
关键路径

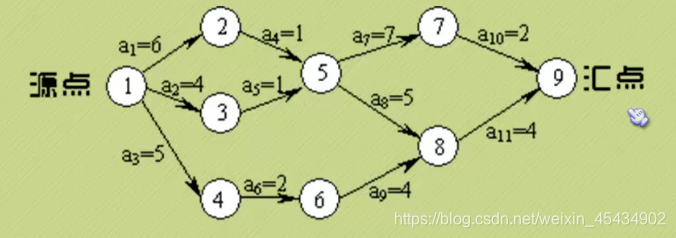
下面来看关键路径的算法代码。

15查找

顺序查找:

插值查找

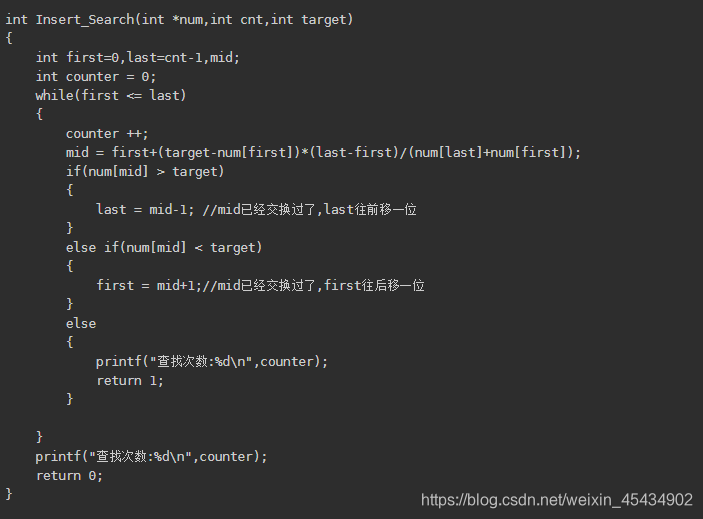
斐波那切数列

斐波那契查找的核心是： 1）当key=a[mid]时，查找成功；
2）当key<a[mid]时，新的查找范围是第low个到第mid-1个，此时范围个数为F[k-1] -
1个，即数组左边的长度，所以要在[low, F[k - 1] - 1]范围内查找；
3）当key>a[mid]时，新的查找范围是第mid+1个到第high个，此时范围个数为F[k-2] -
1个，即数组右边的长度，所以要在[F[k - 2] - 1]范围内查找。

先行索引查找
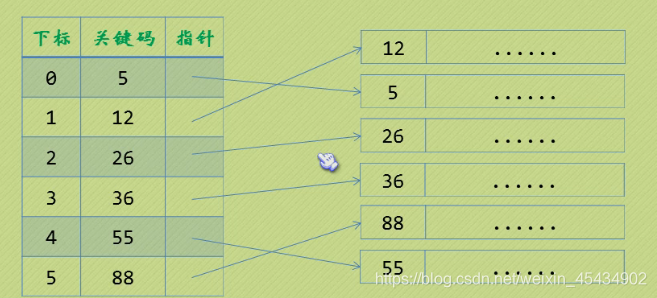
1稠密索引:

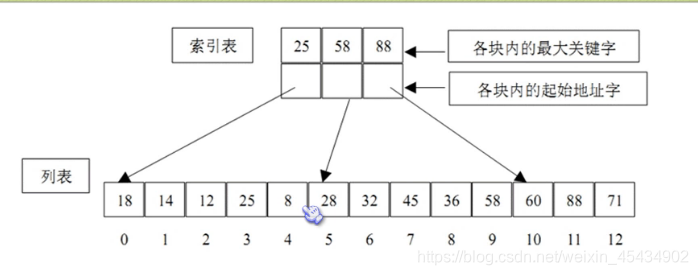
2 分块索引:

3 倒排索引:

16二叉排序树

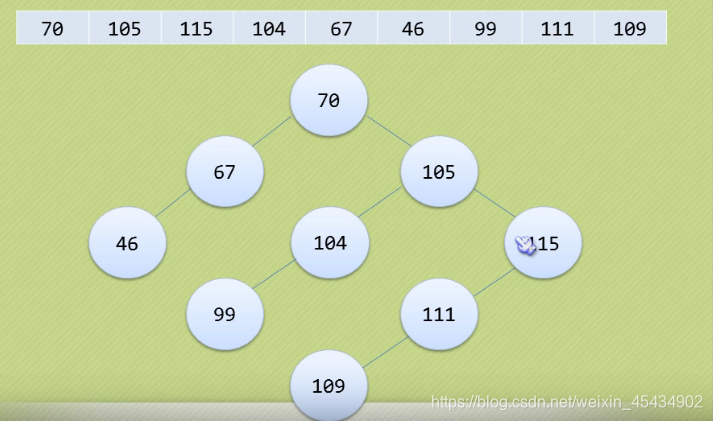
查找

插入

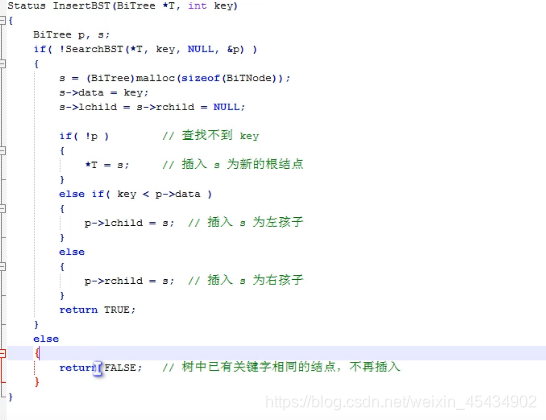
删除

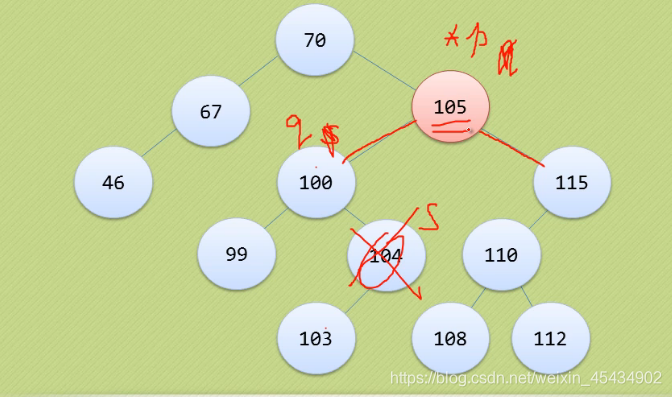
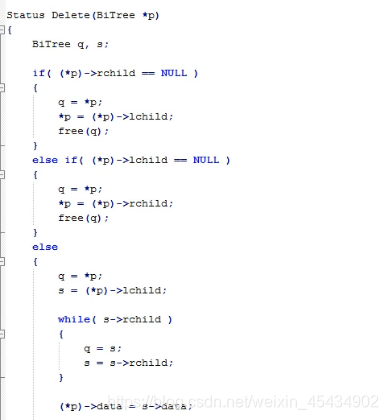
17平衡二叉树

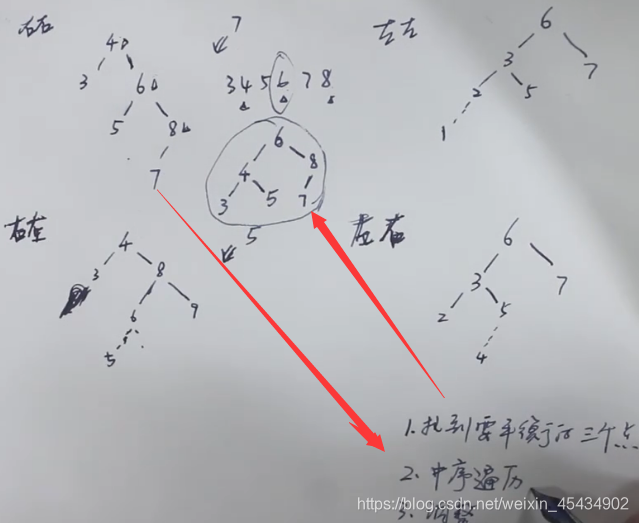
让其左平衡，进行右旋转，让其右平衡进行左旋转。T代表要旋转的树节点，L = T->lchild，Lr = L-rchild;R =
T->rchild,Rl = R->lchild; 但是要注意下面情况： 某个树节点T插入结点后，如果其左不平衡bf >
0，我们通过旋转让其左平衡。此时，其 L 左孩子的 bf 会影响如何旋转，如果L->bf = 1 同 T
方向一致，这是最简单的情况，只需将T进行右旋转。右平衡也是一样的道理。如果L->bf 和 T的方向不一致，那么就要先通过左旋转
让T->lchild和 T的方向一致，T在进行右旋转。 结合代码很好看明白

#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> typedef struct BiTNode { 
    int data; int bf; struct BiTNode* lchild, *rchild; }BiTNode, *BiTree; typedef enum{ 
   false,true}bool; //左旋转 void L_Rotate(BiTree *T) { 
    BiTree R = (*T)->rchild; (*T)->rchild = R->lchild; R->lchild = *T; *T = R; return; } //右旋转 void R_Rotate(BiTree *T) { 
    BiTree L = (*T)->lchild; (*T)->lchild = L->rchild; L->rchild = *T; *T = L; return; } #define LH +1 #define EH 0 #define RH -1 //T 的左边高，不平衡，使其平衡，右旋转，右旋转前先检查L->bf， //如果为RH，L要先进行左旋转，使T->lchild->bf和T->bf一致 void LeftBalance(BiTree* T) { 
    BiTree L,Lr; L = (*T)->lchild; Lr = L->rchild; switch (L->bf) { 
    case LH: L->bf = (*T)->bf = EH; R_Rotate(T); break; case RH: switch (Lr->bf) { 
    case LH: L->bf = EH; (*T)->bf = RH; break; case EH: L->bf = (*T)->bf = EH; break; case RH: L->bf = LH; (*T)->bf = EH; break; } Lr->bf = EH; L_Rotate(&L); R_Rotate(T); break; } } //T 的右边高，不平衡，使其平衡，左旋转，左旋转前先检查R->bf, //如果为LH，R要先进行右旋转，使T->rchild->bf和T->bf一致 void RightBalance(BiTree* T) { 
    BiTree R,Rl; R = (*T)->rchild; Rl = R->lchild; switch(R->bf) { 
    case RH: R->bf = (*T)->bf = EH; L_Rotate(T); break; case LH: switch(R->bf) { 
    case LH: R->bf = RH; (*T)->bf = EH; break; case EH: R->bf = (*T)->bf = EH; break; case RH: R->bf = EH; (*T)->bf = LH; break; } Rl->bf = EH; R_Rotate(&R); L_Rotate(T); break; } } //往平衡二叉树上插入结点 bool InsertAVL(BiTree* T,int data,bool *taller) { 
    if(*T == NULL) //找到插入位置 { 
    *T = (BiTree)malloc(sizeof(BiTNode)); (*T)->bf = EH; (*T)->rchild = (*T)->lchild = NULL; (*T)->data = data; *taller = true; } else { 
    if(data == (*T)->data) //树中有相同的结点数据直接返回 { 
    *taller = false; return false; } if(data < (*T)->data) //往左子树搜索进行插入 { 
    if(!InsertAVL(&(*T)->lchild,data,taller)) //树中有相同的结点 { 
    *taller = false; return false; } if (*taller) { 
    switch ((*T)->bf) //T插入结点后，检测平衡因子，根据情况，做相应的修改和旋转 { 
    case LH: LeftBalance(T); //插入后左边不平衡了，让其左平衡 *taller = false; break; case EH: (*T)->bf = LH; *taller = true; break; case RH: (*T)->bf = EH; *taller = false; break; } } } else //往右子树搜索进行插入 { 
    if(!Insert(&(*T)->rchild),data,taller) //树中有相同的结点 { 
    *taller = false; return false; } if (*taller) //插入到右子树中且长高了 { 
    switch ((*T)->bf) //T插入结点后，检测平衡因子，根据情况，做相应的修改和旋转 { 
    case LH: (*T)->bf = EH; *taller = false; break; case EH: (*T)->bf = RH; *taller = true; break; case RH: R_Balance(T); //插入后右边不平衡了，让其右平衡 *taller = false; break; } } } } return true; } 

18多路查找树

---

多路查找树(muitl-way search tree) 每个节点的孩子可以树可以多余两个； 每个节点可以存储多个元素；

---

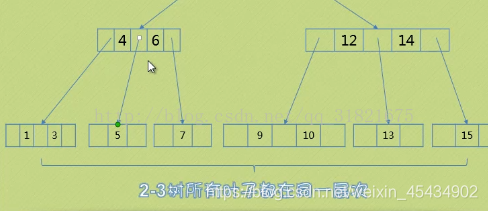
讯享网 1、2-3树 每个节点都具有2个孩子（称之为2节点）或者3个孩子（称之为3节点）。 一个2节点包含一个元素和两个孩子（或没有孩子）。 一个3节点包含两个元素和三个孩子（或没有孩子）。 

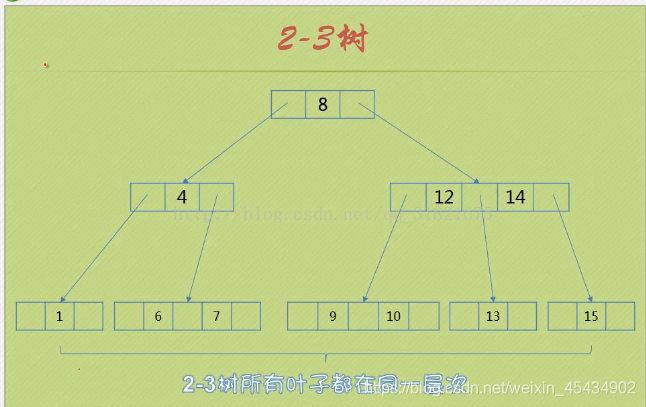
1.1. 2-3树的插入实现

 1.对于空树 插入一个节点直接插入就好。 2.插入节点到一个2节点的叶子上。 比如插入3 

3.将一个节点插入到原来上3节点的叶子上

讯享网 3.1要在3节点上插入，此时3节点的上面是2节点 则将 上面的2节点变成3节点 比如插入5 

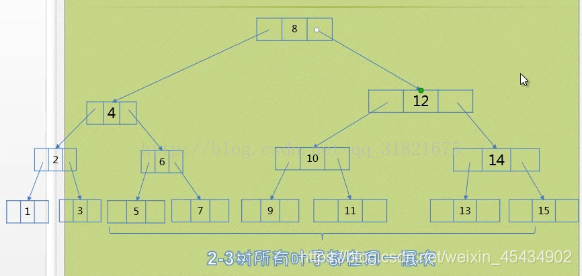
3.2 要在3节点上插入，此时3节点上面是3 节点 则将上面首次出现为2节点的节点变成3节点。比如插入11

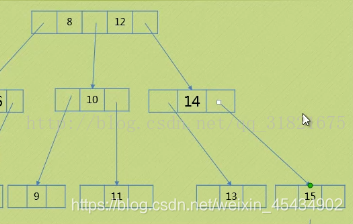
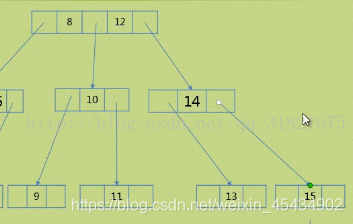
 以前我们普通二叉树 插入时都是在叶子节点后添加，这样会导致二叉树的高度不断增加。查找困难。 此时 我们用2-3树时重复分利用特性。 往上寻找有用空间 进行有效的利用 3.3 要在3节点插入数据时 ，该3节点往上遍历都是3节点，这时要扩展高度了。 

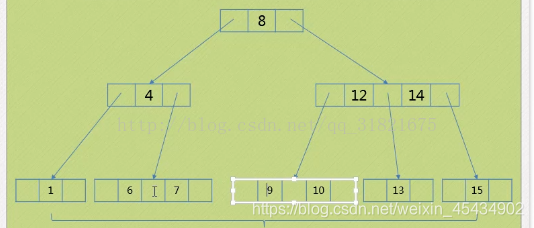
2-3树的删除实现。

讯享网 1.要删除的数位于3节点地址上。 3节点 ->2节点就好 比如删除6 

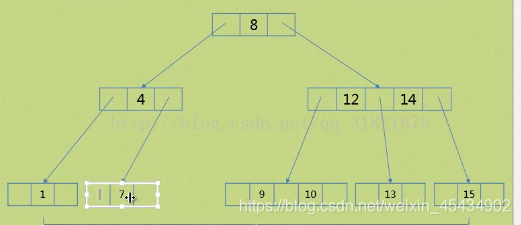
2.要删除的数位于2叶子节点上。

 1.此叶子节点上一级是2节点，但是他有一个3节点的有孩子。 

2.此叶子节点上一级是2节点，但是他有一个2节点的有孩子。

3.此叶子节点双亲是一个3节点。

4.删除的是一个满二叉树叶子节点

讯享网 5. 要删除的元素位于非叶子节点的分支上。 当是2节点时 则按照中序遍历 找此节点前面或者后面的数顶底 

当是3 节点的时候 将3节点的左孩子提升上去

2-3-4理论上跟2-3树是一样的

19散列表

什么是哈希表？

哈希表（Hash table，也叫散列表），是根据关键码值(Key
value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。
记录的存储位置=f(关键字)
这里的对应关系f称为散列函数，又称为哈希（Hash函数），采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表或哈希表（Hash
table）。 哈希表hashtable(key，value)
就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里。（或者：把任意长度的输入（又叫做预映射，
pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。）
而当使用哈希表进行查询的时候，就是再次使用哈希函数将key转换为对应的数组下标，并定位到该空间获取value，如此一来，就可以充分利用到数组的定位性能进行数据定位。
数组的特点是：寻址容易，插入和删除困难； 而链表的特点是：寻址困难，插入和删除容易。
那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表，哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法——拉链法，我们可以理解为“链表的数组”，如图：

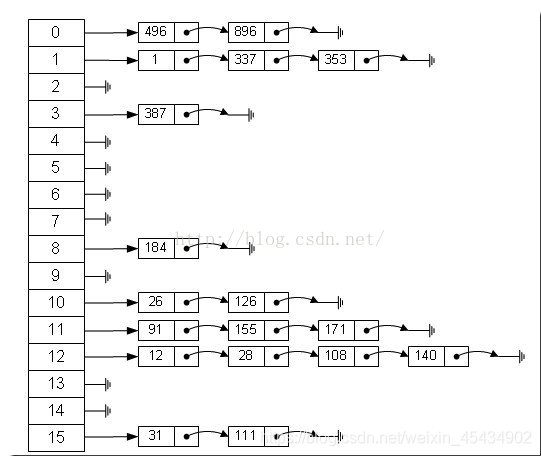
Hash的应用
1、Hash主要用于信息安全领域中加密算法，它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说，Hash就是找到一种数据内容和数据存放地址之间的映射关系。
2、查找：哈希表，又称为散列，是一种更加快捷的查找技术。我们之前的查找，都是这样一种思路：集合中拿出来一个元素，看看是否与我们要找的相等，如果不等，缩小范围，继续查找。而哈希表是完全另外一种思路：当我知道key值以后，我就可以直接计算出这个元素在集合中的位置，根本不需要一次又一次的查找！
举一个例子，假如我的数组A中，第i个元素里面装的key就是i，那么数字3肯定是在第3个位置，数字10肯定是在第10个位置。哈希表就是利用利用这种基本的思想，建立一个从key到位置的函数，然后进行直接计算查找。
3、Hash表在海量数据处理中有着广泛应用。

Hash Table的查询速度非常的快，几乎是O(1)的时间复杂度。

hash就是找到一种数据内容和数据存放地址之间的映射关系。

散列法：元素特征转变为数组下标的方法。

我想大家都在想一个很严重的问题：“如果两个字符串在哈希表中对应的位置相同怎么办？”,毕竟一个数组容量是有限的，这种可能性很大。解决该问题的方法很多，我首先想到的就是用“链表”。我遇到的很多算法都可以转化成链表来解决，只要在哈希表的每个入口挂一个链表，保存所有对应的字符串就OK了。

散列表的查找步骤
当存储记录时，通过散列函数计算出记录的散列地址
当查找记录时，我们通过同样的是散列函数计算记录的散列地址，并按此散列地址访问该记录

关键字——散列函数（哈希函数）——散列地址

优点：一对一的查找效率很高；

缺点：一个关键字可能对应多个散列地址；需要查找一个范围时，效果不好。

散列冲突：不同的关键字经过散列函数的计算得到了相同的散列地址。

好的散列函数=计算简单+分布均匀（计算得到的散列地址分布均匀）

哈希表是种数据结构，它可以提供快速的插入操作和查找操作。

优缺点

优点：不论哈希表中有多少数据，查找、插入、删除（有时包括删除）只需要接近常量的时间即0(1）的时间级。实际上，这只需要几条机器指令。

哈希表运算得非常快，在计算机程序中，如果需要在一秒种内查找上千条记录通常使用哈希表（例如拼写检查器)哈希表的速度明显比树快，树的操作通常需要O(N)的时间级。哈希表不仅速度快，编程实现也相对容易。

如果不需要有序遍历数据，并且可以****数据量的大小。那么哈希表在速度和易用性方面是无与伦比的。

缺点：它是基于数组的，数组创建后难于扩展，某些哈希表被基本填满时，性能下降得非常严重，所以程序员必须要清楚表中将要存储多少数据（或者准备好定期地把数据转移到更大的哈希表中，这是个费时的过程）。

元素特征转变为数组下标的方法就是散列法。散列法当然不止一种，下面列出三种比较常用的：

1，除法散列法
最直观的一种，上图使用的就是这种散列法，公式：
index = value % 16
学过汇编的都知道，求模数其实是通过一个除法运算得到的，所以叫“除法散列法”。

2，平方散列法
求index是非常频繁的操作，而乘法的运算要比除法来得省时（对现在的CPU来说，估计我们感觉不出来），所以我们考虑把除法换成乘法和一个位移操作。公式：
index = (value * value) >> 28 （右移，除以2^28。记法：左移变大，是乘。右移变小，是除。）
如果数值分配比较均匀的话这种方法能得到不错的结果，但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题，value如果很大，value * value不会溢出吗？答案是会的，但我们这个乘法不关心溢出，因为我们根本不是为了获取相乘结果，而是为了获取index。

3，斐波那契（Fibonacci）散列法

平方散列法的缺点是显而易见的，所以我们能不能找出一个理想的乘数，而不是拿value本身当作乘数呢？答案是肯定的。

1，对于16位整数而言，这个乘数是40503
2，对于32位整数而言，这个乘数是
3，对于64位整数而言，这个乘数是

散列冲突的解决方案：

1.建立一个缓冲区，把凡是拼音重复的人放到缓冲区中。当我通过名字查找人时，发现找的不对，就在缓冲区里找。

2.进行再探测。就是在其他地方查找。探测的方法也可以有很多种。

（1）在找到查找位置的index的index-1，index+1位置查找，index-2，index+2查找，依次类推。这种方法称为线性再探测。

（2）在查找位置index周围随机的查找。称为随机在探测。

（3）再哈希。就是当冲突时，采用另外一种映射方式来查找。

这个程序中是通过取模来模拟查找到重复元素的过程。对待重复元素的方法就是再哈希：对当前key的位置+7。最后，可以通过全局变量来判断需要查找多少次。我这里通过依次查找26个英文字母的小写计算的出了总的查找次数。显然，当总的查找次数/查找的总元素数越接近1时，哈希表更接近于一一映射的函数，查找的效率更高。
问题实例（海量数据处理）
我们知道hash 表在海量数据处理中有着广泛的应用，下面，请看另一道百度面试题：
题目：海量日志数据，提取出某日访问百度次数最多的那个IP。
方案：IP的数目还是有限的，最多2^32个，所以可以考虑使用hash将ip直接存入内存，然后进行统计。

20排序

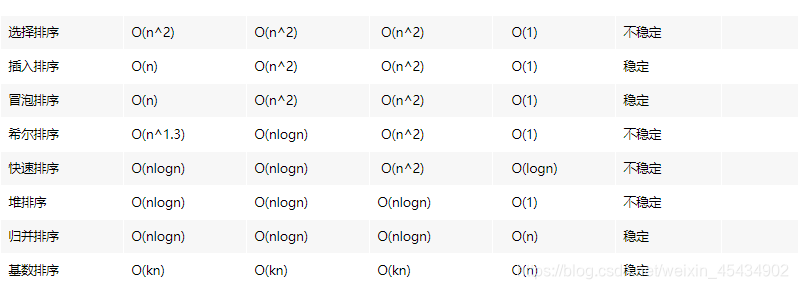
二、直接插入排序
方法：对于给定的一组记录，初始时假定第一个记录自成一个有序的序列，其余的记录为无序序列；接着从第二个记录开始，按照记录的大小依次将当前处理的记录插入到其之前的有序序列中，直至最后一个记录插入到有序序列为止。

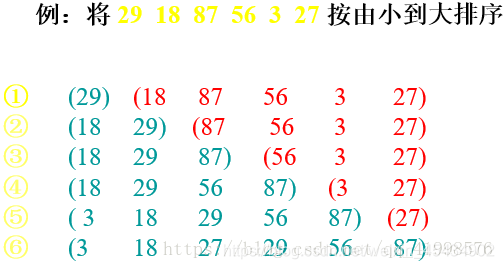
#include <stdio.h> void InsertSort(int array[], int len) { 
    int i, j, temp; for(i = 1; i < len; i++) { 
    temp = array[i]; for(j = i - 1; j >= 0; j--) { 
    if(temp < array[j]) { 
    array[j + 1] = array[j]; } else { 
    break; } } array[j + 1] = temp; } } int main() { 
    int i = 0; int a[] = { 
   8, 2, 5, 3, 6, 7, 1, 9, 0}; int length = sizeof(a) / sizeof(a[0]); InsertSort(a, length); for(i = 0; i < length; i++) { 
    printf("%d ", a[i]); } return 0; } 

三、希尔排序
希尔排序也称为“缩小增量排序”，基本原理是：首先将待排序的元素分为多个子序列，使得每个子序的元素个数相对较少，对各个子序分别进行直接插入排序，待整个待排序序列“基本有序后”，再对所有元素进行一次直接插入排序。

具体步骤如下：
(1)选择一个步长序列t1, t2, …, tk,满足ti > tj(i <ｊ)，tk = 1。
(2)按步长序列个数k，对待排序序列进行k趟排序。
(3)每趟排序，根据对应的步长ti，将待排序的序列分割成ti个子序列，分别对各个子序列进行直接插入排序。

讯享网#include <stdio.h> void ShellSort(int array[], int len) { 
    int i, j, temp, h; for(h = len / 2; h > 0; h = h / 2) { 
    for(i = h; i < len; i++) { 
    temp = array[i]; for(j = i - h; j >= 0; j -= h) { 
    if(temp < array[j]) { 
    array[j + h] = array[j]; } else { 
    break; } } array[j + h] = temp; } } } int main() { 
    int i = 0; int a[] = { 
   8, 2, 5, 3, 6, 7, 1, 9, 0}; int length = sizeof(a) / sizeof(a[0]); ShellSort(a, length); for(i = 0; i < length; i++) { 
    printf("%d ", a[i]); } return 0; } 

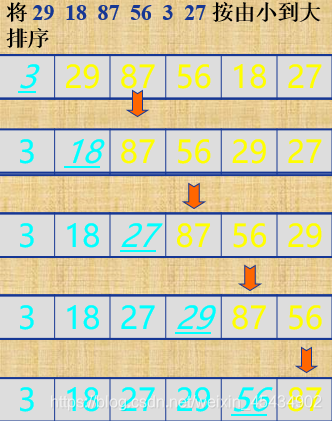
四、 冒泡排序

#include <stdio.h> void BubbleSort(int array[], int len) { 
    int i, j; int temp; for (i = 0; i < len -1; ++i) { 
    for (j = len - 1; j > i; --j) { 
    if (array[j] < array[j - 1]) { 
    temp = array[j]; array[j] = array[j - 1]; array[j - 1] = temp; } } } } int main() { 
    int i = 0; int a[] = { 
   29, 18, 87, 56, 3, 27}; int length = sizeof(a) / sizeof(a[0]); BubbleSort(a, length); for (i = 0; i < length; i++) { 
    printf("%d ", a[i]); } printf("\n"); return 0; } 

五、快速排序（高效）
采用“分而治之”的思想，把大的拆分为小的，小的在拆分为更小的。

原理：对于一组给定的记录，通过一趟排序后，将原序列分为两部分，其中前部分的所有记录均比后部分的所有记录小，然后再依次对前后两部分的记录进行快速排序，递归该过程，直到序列中的所有记录均为有序为止。

讯享网#include <stdio.h> int a[30], n; void QuickSort(int left, int right) { 
    int i, j, tmp, tmp1; i = left; j = right; if(left >= right) { 
    return; } while(i < j) { 
    while(a[j] >= a[left] && i < j) //left作为参考值 { 
    j--; } while(a[i] <= a[left] && i < j) { 
    i++; } if(i < j) { 
    tmp = a[i]; a[i] = a[j]; a[j] = tmp; } } tmp1 = a[i]; a[i] = a[left]; a[left] = tmp1; QuickSort(left, i - 1); QuickSort(i + 1, right); } int main() { 
    int i; printf("Please input n:\n"); scanf("%d", &n); printf("Please input number:\n"); for(i = 1; i <= n; i++) { 
    scanf("%d", &a[i]); } QuickSort(1, n); for(i = 1; i <= n; i++) { 
    printf("%d ", a[i]); } return 0; } 

六、简单选择排序
对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将记录与第一个记录的位置进行交换；接着对不包括第一个记录以外的其他记录进行第二轮排序，得到最小的记录并与第二个记录进行位置交换；重复该过程，直到进行比较的记录只有一个为止。

#include <stdio.h> void SelectSort(int *num, int n) { 
    int i, j; int tmp = 0, min = 0; for(i = 0; i < n - 1; i++) { 
    min = i; for(j = i + 1; j < n; j++) { 
    if(num[j] < num[min]) { 
    min = j; } } if(min != i) { 
    tmp = num[i]; num[i] = num[min]; num[min] = tmp; } } } int main() { 
    int i, len; int num[] = { 
   4, 8, 2, 4, 0, 9, 1, 3, 5}; len = sizeof(num) / sizeof(num[0]); SelectSort(num, len); for(i = 0; i < len; i++) { 
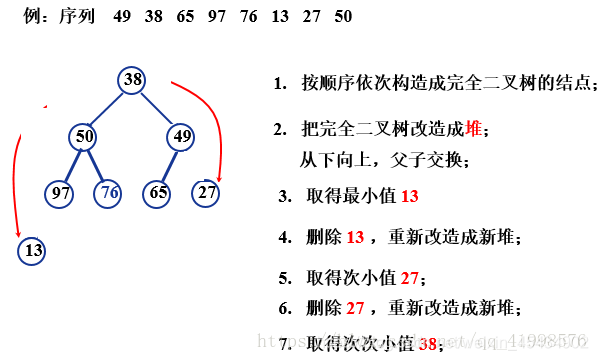
    printf("%d ", num[i]); } return 0; } 

七、堆排序
将序列构造成一棵完全二叉树 ；
把这棵普通的完全二叉树改造成堆，便可获取最小值 ；
输出最小值 ；
删除根结点，继续改造剩余树成堆，便可获取次小值 ；
输出次小值 ；
重复改造，输出次次小值、次次次小值，直至所有结点均输出，便得到一个排序 。

讯享网#include <stdio.h>//适用于数据量大的时候(构建浪费时间) void AdjustMinHeap(int *array, int pos, int len) { 
    int tmp, child; for(tmp = array[pos]; 2 * pos + 1 <= len; pos = child) { 
    child = 2 * pos + 1; if(child < len && array[child] > array[child + 1]) { 
    child++; } if(array[child] < tmp) { 
    array[pos] = array[child]; } else { 
    break; } } array[pos] = tmp; } void Swap(int *a, int *b) { 
    int temp; temp = *a; *a = *b; *b = temp; } void HeapSort(int *array, int len) { 
    int i; for(i = len/2 - 1; i >= 0; i--) { 
    AdjustMinHeap(array, i, len - 1); } for(i = len - 1; i >= 0; i--) { 
    Swap(&array[0], &array[i]); AdjustMinHeap(array, 0, i - 1); } } int main() { 
    int i; int array[] = { 
   0, 13, 14, 1, 18, 27}; int length = sizeof(array) / sizeof(array[0]); HeapSort(array, length); for(i = 0; i < length; i++) { 
    printf("%d ", array[i]); } return 0; } 

八、归并排序
利用递归与分治技术将数据序列划分为越来越小的半子表，再对半子表排序，最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列。
原理：对于给定的一组记录，首先将两个相邻的长度为1的子序列进行归并，得到n/2个长度为2或者1的有序子序列，在将其两两归并，反复执行此过程，直到得到一个有序的序列为止。

#include <stdio.h> #include <stdlib.h> void Merge(int array[], int start, int middle, int end) { 
    int i, j, k, n1, n2; n1 = middle - start + 1; n2 = end - middle; int *L = (int *)malloc(n1 * sizeof(int)); int *R = (int *)malloc(n2 * sizeof(int)); for (i = 0, k = start; i < n1; i++, k++) { 
    L[i] = array[k]; } for (i = 0, k = middle + 1; i < n2; i++, k++) { 
    R[i] = array[k]; } for (k = start, i = 0, j = 0; i < n1 && j < n2; k++) { 
    if (L[i] < R[j]) { 
    array[k] = L[i]; i++; } else { 
    array[k] = R[j]; j++; } } if (i < n1) { 
    for (j = i; j < n1; j++, k++) { 
    array[k] = L[j]; } } if (j < n2) { 
    for (i = j; i < n2; i++, k++) { 
    array[k] = R[i]; } } } void MergeSort(int array[], int start, int end) { 
    int middle; int i; if (start < end) { 
    middle = (start + end) / 2; MergeSort(array, start, middle); MergeSort(array, middle + 1, end); Merge(array, start, middle, end); } } int main() { 
    int i = 0; int a[] = { 
   49, 38, 65, 97, 76, 13, 27}; int length = sizeof(a) / sizeof(a[0]); MergeSort(a, 0, length -1); for (i = 0 ; i < length; i++) { 
    printf("%d ", a[i]); } printf("\n"); return 0; } 

觉得不错的 关注我点个赞 带你看更多技术和面试干货 么么哒