1、SMO高效优化算法
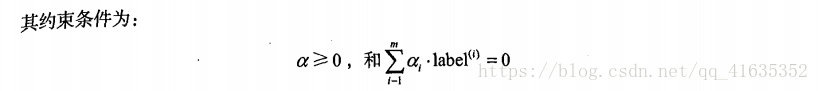
对这两个式子进行优化。下面我们开始讨论SMO算法,然后给出一个简化版本以便理解它的工作流程,最后才将会给出完整的算法,它比简化版的运行速度要快很多。
platt的SMO算法
SMO表示 序列最小优化,将大优化问题分解为多个小优化问题来求解。这些小优化问题往往很容易进行求解,并且对它们进行顺序求解的结果与将它们作为整体来求解的结果是完全一致的。在结果完全相同的同时,SMO算法的求解时间会短很多。
应用简化版SMO算法处理小规模数据集
我们先对算法进行简化处理,了解基本思路,在基于简单版实现完整版。Platt SMO算法中的外循环要确定优化的**alpha对,而简化版却会跳过这个部分,首先在数据集上遍历每一个alpha,然后在剩下的alpha集合中随机选择另一个alpha,从而构建alpha对。这里有一点相当重要,就是我们要同时该表两个alpha。之所以这样是因为约束条件:
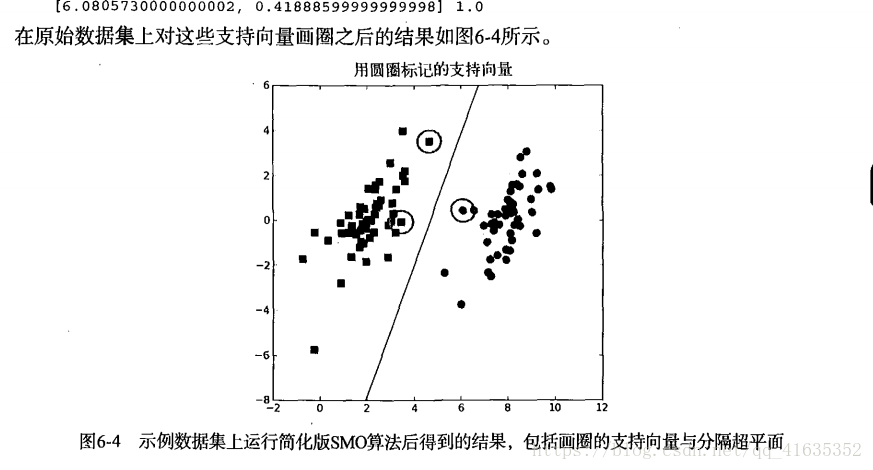
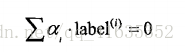 由于改变一个alpha值可能会导致约束条件失效,所以我们总是同时改变两个alpha。
由于改变一个alpha值可能会导致约束条件失效,所以我们总是同时改变两个alpha。
#得到每行的类标签和整个数据矩阵 def loadDataSet(fileName): dataMat = [] labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = line.strip().split('\t') #dataMat.append([float(lineArr[0]), float(lineArr[1])]) dataMat.append([float(lineArr[0]), float(lineArr[1])]) labelMat.append(float(lineArr[2])) return dataMat, labelMat #i:alpha的下标 m:所有alpha的数目,只要函数值不等于输入值i,函数就会随机选择 def selectJrand(i, m): j = i while(j == i): j = int(random.uniform(0, m)) return j #用于调整大于H或小于L的alpha值 def clipAlpha(aj, H, L): if aj > H: aj = H if L > aj: aj = L return aj讯享网
每个函数的功能都写在函数中了。上述工作完成之后,就可以使用SMO算法的第一个版本了,伪代码大致如下:
创建一个alpha向量并将其初始化为0向量

讯享网def smoSimple(dataMatIn, classLabels, C, toler, maxIter): ''' 输入参数:数据集, 类别标签, 常数C, 容错率, 取消最大循环的次数 ''' #将输入参数转化为numpy矩阵 dataMatrix = mat(dataMatIn) #标签为列向量,这样标签中的每行元素就和数据矩阵中的行一一对应了 labelMat = mat(classLabels).T b = 0 # m,n m,n = shape(dataMatrix) #构建一个alpha列矩阵 alphas = mat(zeros((m,1))) #用于存储在没有任何alpha改变的情况下遍历数据集的次数。当该变量到达输入值maxIter时,函数结束运行并退出 iter = 0 #开始循环 #只有在所有数据集遍历maxIter次数之后且不再发生任何alpha修改后,程序才会退出循环 while(iter < maxIter): #先设为0,用于记录alpha是否已经进行优化 alphaPairsChanged = 0 for i in range(m): #fXi能够倍计算出来,这就是我们预测的类别 fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b #基于实例的预测结果和真实结果对比计算误差Ei Ei = fXi - float(labelMat[i]) ''' 如果误差很大,那么可以对该数据实例所对应的alpha值进行优化 在if的判断中: 不管是正间隔还是负间隔都会被测试,同时还要检测alpha值不能等于0或C 因为后面alpha的值小于0或大于C时将被调整为0或C,所以一旦alpha为0或C, 那么它们就在边界上了,因而不能够再增大或减小,因此也就不值得对它们进行优化了 ''' if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler)and (alphas[i]>0)): #利用辅助函数随机选择第二个alpha值 j = selectJrand(i, m) #计算选择的第二个alpha的误差 fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b Ej = fXj - float(labelMat[j]) #为alphaIold,alphaJold分配新的内存,以便观察新旧值的变化 alphaIold = alphas[i].copy() alphaJold = alphas[j].copy() #计算L,H ,它们用于将alpha[j]的值调整到0和C之间 #如果L和H相等,就不做任何改变,直接执行continue语句,本循环结束直接运行下一次 if (labelMat[i] != labelMat[j]): L = max(0, alphas[j] - alphas[i]) H = min(C, C+alphas[j] - alphas[i]) else: L = max(0, alphas[j] + alphas[i] - C) H = min(C, alphas[j] + alphas[i]) if (L == H): print("L == H") continue #alpha[j]的最优修改量 eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T if (eta>=0): print("eta>0") continue #简化了SMO算法,并计算新的alpha[j] alphas[j] -= labelMat[j]*(Ei - Ej)/eta #辅助函数调整alpha[j]的值 alphas[j] = clipAlpha(alphas[j],H,L) #检查alpha[j]是否有轻微的改变 if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue #alpha[i]和alpha[j]同样进行改变,大小一样,方向相反。 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold-alphas[j]) #alpha优化之后,给这两个值设置一个常数项b b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T if (0<alphas[i]) and (C>alphas[i]): b = b1 elif(0<alphas[j]) and (C > alphas[j]): b = b2 else: b = (b1 + b2)/2.0 #执行到for的最后一行都没有执行continue语句,那么就成功的改变了一对alpha,增加计数值 alphaPairsChanged += 1 print("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)) #在for循环之外需要检查alpha的值是否进行了更新 if (alphaPairsChanged == 0): iter += 1 #如果alpha的值更新了则将iter的值设为0后继续运行 else: iter = 0 print ("iteration number: %d" % iter) return b,alphas
我们对上面的结果进行查看:

alpha中有太多的0了。我们只看非零的元素有一下三个

下面我们观察输入样本中的支持向量:即对应alpha大于0的,有三个


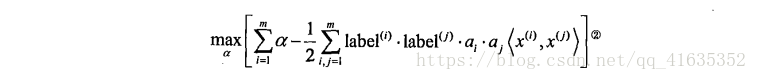
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/54340.html