目录

前言

一、求阶乘

1、第一种方法

2、第二种方法

3、第三种方法

4、第四种方法

 5、第五种方法

6、第六种方法

二、斐波那契数列

1、第一种方法

2、第二种方法

3、第三种方法

前言

        最近在python技能树重温以前学过的Python知识，把自己从知道点的大白又打回了小白了。知识果然知道的越多越觉得自己的不足。这个球的半径越大，空白也就越多。居安思危，日进尺步。分享几个我最近的学到的求阶乘、斐波那契的别样实现方法分享给大家。

一、求阶乘

0,1,2,3,4,5,6,7,8,9,10! 令人惊讶的是，6个星期的秒数居然也等于10!

不使用函数递归，实现一个阶乘计算函数(n<=170)：

1、第一种方法

代码：

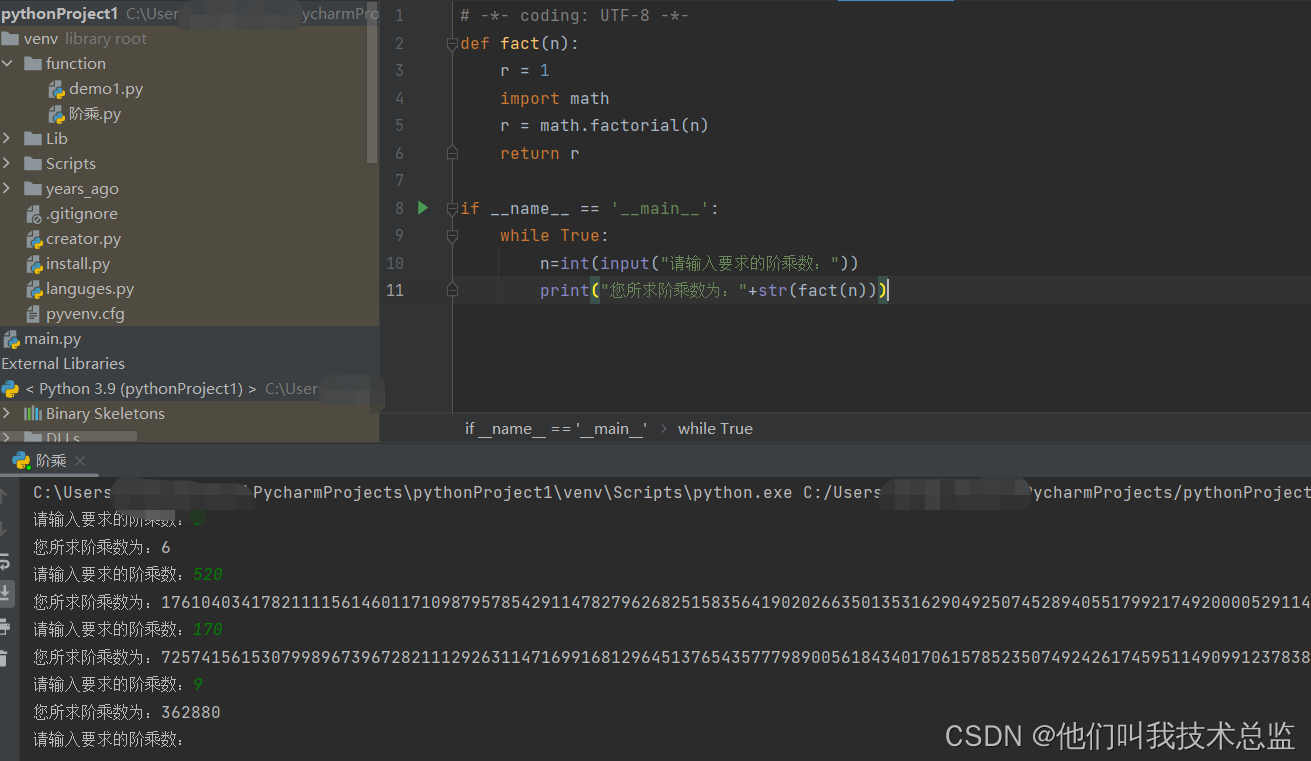
# -*- coding: UTF-8 -*- def fact(n): r = 1 import math r = math.factorial(n) return r if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

效果：

讯享网

解析：利用python中math的自带函数 factorial，我们查看函数源码可以发现，该函数正式用于求阶乘的。

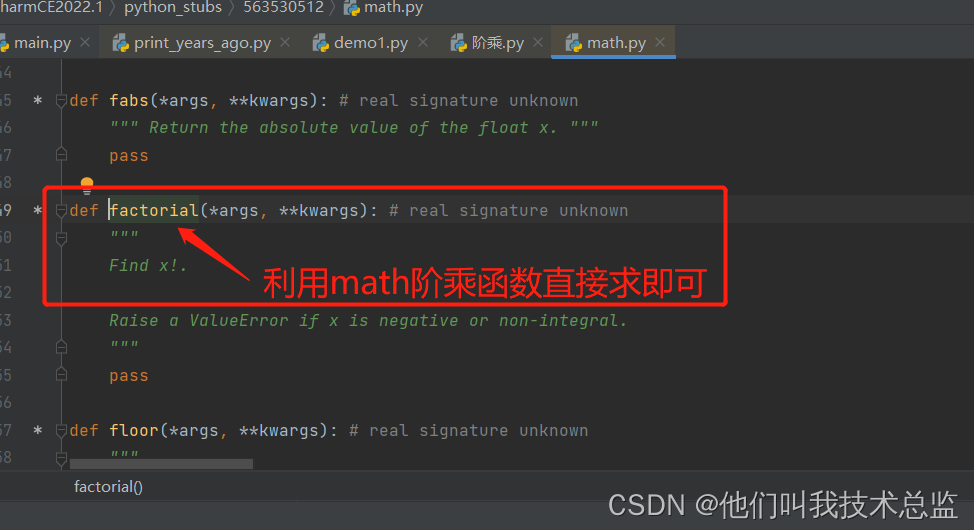
2、第二种方法

代码：

讯享网def fact(n): r = 1 for i in range(0, n): r *= (i + 1) return r if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

效果： 

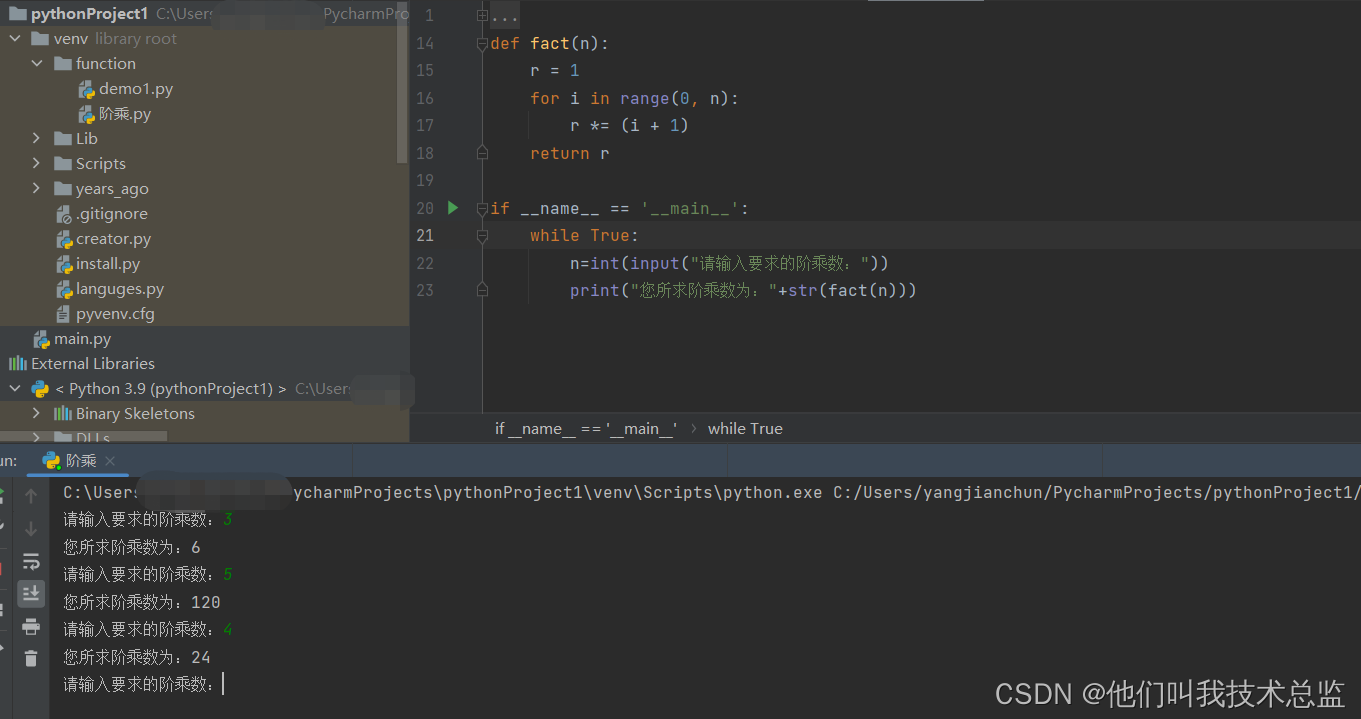
解析：

利用for循环来计算对应阶乘即 s=1*2*....*n-1*n妥妥的数学最初对阶乘的解释。

3、第三种方法

代码：

# # -*- coding: UTF-8 -*- # def fact(n): # r = 1 # import math # r = math.factorial(n) # return r # # if __name__ == '__main__': # while True: # n=int(input("请输入要求的阶乘数：")) # print("您所求阶乘数为："+str(fact(n))) # # -*- coding: UTF-8 -*- def fact(n): r = 1 # for i in range(0, n): # r *= (i + 1) while n > 0: r *= n n -= 1 return r if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

效果：

解析：此方法与方法二异曲同工之妙，只是s=n*n-1*...*2*1，哈哈哈，甚是有趣。

4、第四种方法

代码：

讯享网def inner_fact(n, m): if m == n: return n return m*inner_fact(n, m+1) def fact(n): return inner_fact(n,1) if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

效果：

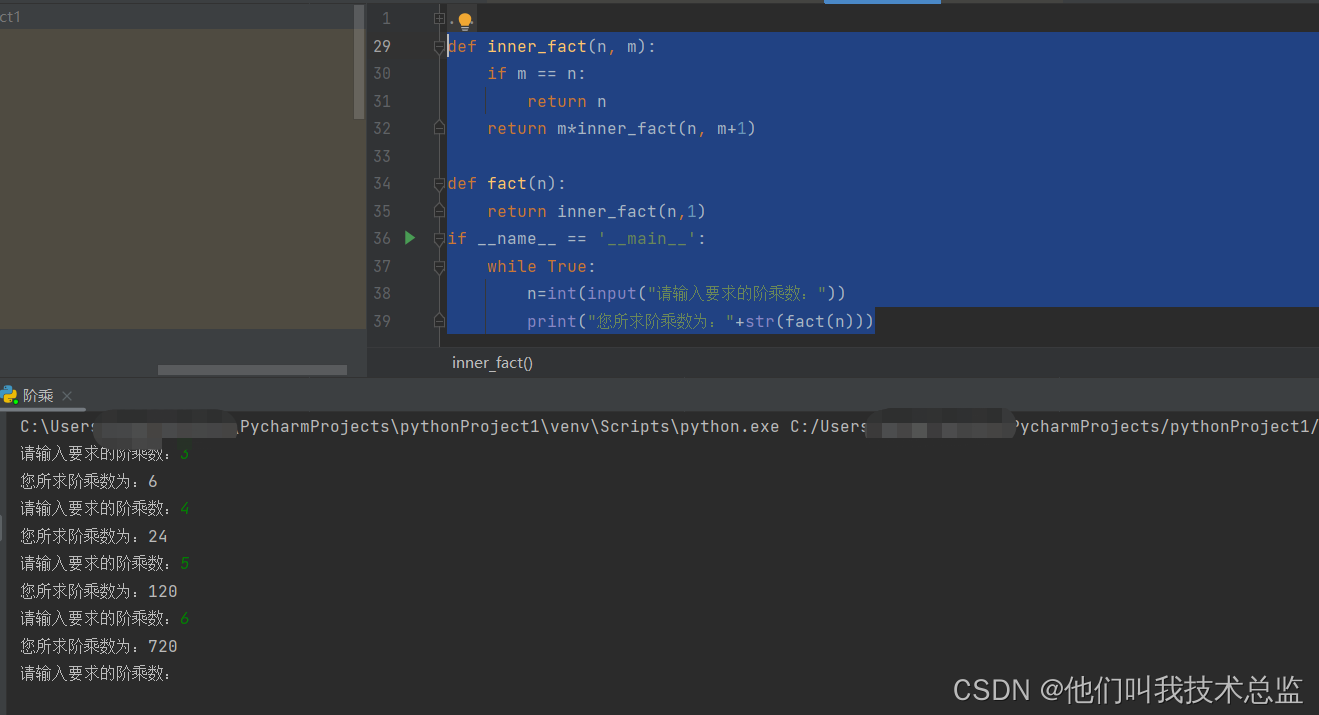
解析：

 此方法使用函数调用子函数来循环计算，思路与上面两种一致，但看起来稍显复杂。

 5、第五种方法

代码：

def inner_fact(n, r): if n == 1: return r return inner_fact(n-1, r*n) def fact(n): return inner_fact(n, 1) if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

效果：

 解析：此方法是第三种方法的变式，只不过是在函数中进行循环判断。

6、第六种方法

代码：

讯享网def fact(n): if n == 1: return 1 return n*fact(n-1) if __name__ == '__main__': while True: n=int(input("请输入要求的阶乘数：")) print("您所求阶乘数为："+str(fact(n)))

 效果：

解析：此方法运用函数的自递归来完成运算。 

二、斐波那契数列

        数学家莱昂纳多·斐那契（Leonardo Fibonacci）以兔子繁殖为例子引入了数列0、1、1、2、3、5、8、13、21、34...，称为斐波那契数列（Fibonacci sequence），又称“黄金分割数列”或者“兔子数列”。使用函数递归或非递归的方式都可以方便地计算斐波那契函数：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2）

1、第一种方法

代码：

def fibonacci(n): from math import pow, sqrt return int(1/sqrt(5)*(pow((1+sqrt(5))/2, n)-pow((1-sqrt(5))/2, n))) if __name__ == '__main__': while True: n=int(input("请输入要求的斐波那契数：")) print("您所求斐波那契数数列为："+str(fibonacci(n)))

效果：

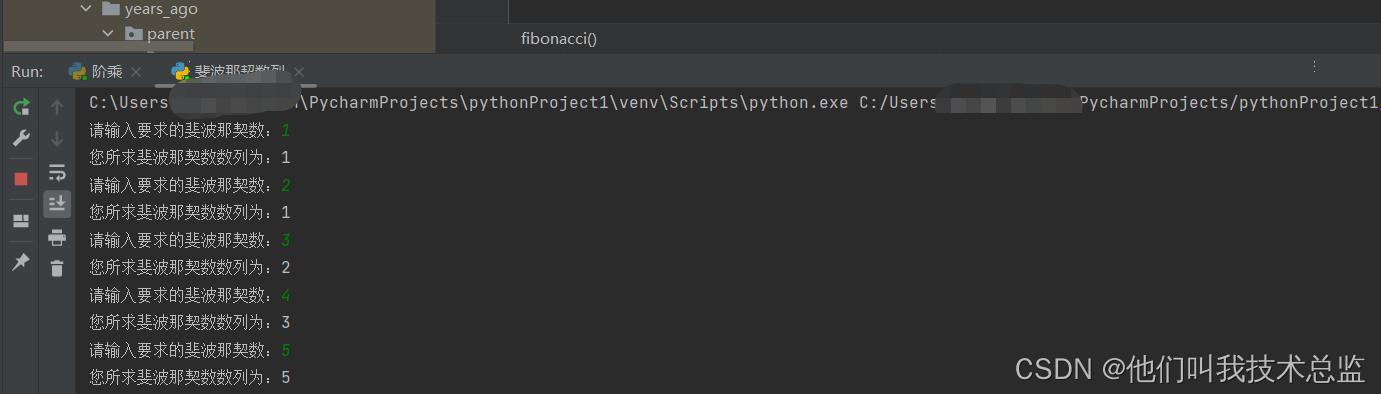
解析：使用平方根与幂运算然后取整算出对应斐波那契数

2、第二种方法

代码：

讯享网def fibonacci(n): if n == 1 or n == 2: return 1 return fibonacci(n-1) + fibonacci(n-2) if __name__ == '__main__': while True: n=int(input("请输入要求的斐波那契数：")) print("您所求斐波那契数数列为："+str(fibonacci(n)))

效果：

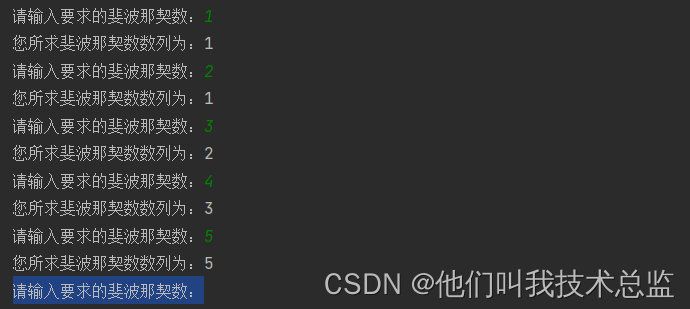
解析：通过循环调用然后再计算累计值。

3、第三种方法

代码：

def fibonacci_inner(n, m, r0, r1): if m == n: return r1 return fibonacci_inner(n, m+1, r1, r0+r1) def fibonacci(n): return fibonacci_inner(n, 2, 1, 1) if __name__ == '__main__': while True: n=int(input("请输入要求的斐波那契数：")) print("您所求斐波那契数数列为："+str(fibonacci(n)))

效果：

解析：此方法与上面一种差异不大，只是将每次计算值用r来保存起来