3D中的方位与角位移

科技前沿 • 2025-01-04 23:48 • 阅读 69

大家好，我是讯享网，很高兴认识大家。

摘要：本文讲述了3D中描述方位与角位移的方法：矩阵、欧拉角和四元数，以及它们优缺点和适用场景。给理解Gimbal Lock提供了一种新视角。

1. 简介

“方位”是指物体的朝向，是一个状态；“旋转”可以把物体从一个方位变到另一个方位，是一个动作；“角位移”是旋转的量。
方位和角位移的关系类似于“位置”和“位移”的关系。
物体的位置是不能用绝对坐标来描述的，我们必须将其放置在一个坐标系内，通过描述物体相对于参考点的位移来描述物体的位置。例如，位于（100，0，20）的点，表示的是跟原点（0，0，0）的位移是（100，0，20）的位置。
类似的，方位也是通过相对已知方位的角位移来描述的。

描述角位移有3种最常用的方法：矩阵、欧拉角和四元数。下面逐一讲述。

2. 矩阵

矩阵有个非常好的几何解释：矩阵的列表示变换后的基向量位置。因此，如果你知道新坐标系的基向量，把它转换成3*3的矩阵，就得到了用矩阵表示的角位移。

2.1 矩阵形式的优点

可以立即进行向量的旋转：进行矩阵向量乘法 $A x$ ，就能得到变换后向量 $x$ 的位置。后面会介绍，欧拉角没有乘法操作，必须转换成矩阵才能旋转向量。
矩阵的形式被图形API所使用
多个角位移连接很方便：如果知道A关于B的方位M1，B关于C的方位M2，那么A关于C的方位就是M1*M2。
矩阵的逆好求：逆矩阵表示“反”角位移。由于旋转矩阵是正交矩阵，矩阵的逆就是矩阵的转置 $A^{-1}=A^T$ ，计算简单。

2.2 矩阵形式的缺点

矩阵占用了更多的内存：矩阵形式用9个元素表示角位移；后面会介绍，欧拉角只用3个元素，四元数用4个元素。
难于使用：矩阵形式对计算机是友好的，因为无需转换，直接做矩阵向量乘法即可；但是对人类并不直观，普通人没有办法直接从矩阵形式推断出旋转是如何发生的。
矩阵可能是病态的：不是所有矩阵都能表示角位移。矩阵使用9个数，其实只有3个数是必须的。也就是说，矩阵有6个自由度的冗余，也就需要满足6个约束，即，列向量是单位向量且互相垂直。不满足这6个约束的就是病态矩阵。例如，由于浮点精度的限制，大量的矩阵乘法操作可能导致病态矩阵，这种现象称作“矩阵蠕变”。

3. 欧拉角

欧拉（1707~1783）证明了角位移序列等价于单个角位移，即，角位移序列可以描述任意旋转，由此诞生了欧拉角。
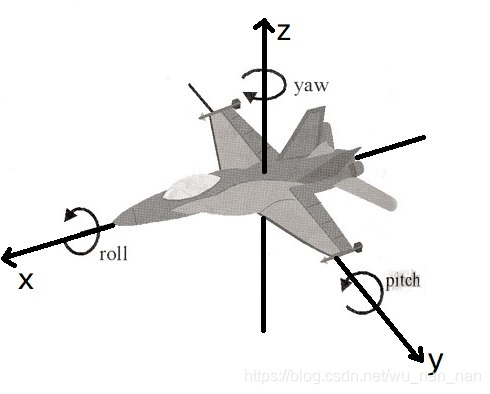
欧拉角的基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。绕哪三个轴？按什么顺序？答案是，任意三个轴，任意顺序（同一个轴不能连续出现，比如x-x-y不行，x-y-x可以）都可以，但最有意义的是使用笛卡尔坐标系并按一定顺序组成的旋转序列。例如，roll-pitch-yaw。
欧拉角示意图

图1 欧拉角示意[1]