均值不等式链的几何证明
这是我们高中时所见到的不等式链的关系,接下来将用几何图形的方法进行证明。
首先,做圆 A,直径 BC,在圆上异于 BC 取一点 D,连接 DA,DB,DC,并做 DE 垂直与 BC 交 BC 与点 E。设 CE = a,BE = b,因为 ▲CDE 与 ▲DBE 相似,从而求出 DE,在▲ADE 中,DA 显然比 DE 大,所以有如下结果。

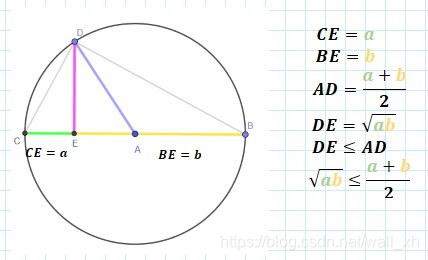
由此,我们可以得出几何平均数和算数平均数之间的关系,之后,我们对上述图形进行改进,使其可以表示四种平均数之间的不等关系。
以 AE 为半径,A 为圆心作圆A’,过点 E,A 分别做 EF,AG 垂直与 AD 交 AD 与 F,交圆A’与点G,通过相似关系可得
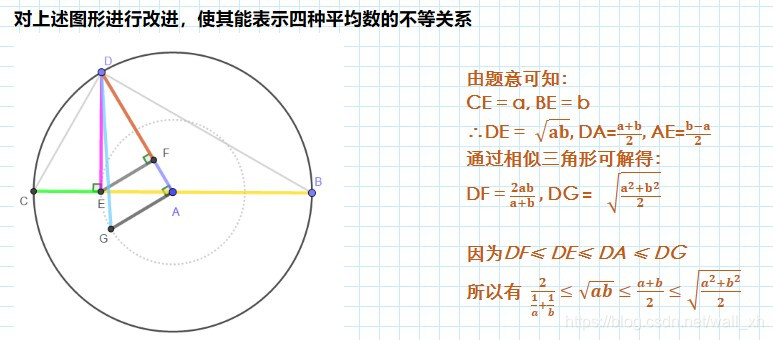


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/44093.html