容抗公式:XC=1/ωC=1/(2πfC) 感抗公式:XL = ωL = 2πfL
计算频率:f=1/2πRC ;计算阻抗:x=1/2πfC
谐振会引起空载电压小于带载电压(获得更大的电压电流),产生过电压。
电容的电压相位滞后电流90°;电感的电流相位滞后电压90°
详情可看: https://zhuanlan.zhihu.com/p/
一、
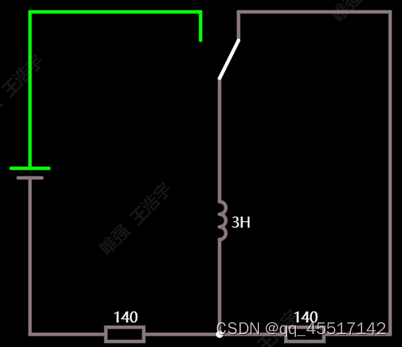
1、电感(RL电路)
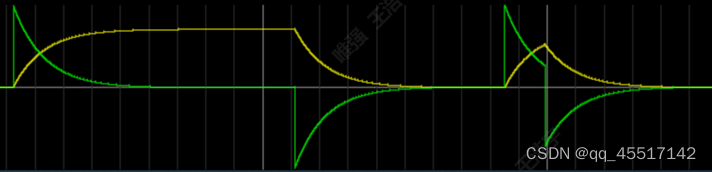
电感会防止电流的突变,使其变化平缓。电感越大,电流变化曲线越平缓。当电感充满电时,开关打向右侧,若电阻小于140,则会使电压大小变小,电流变化变缓(电阻小会减小电流的损耗);若电阻大于140,电流变化剧烈(电阻大增大电流的损耗)
讯享网
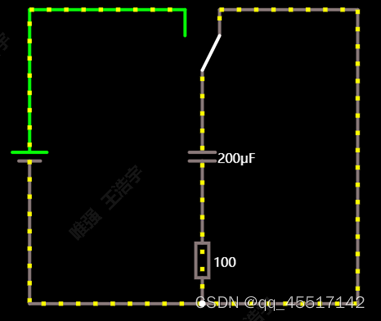
2、电容(RC电路)
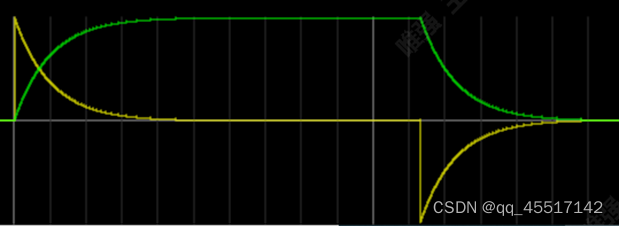
电容会防止电压的突变,使电压变化平缓。电容越大,会使电压变化越小。电阻变大变小只会改变电流的大小,对电压变化无影响。
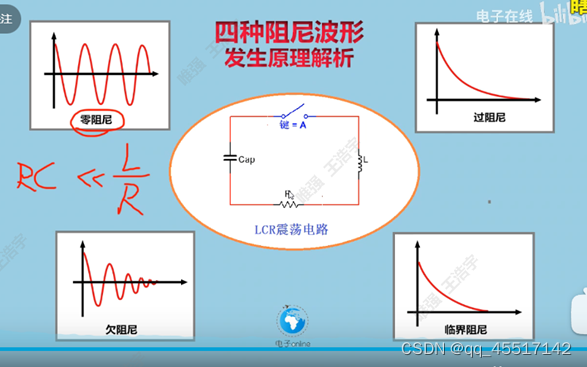
3、LRC电路
分为欠阻尼、过阻尼、零阻尼、临界阻尼这四个状态。会产生谐振,欠阻尼时,由于电阻的作用,会消耗能量,所以会衰减震荡(主要是依靠电阻的大小来控制),处于该状态时,电感给电容充电,直到电感的电流为0,此时电容的电压达到最大值,电容开始放电给电感充电,直到电容的电压为0,此时的电感的电流为最大,不断循环重复这个过程,逐渐衰减为0。
所谓的阻尼就是描述系统达到稳定时过程,当外界施加一个激励时,零阻尼时,系统在平衡状态上下来回振荡;过阻尼时,系统可以一次达到平衡状态,但是需要很长的时间,快速性不够;欠阻尼时,系统在平衡状态处来回振荡,最终达到平衡;临界阻尼时,系统快速准确的达到了平衡状态,这是我们理想的状态。
临界阻尼计算公式:R=2√(L/C) ,
过阻尼:R>2√(L/C),此时电路有不等负实数的两个特征根,非振荡放电过程。
欠阻尼:R<2√(L/C),此时电路有一对共轭复数的两个特征根,振荡放电过程。
零阻尼:R=2√(L/C),此时电路有两个相同的特征根,处于非振荡放电的临界状态。
1、欠阻尼状态
当0<ζ <1时的解为一对实部为负的共轭复根,系统时间响应具有振荡特征,称为欠阻尼状态。
2、临界阻尼
当ζ = 1时的解为一对重实根,此时系统的阻尼形式称为临界阻尼。现实生活中,许多大楼内房间或卫生间的门上在装备自动关门的扭转弹簧的同时,都相应地装有阻尼铰链,使得门的阻尼接近临界阻尼,这样人们关门或门被风吹动时就不会造成太大的声响。
3、过阻尼
当ζ > 1时的解为一对互异实根,此时系统的阻尼形式称为过阻尼。当自动门上安装的阻尼铰链使门的阻尼达到过阻尼时,自动关门需要更长的时间。
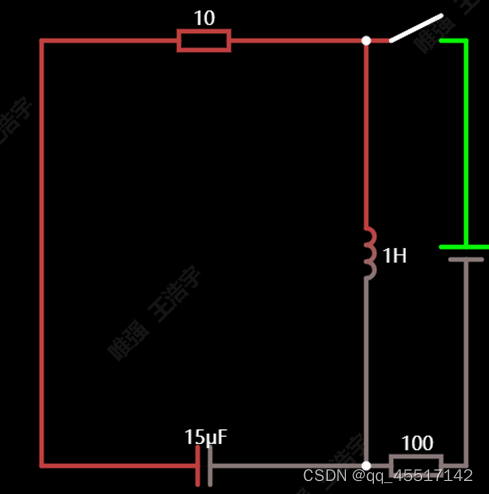

4、串联谐振(产生谐振时电抗Xc+XL=0)
由于电感的电流滞后电压90°,电容的电流超前电压90°,所以其二者放电时产生的电流方向是相对的,又因为二者处于串联状态,所以二者的电流变得相位(方向)相同,所以产生的谐振会更大。(谐振是频率相同,相位相同的波形的叠加)
交变电源的频率越接近电容电感的频率产生的谐振越强(过电压)
串联谐振的谐振频率为: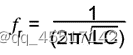
可见以上计算谐振频率公式中不涉及电路中电阻的影响,其可以满足大多数的情况。但是,在低频情况下(使用具有相当大内部电阻的大型电感器)常常不够准确。在这种情况下,需要一个更复杂的公式,其中也要考虑电阻。以下公式可用于低频(较大的内部电阻)计算。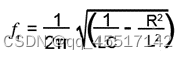
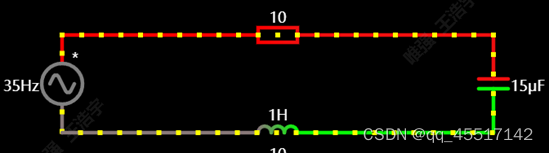

5、并联谐振
由于电感和电容相互并联,其二者放电时产生的电流方向相对,相互抵消(但也会有一定的电流溢出,阻碍电源电流)。当电源的频率接近电感和电容相互并联的频率时,相当于电感和电容相互完全抵消,电路中电感和电容并联的这一部分处于开路状态,此时产生的谐振最小。
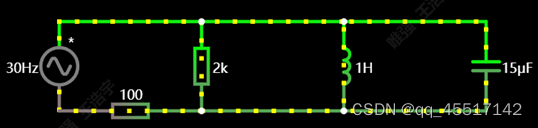
6、高通滤波器(RC)
实际看作电阻分压的原理,当频率无穷大的时候,电容容抗为0,A=输出/输入=1,即输出和输入波形一致;当频率较小的时候,电容的容抗大,由于电阻的分压原理,输出的波形与输入差别较大;当频率为0时,容抗无穷大,断路。
临界点的频率用公式f=1/2πRC计算,大于该频率通过
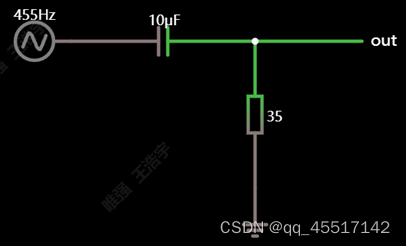
7、低通滤波器(RC)
与高通滤波原理相似,都是利用电阻的分压原理。
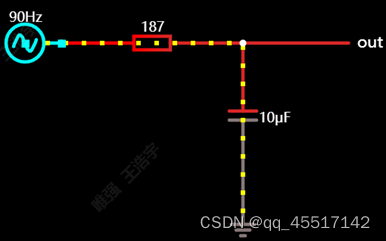
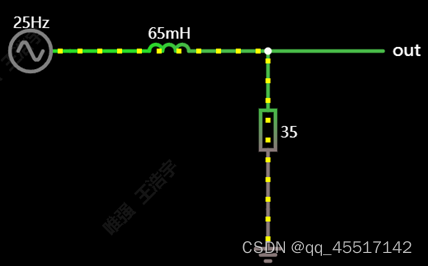
8、高通滤波器(RL)
与RC电路原理相似,同样是电阻分压原理,感抗= XL = ωL = 2πfL。
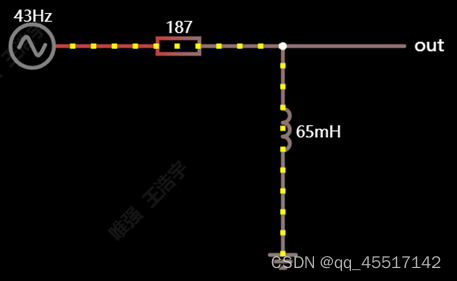
9、低通滤波器(RL)
与RC电路原理相似,同样是电阻分压原理,感抗= XL = ωL = 2πfL。
10、带通滤波器
实质为高通滤波与低通率波的结合,使其输出的频率能够在一定的范围内。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/43661.html