二叉树是一种常见的数据结构，理解二叉树对于理解AVL树、红黑树都有重要意义，索性再重新梳理一下思路，加深印象。本文重点介绍二叉查找树。

1.二叉树与二叉查找树

二叉树（binary tree）是树的一种特殊形式，这种树的每个节点做多只有两个孩子节点，二叉树结构如图：

讯享网
二叉树的树形结构使它很适合扮演索引的角色，因此出现了一种特殊的二叉树—二叉查找树（binary search tree），二叉查找树在二叉树的基础上，又增加了几个条件：
1)如果左子树不为空，则左子树上所有的节点值均小于根节点值；
2）如果右子树不为空，则右子树上所有节点的值均大于根节点的值；
3）左右子树也都是二叉查找树
下图就是一个典型的二叉查找树:

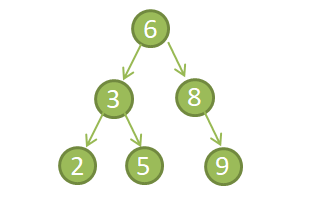
2.二叉树的深度优先遍历

2.1前序遍历

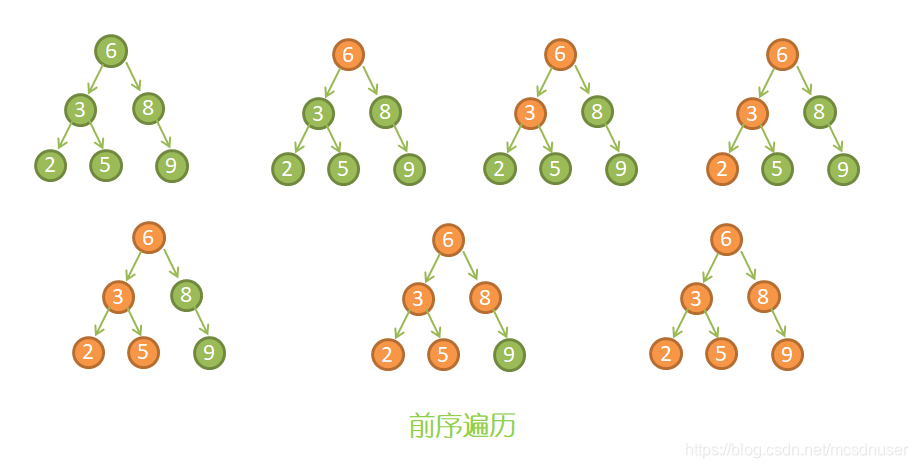
二叉树的前序遍历，输出顺序是根节点、左子树、右子树。示意图如图所示：
1）首先输出根节点6；
2）由于根节点6存在左子节点，输出左子节点3；
3）由于节点3也存在子节点，输出左子节点2；
4）节点2没有左子节点，也没右子节点，回到节点3，输出节点3右子节点5；
5）节点5既没左子节点，也没右子节点，回到节点6，输出节点6的右子节点8；
6）节点8没有左子节点，有右子节点，因此输出节点8的右子节点9；
到此为止，所有节点输出完毕。

2.2中序遍历

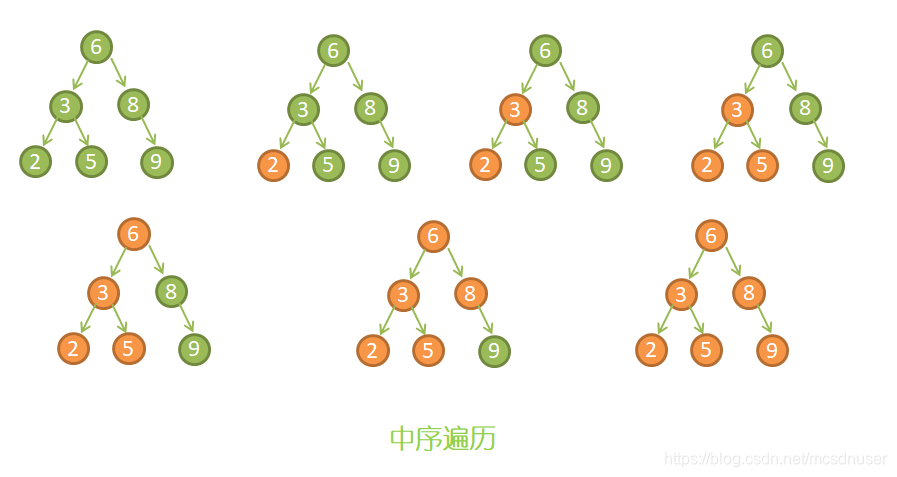
二叉树的前序遍历，输出顺序是左子树、根节点、右子树。示意图如图所示：
1）首先访问左子节点，如果左子节点还有左子节点，则继续深入访问，一直找到不再有左子节点的节点，输出节点2；
2）输出节点2的父节点节点3；
3）输出节点2的右节点节点5；
4）以节点2为根的左子树已输出完毕，这时输出整个二叉树的根节点节点6；
5）由于节点8没左子节点，直接输出节点8；
6）最后输出节点8的右子树节点9；
到此为止，所有节点输出完毕。

2.3后序遍历

二叉树的前序遍历，输出顺序是左子树、右子树、根节点。示意图如图所示：
1）首先访问左子节点，如果左子节点还有左子节点，则继续深入访问，一直找到不再有左子节点的节点，输出节点2；
2）输出节点2的右节点节点5；
3）输出节点2的父节点节点3；
4）以节点2为根的左子树已输出完毕，开始查找根节点的右子树，节点8没有左子节点，但有右子节点，输出右子节点9；
5）输出右子节点的父节点节点8；
6）最后输出节根节点节点6；
到此为止，所有节点输出完毕。

3.配套代码

三种遍历方式，用递归实现会非常简单。

/ * 二叉查找树 */ public class BinarySearchTree { 
    //根节点 TreeNode root; / * 构建二叉查找树 * @param node * @param data */ public void createTree(TreeNode node, int data){ 
    if(root == null){ 
    root = new TreeNode(data); }else{ 
    if(data < node.data){ 
    if(node.left == null){ 
    node.left = new TreeNode(data); }else{ 
    createTree(node.left,data); } }else{ 
    if(node.right == null){ 
    node.right = new TreeNode(data); }else{ 
    createTree(node.right,data); } } } } / *二叉树前序遍历 * @param node */ public void preOrderTraversal(TreeNode node){ 
    if(node == null){ 
    return ; } System.out.println(node.data); preOrderTraversal(node.left); preOrderTraversal(node.right); } / *二叉树中序遍历 * @param node */ public void middleOrderTraversal(TreeNode node){ 
    if(node == null){ 
    return ; } middleOrderTraversal(node.left); System.out.println(node.data); middleOrderTraversal(node.right); } / *二叉树后序遍历 * @param node */ public void postOrderTraversal(TreeNode node){ 
    if(node == null){ 
    return ; } postOrderTraversal(node.left); postOrderTraversal(node.right); System.out.println(node.data); } } / * 二叉树节点 */ class TreeNode { 
    //节点数据 int data; //左子树 TreeNode1 left; //右子树 TreeNode1 right; public TreeNode(int data) { 
    this.data = data; } } 

测试类：

讯享网public static void main(String[] args){ 
    int[] arr = { 
   10,2,3,1,11}; BinarySearchTree tree = new BinarySearchTree(); for(int data : arr){ 
    tree.createTree(tree.root,data); } //前序遍历 System.out.println("前序遍历"); tree.preOrderTraversal(tree.root); //中序遍历 System.out.println("中序遍历"); tree.middleOrderTraversal(tree.root); //后序遍历 System.out.println("后序遍历"); tree.postOrderTraversal(tree.root); }