解决一个回溯问题,实际上就是一个决策树的遍历过程,需要考虑的三个问题:
- 路径:也就是已经做出的选择。
- 选择列表:当前可以做的选择。
- 结束条件:到达决策树底层,无法再做出选择条件。
回溯算法的框架:
result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径,选择列表) 撤销选择讯享网
全排序问题
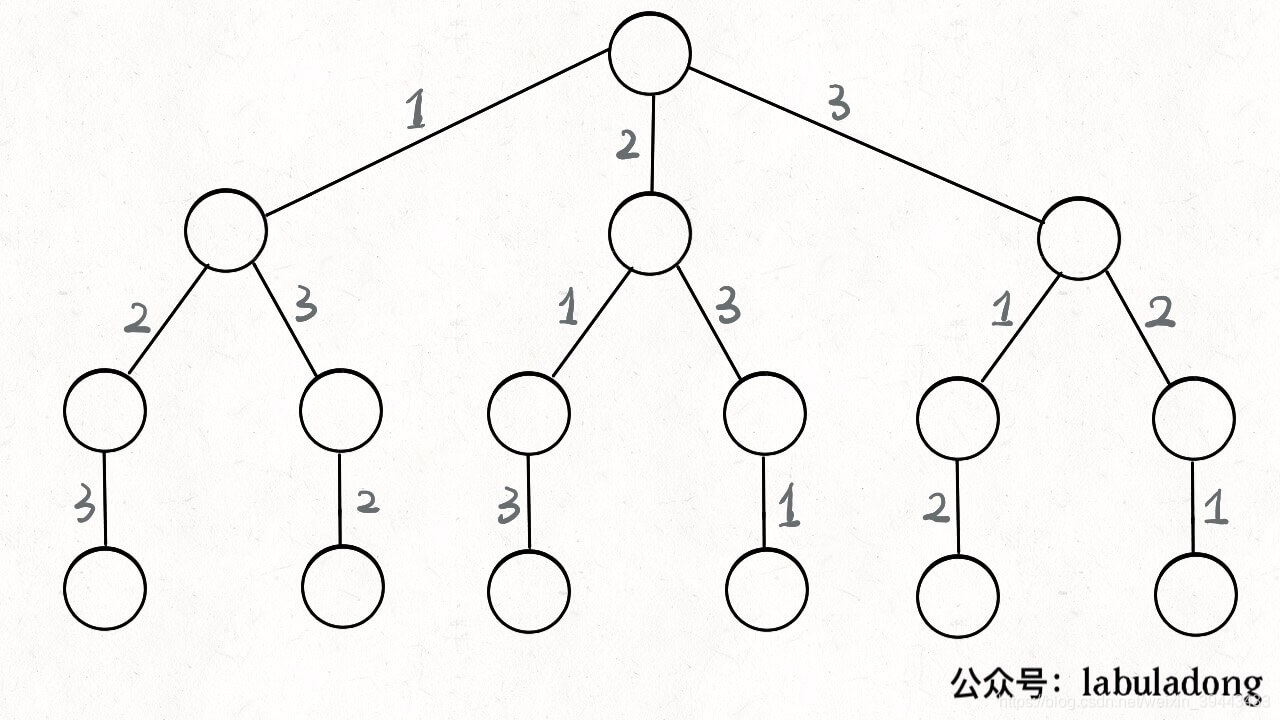
我们通常会先固定第一个数,然后是从剩下的里面选择一个固定第二位,最后是剩下的作为第三位,这其实就是回溯算法,而这个过程可以用一棵树来表示,这棵树就是决策树。
路径:就是每次固定的数
选择列表:当前还可以选择的树
结束条件:遍历到树的底层--选择列表为空的时候

所定义的backtrack函数其实就像一个指针,在决策树上游走。
讯享网 private List<List<Integer>> res = new LinkedList<>(); // 主函数,输入一组不重复的数字,返回它们的全排序 public static List<List<Integer>> permute(int[] nums){ // 记录【路径】 LinkedList<Integer> track = new LinkedList<>(); backtrack(nums, track); return res; } // 路径:记录在track中 // 选择列表:nums中不存在于track的那些元素 // 结束条件:nums中的元素全部在track中出现 public static void backtrack(int[] nums, LinkedList<Integer> track){ // 触发结束条件 if (track.size() == nums.length){ res.add(new LinkedList<>(track)); return; } for(int i = 0; i < nums.length; i ++){ // 排除不合法的选择 if (track.contains(nums[i])){ continue; } // 做选择 track.add(nums[i]); // 进入下一层决策树 backtrack(nums,track); // 取消选择 track.removeLast(); } }
回溯算法就是个多多叉树遍历的问题,关键是在前序遍历和后序遍历的位置做一些操作:
def backtrack(...): for 选择 in 选择列表: 做选择 backtrack(...) 撤销选择写backtrack函数时,需要维护走过的路径和当前可以做的选择列表,当触发结束条件时,将路径计入结果集。
参考书籍:《labuladong的算法小抄》

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/38901.html