2025年Codeforces 1427E. Xum 思维+构造+数论

科技前沿 • 2025-02-21 21:32 • 阅读 34

大家好，我是讯享网，很高兴认识大家。

题目链接
一开始的时候给我们一个X 奇数现在我们可以有两种操作
在这里插入图片描述
讯享网
每次构造后新构造的数会放入到序列中可以继续使用
现在要我们构造出来使得序列中出现 1

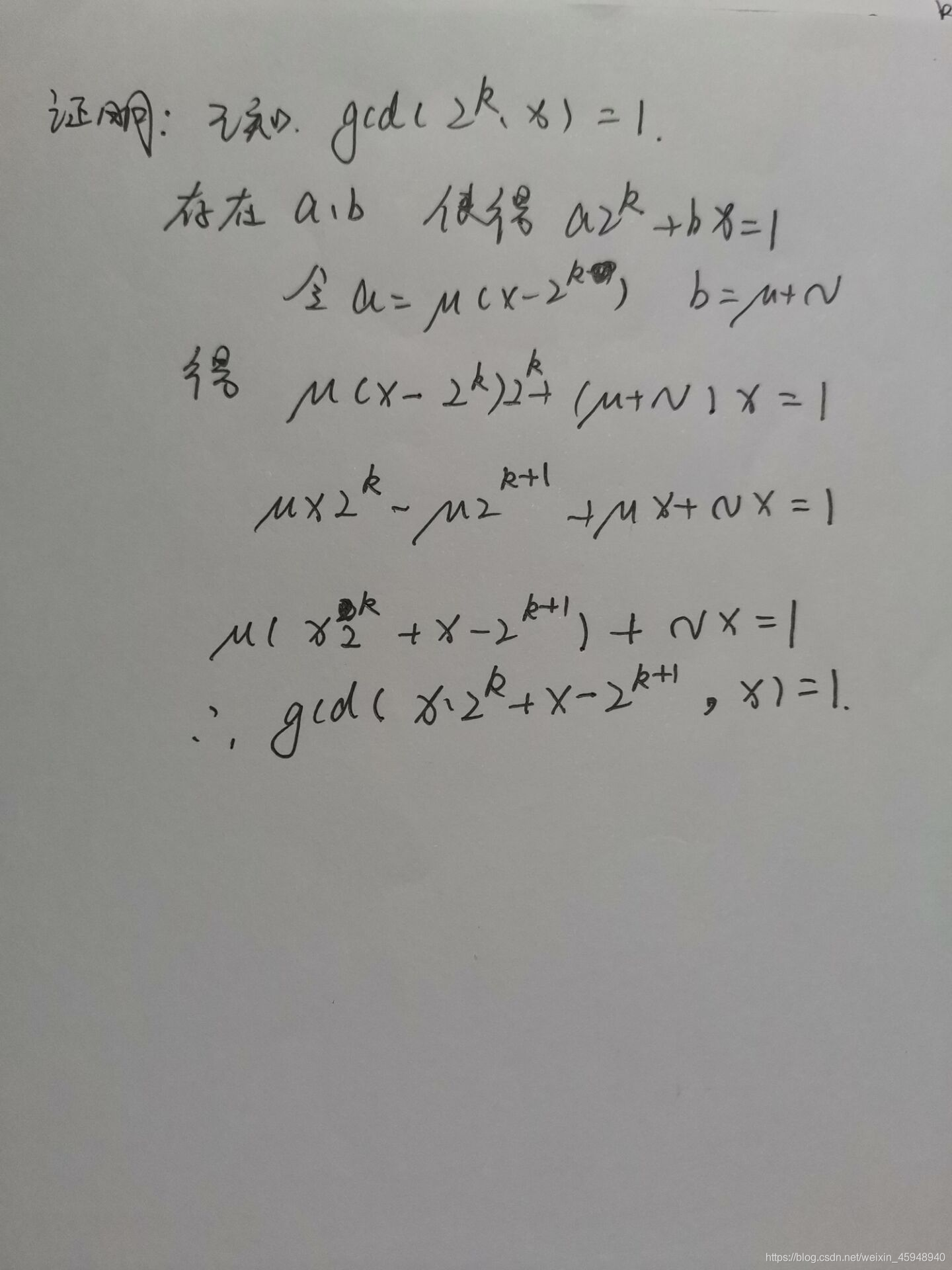
在这里插入图片描述

两种操作是取两个数做加法或者做异或
那么很方便的我们可以得到一个数为X * 2^k
X+X=2X
2X+2X=4X
4X+4X=8X
我们继续观察， 2^k 相当于把X 的二进制模式整体移动k位
那么取一个临界点继续观察令k为最大的 2^k <x
那么我们可以每次消去一个数的最高位的1
假设我们恰好消去它，继续观察发现也就是说 x异或2^kx 总是互质的
在这里插入图片描述
也就是说2^(k) *x +x - 2^(k+1) 与 x 互质

gcd(a, b)=gcd (a, b-a)

那么我们就有了与初始x 互质的一个数 y
既然x y 互质不妨使用exgcd 求得一组ax-by=1
ax=by+1 如果b是偶数那么ax异或by 一定可以得到1
如果b不是偶数我们可以调整系数使他变为偶数
然后就是龟速乘记录ax by的过程
操作op=1 或者0 代表着运算符号种类
遍历一次vector 就OK

 #include<bits/stdc++.h> #include<stdlib.h> #include<algorithm> #include<stdio.h> #include<string.h> #include<queue> #include<time.h> #include <cstdio> #include <iostream> #include <vector> #define ll long long #define int long long #define inf 0x3f3f3f3f #define mods  #define modd  #define PI acos(-1) #define fi first #define se second #define lowbit(x) (x&(-x)) #define mp make_pair #define pb push_back #define si size() #define E exp(1.0) #define fixed cout.setf(ios::fixed) #define fixeds(x) setprecision(x) #define IOS ios::sync_with_stdio(false);cin.tie(0) using namespace std; ll gcd(ll a,ll b){ 
   if(a<0)a=-a;if(b<0)b=-b;return b==0?a:gcd(b,a%b);} template<typename T>void read(T &res){ 
   bool flag=false;char ch;while(!isdigit(ch=getchar()))(ch=='-')&&(flag=true); for(res=ch-48;isdigit(ch=getchar());res=(res<<1)+(res<<3)+ch - 48);flag&&(res=-res);} ll lcm(ll a,ll b){ 
   return a*b/gcd(a,b);} ll qp(ll a,ll b,ll mod){ 
   ll ans=1;if(b==0){ 
   return ans%mod;}while(b){ 
   if(b%2==1){ 
   b--;ans=ans*a%mod;}a=a*a%mod;b=b/2;}return ans%mod;}//快速幂% ll qpn(ll a,ll b, ll p){ 
   ll ans = 1;a%=p;while(b){ 
   if(b&1){ 
   ans = (ans*a)%p;--b;}a =(a*a)%p;b >>= 1;}return ans%p;}//逆元 (分子*qp(分母,mod-2,mod))%mod; ll exgcd(ll a,ll b,ll &x,ll &y){ 
    if (!b){ 
    x=1,y=0; return a; } ll ans=exgcd(b,a%b,y,x); y-=(a/b)*x; return ans; } struct pe{ 
    ll x; ll op; ll y; }; vector<pe>ans; void mulit(ll a,ll b) { 
    ll res = -1; while(b) { 
    if(b & 1) { 
    if(res == -1) res = a; else { 
    ans.pb({ 
   res, 0, a}); res += a; } } ans.pb({ 
   a, 0, a}); a += a; b >>= 1; } } signed main(){ 
    ll x; read(x); ll cnt=1; while(2*cnt<x){ 
    ans.pb({ 
   cnt*x,0,cnt*x}); cnt=cnt*2; } ans.pb({ 
   x,1,cnt*x}); // 得到y ll y=x^(cnt*x); ll a,b; exgcd(x,y,a,b); b=-b; if(a<=0) { 
    ll bei =(-a)/y +1; a +=y*bei; b +=x*bei; } if(b%2==1)a+= y, b += x; mulit(x,a); mulit(y,b); ans.pb({ 
   a * x, 1, b * y}); printf("%d\n",ans.size()); for(auto v : ans){ 
    printf("%lld",v.x); if(v.op==0){ 
    printf(" + "); } else{ 
    printf(" ^ "); } printf("%lld\n",v.y); } }

讯享网

2025年Codeforces 1427E. Xum 思维+构造+数论

相关推荐