第3课 ： 关于离散随机变量的更多信息
Probability generating functions (pgf, 概率生成函数)
假设X是一个离散型随机变量，只取非负整数值。X的概率生成函数(pgf)为：
注:G(
) 是X的概率质量函数（概率分布函数）G()=
泊松分布的概率生成函数：
泊松分布概率生成函数 pgf ：
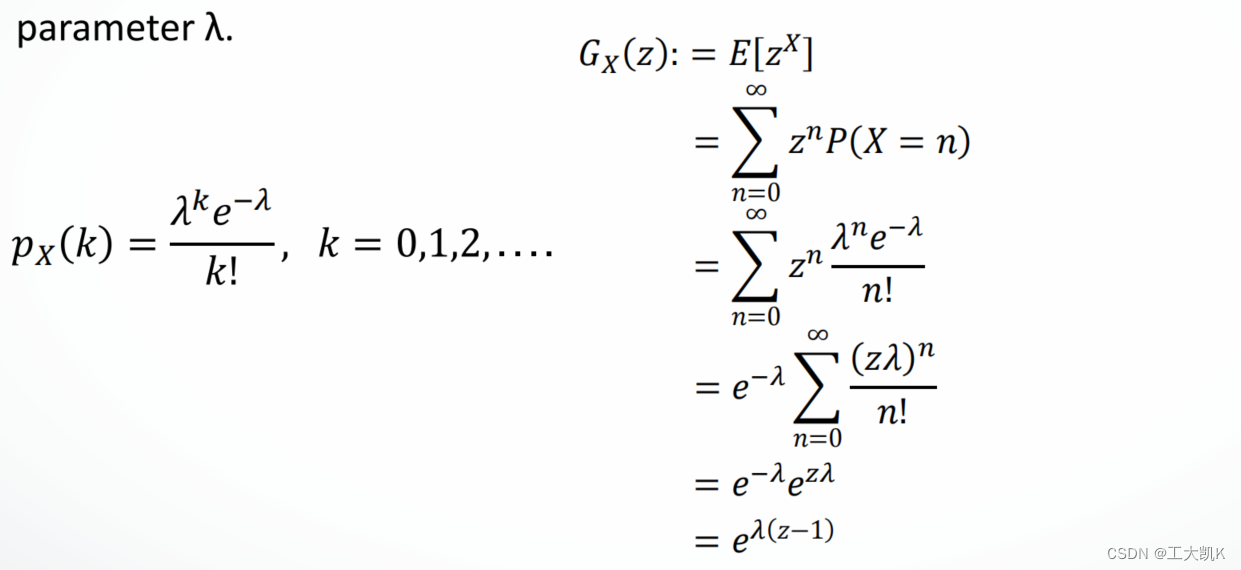
概率生成函数的重要性质：
1： 独立随机变量之和的概率生成函数pgf 等于 各个独立随机变量概率生成函数pgf 的 乘积 。(因分解特性factorization property)
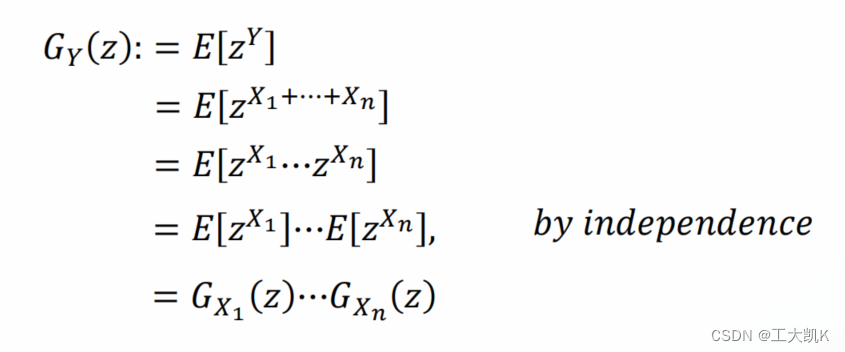
重要性质的相关例子：
X (参数为) 和 W（参数为）是相互独立的泊松分布随机变量 Y = X+Y ，求Y的概率生成函数
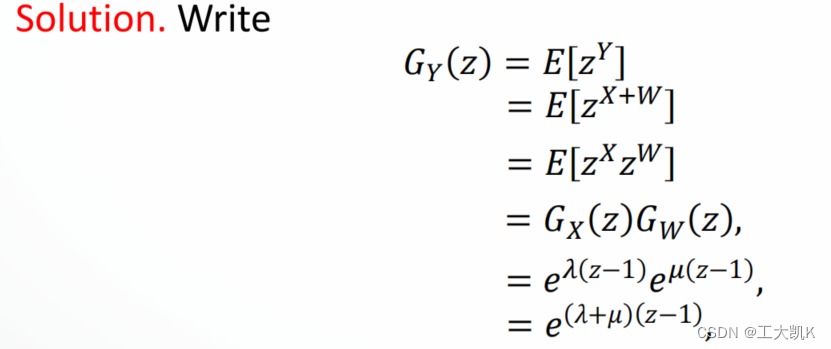
从概率生成函数pgf 恢复 概率质量函数（概率分布函数）
1. 概率生成函数的一般展开式
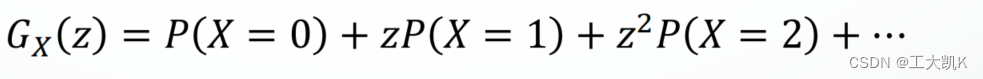
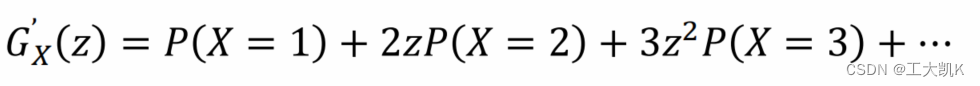
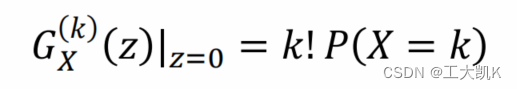
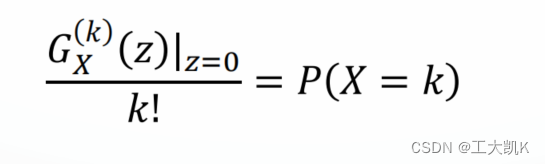
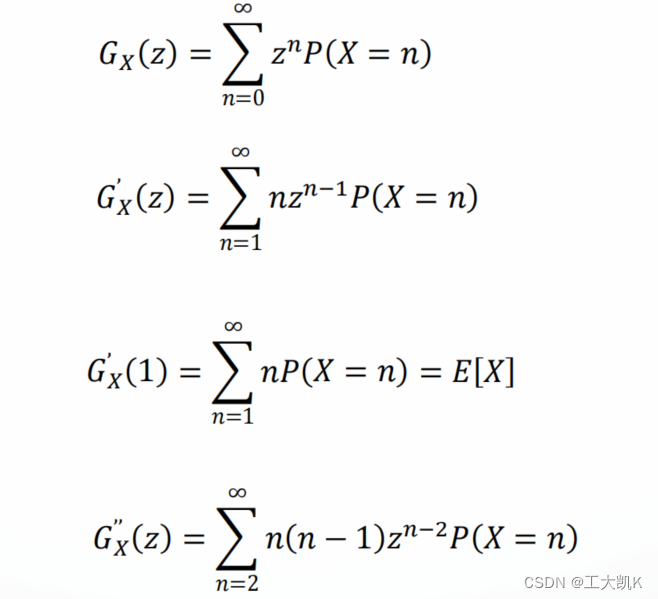
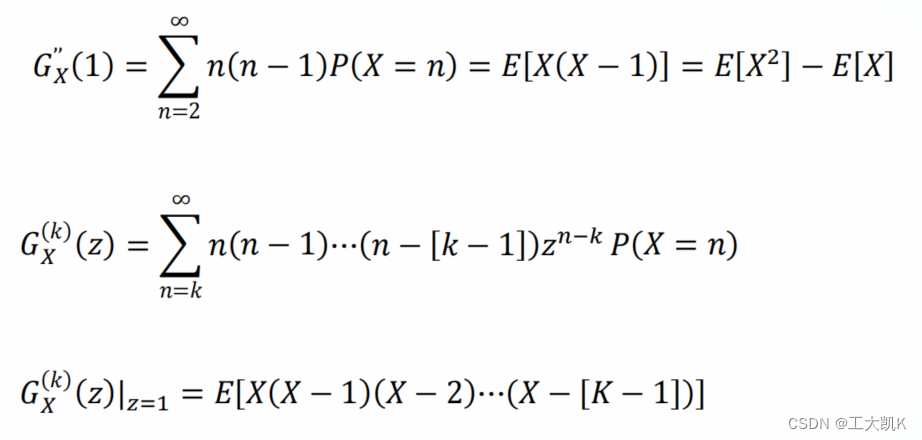
binomial random variable（二项式随机变量）
二项分布的概率质量函数（概率分布函数）
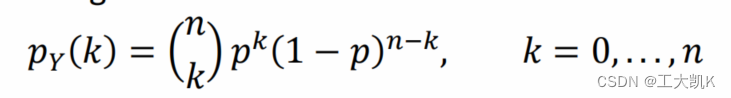
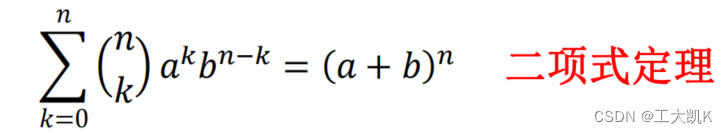
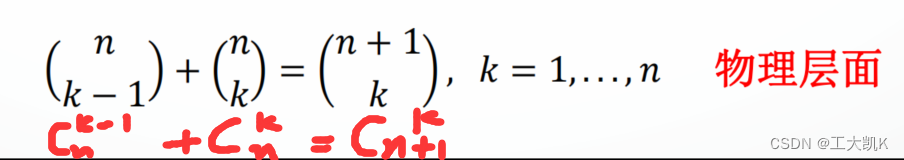
当n很大、p很小的时候，二项分布可以近似看成以参数=np的泊松分布
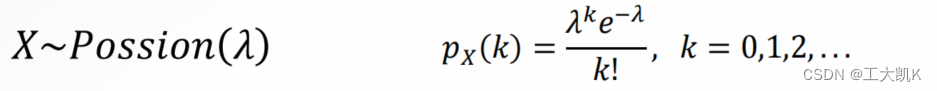
二项分布概率生成函数pgf：
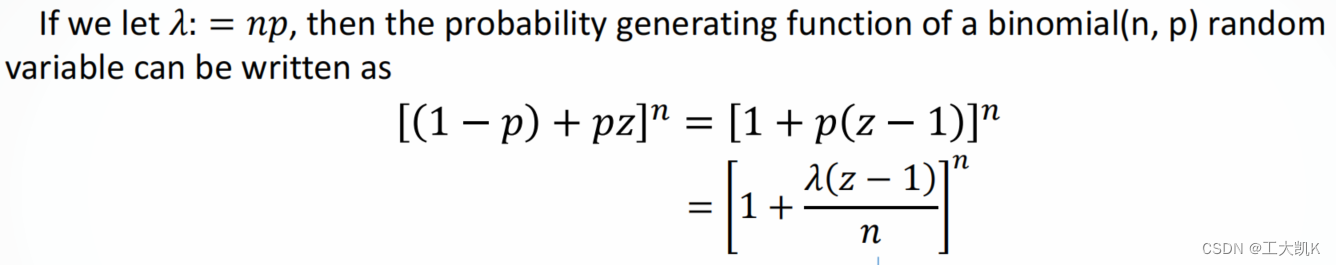
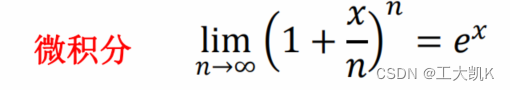
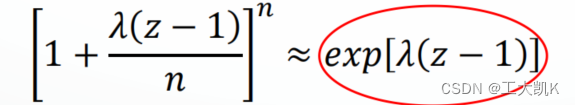
因为我们可以通过概率生成函数恢复概率质量函数（概率分布函数）（使用求导 z=0的方法），所以若两个随机变量的概率生成函数近似的话，可以得出两个随机变量的概率分布也是近似的。
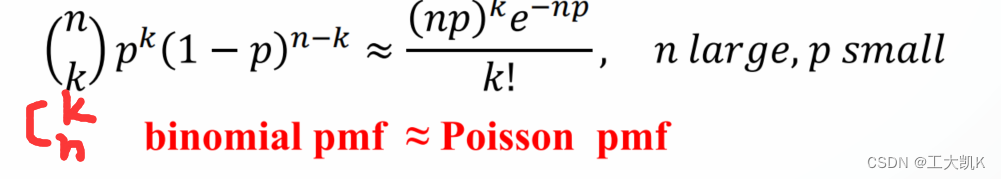
弱大数定理（The weak law of large numbers）WLLN
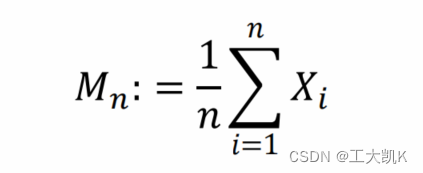
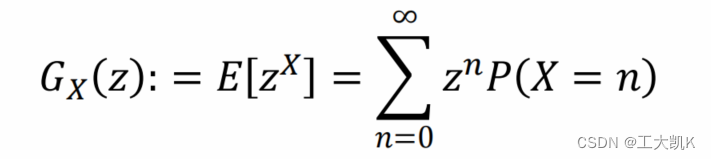
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请联系我们，一经查实，本站将立刻删除。
如需转载请保留出处：https://51itzy.com/kjqy/22921.html