2025年机器学习逻辑回归。

科技前沿 • 2025-03-13 20:28 • 阅读 60

大家好，我是讯享网，很高兴认识大家。

逻辑回归最经典的分类算法

有监督机器学习
线性回归：预测一个连续的值
逻辑回归：预测一个离散的值

逻辑回归的引入

良性肿瘤 and 恶性肿瘤
有一家医院希望我们能开发出一款分类器，可以通过数据分析出一块肿瘤到底是良性的，还是恶性的。
在这里插入图片描述
讯享网

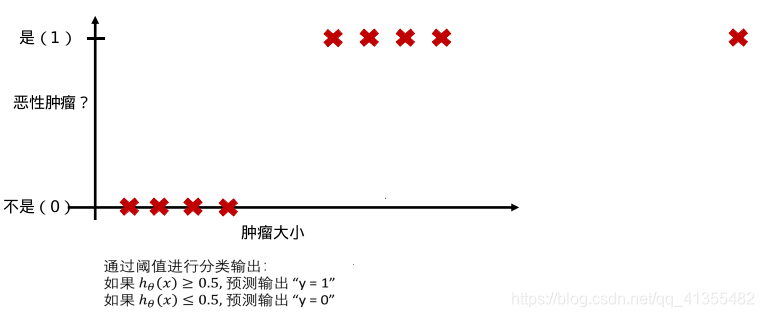
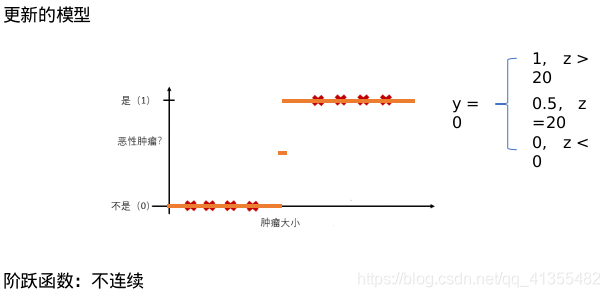
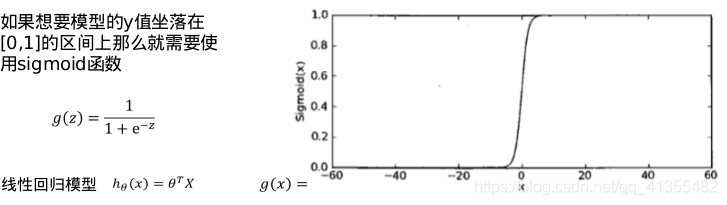
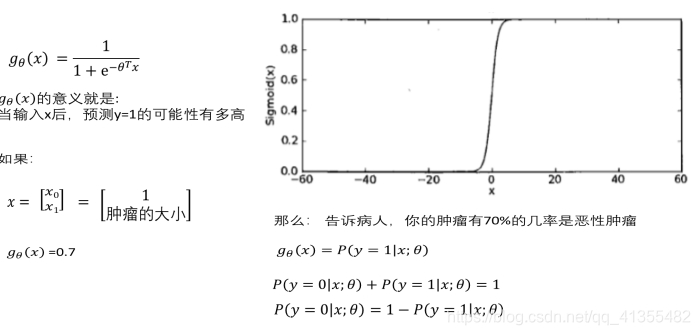
当我们要做二分类的时候，我们一般只希望得到两个值 y = 0 或 1。但是，线性回归得到的值是在一个范围内的连续值，而且可能远 > 1 或远 < 0。这样会给分类带来困难。

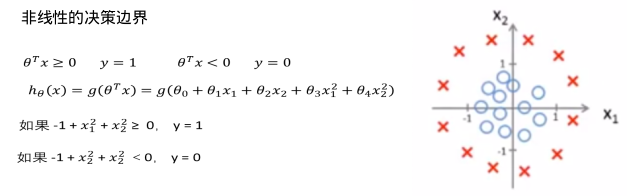
熵的引入

熵的意义：
热力学上：熵是一种测量分子不稳定的指标，分子运动越不稳定，熵就越大
信息论（香农）：熵是一种测量信息量的单位，信息熵，包含的信息越多，熵就越大。
机器学习:熵是一种测量不确定性的单位，不确定性越大，概率越小，熵就越大！
在这里插入图片描述

SoftMax

有一种逻辑回归的一般形式，叫做Softmax回归，能让你在试图识别某一分类中做出预测，或者说多分类的一种，不只是识别两个分类。C表示你的输入会被分入的类别总个数。
在这里插入图片描述
逻辑回归和SoftMax的区别。
逻辑回归主要是用来做二分类的，Softmax主要是用来做多分类的。
SoftMax回归将logistic激活函数推广到C类，而不仅仅是两类，如果C=2，那么softmax实际上就是逻辑回归。

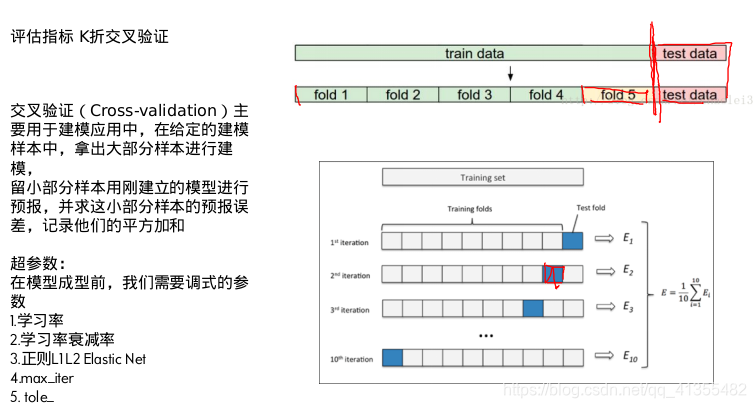
评估指标 K折交叉验证

在这里插入图片描述
正例和负例
对于二分类问题，可将样例根据其预测结果分为正例（Positive）和负例（Negative）

真例和假例（便于理解）
对于二分类问题，可将样例根据其预测类别(预测的对不对)分为真例（True）和假例（False）

查准率和查全率
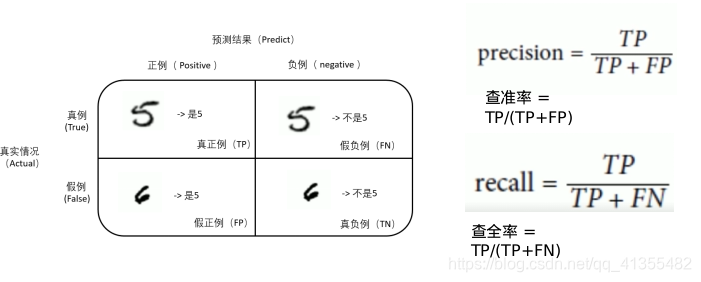
在这里插入图片描述

做一个逻辑回归的例子

代码实现如下：

import numpy as np from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split,GridSearchCV import matplotlib.pyplot as plt iris=datasets.load_iris() X=iris['data'] Y=iris['target'] X_train,X_test,Y_train,Y_test=train_test_split(X,Y,test_size=0.2) # X_train=iris['data'][:120] # Y_train=iris['target'][:120] # X_test=iris['data'][120:] # Y_test=iris['target'][120:] param_grid={'tol':[1e-4,1e-3,1e-2], 'C':[0.4,0.6,0.8] } log_reg=LogisticRegression(multi_class="ovr",solver= "sag",max_iter=10000) # log_reg.fit(X_train,Y_train) grid_search=GridSearchCV(log_reg,param_grid,cv=3,iid=True) grid_search.fit(X_train,Y_train) print("train_score:",grid_search.score(X_train,Y_train)) print("test_score:",grid_search.score(X_test,Y_test)) # Y_train_predict=log_reg.predict(X_train) # print("train_score",log_reg.score(X_train,Y_train)) # print("text_score",log_reg.score(X_text,Y_text))

讯享网

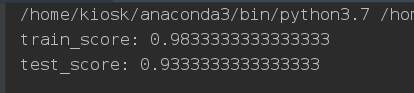
在这里插入图片描述
我们训练集的分数和测试集分数都还是比较高的。