利用泊松变形实现平面浅浮雕生成

参考论文：Zhang Y W , Zhou Y Q , Li X L , et al. Bas-Relief Generation and Shape Editing through Gradient-Based Mesh Deformation[J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(3):328-338.

这篇论文主要利用通过求解泊松方程来实现浅浮雕的生成，这是我读研以来实现的第二篇论文，实现的过程中由于数学知识的不足还是遇到了不少的障碍。

准备

1. pmp-library :该类库提供了简便的三角形网格框架，除了基本的三角形网格数据结构之外，还提供了许多网格处理有关的算法，如网格简化、remesh等，我在体验之后感到的缺点主要是虽然该库的矩阵系统是基于Eigen的，但是他的矩阵与Eigen的并不兼容，并且他提供的矩阵初始化很麻烦，我在github上和作者反映了这个问题，他说今后会考虑将矩阵系统整个换成Eigen的。
2. Eigen:十分有名的C++类库了，提供可线性代数，矩阵和矢量运算以及数值分析等算法。

预处理阶段

1. 准备一个三角形网格模型
2. 将其放入maya中进行编辑，如图所示

讯享网

​ 随后手动编辑取一半作为输入，如图所示

3. 在代码中调用pmp中提供的remesh方法对网格进行remesh，remesh的参数取网格的平均边长

   / * remesh，取网格的平均边长作为参数 * @param mesh * @return */ Scalar remeshing(SurfaceMesh &mesh) { cout << "正在进行remesh" << endl; SurfaceRemeshing remesh(mesh); Scalar avg_scalar = 0; for (auto e : mesh.edges()) { avg_scalar += mesh.edge_length(e); } avg_scalar /= mesh.n_edges(); cout << "average edge length = " << avg_scalar << endl; remesh.uniform_remeshing(avg_scalar); cout << "remesh完成" << endl; cout << "vertices:" << mesh.n_vertices() << ", edges:" << mesh.n_edges() << ", faces:" << mesh.n_faces() << endl; return avg_scalar; } 

   
   讯享网
4. 网格简化，调用pmp的网格简化算法，将面片数大于一定值的网格进行简化

   讯享网/ * 简化网格，当三角形面片数量大于门限值时对网格进行简化 * @param mesh * @param avg_scalar * @return */ int simplification(SurfaceMesh &mesh, const Scalar avg_scalar) { cout << "正在进行simplification" << endl; SurfaceSimplification simplification1(mesh); simplification1.initialize(5, avg_scalar, 10, 10, 0.001); int n = mesh.n_vertices() <= 10e3 ? mesh.n_vertices() : 5e3 + mesh.n_vertices() / 2; cout << "simplify之后的顶点数量为：" << n << endl; simplification1.simplify(n); cout << "simplify完成" << endl; cout << "vertices:" << mesh.n_vertices() << ", edges:" << mesh.n_edges() << ", faces:" << mesh.n_faces() << endl; return 0; } 

利用泊松变形(Poison Deformation)生成浅浮雕

泊松等式

具有狄利克雷条件的泊松等式定义如(1)式：
$${\nabla }^{2}f=\nabla \cdot \mathbf{w},f{|}_{\partial \Omega }=f^{\ast }{|}_{\partial \Omega }\text{\hspace{1em}(1)}$$
其中$f$是一个未知的标量函数，$\mathbf{w}$是一个梯度矢量场，$f^{\ast }$为边界约束，${\nabla }^2$为拉普拉斯算子，即梯度的散度，而$\nabla \cdot \mathbf{w}$ 为梯度矢量场$\mathbf{w}=(w_x,w_y,w_z)$的散度，泊松等式的意义在于，一个网格的拉普拉斯坐标值等于其网格面片的梯度场的散度，也就是说我们可以通过操纵网格的梯度场反过来去求出对应网格顶点的位置从而达到变形的目的。表示成矩阵形式就是：
$$Lx=b\text{\hspace{1em}(2)}$$
其中L为三角形网格的拉普拉斯矩阵，可以通过下式求得：
$$L_{ij}=\{\begin{array}{ll}\sum _{(i,k)\in E}{w}_{ik}& i=j\\ -w_{ij}& (i,j)\in E\\ 0& otherwise\end{array},\text{\hspace{1em}(3)}$$
i和j代表矩阵的横纵坐标，$w_{ij}=\frac{1}{2}(\cot \alpha +\cot \beta )$,

b为带有狄利克雷约束的矢量，由$div\mathbf{w}(v_i)$组成，由下式计算：
$$divw=\sum _{T_j\in N_T(v_i)}\nabla \varphi (v_i{)}^T|T_j\cdot w(T_j)\cdot A(T_j)\text{\hspace{1em}(4)}$$
如果定义$f_i,f_j,f_k$为三角形面片三个顶点的值（可以为坐标值），$A(T_j)$为三角形面片的面积，${\varphi }_i$为定义在三角形三个顶点上的帽函数（可以理解为三组基对应直角坐标系的xyz轴），那么三角形面片之内的任意一点可以表示为：
$$f(v)=f_i{\varphi }_i+f_j{\varphi }_j+f_k{\varphi }_k\text{\hspace{1em}(5)}$$
注意$f_i$为标量而${\varphi }_i$为矢量，那么三角形的梯度就可表示为：
$$\nabla f(v)=f_i\nabla {\varphi }_i+f_j\nabla {\varphi }_j+f_k\nabla {\varphi }_k\text{\hspace{1em}(6)}$$
由于中心坐标的性质，$\nabla {\varphi }_i+\nabla {\varphi }_j+\nabla {\varphi }_k=0$将$\nabla {\varphi }_i$用$\nabla {\varphi }_j,\nabla {\varphi }_k$来表示，那么
$$\nabla f(v)=(f_j-f_i)\nabla {\varphi }_j+(f_k-f_i)\nabla {\varphi }_k\text{\hspace{1em}(7)}$$
$\nabla {\varphi }_i,\nabla {\varphi }_j,\nabla {\varphi }_k$可以由下式得出：

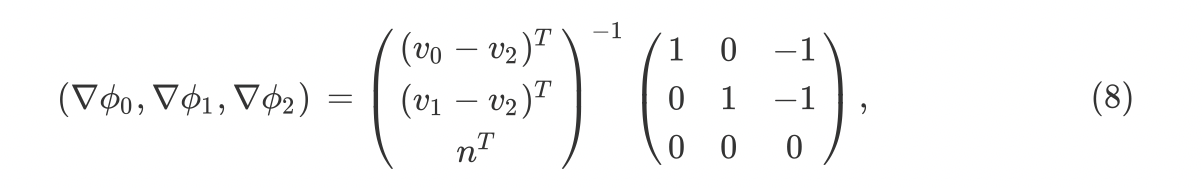
该式子的推导可以在[2]中找到。

数值求解

通过上面的数学公式，我们可以对泊松等式进行求解，在该问题中，在变换时仅将z坐标的值做约束，xy坐标值不约束，所以上式的$f_i$由三角形面片上各个顶点的z坐标值，确定好整个三角形网格的边界后，将边界顶点的z坐标值设置到基平面上（由于本文在实现时并没有输入基平面，所以简单将基平面设置为xoy平面，即设置z=0），然后通过最小二乘法对方程进行求解

/ * 获取梯度场 * @param mesh * @param face * @param point * @return */ Eigen::Vector3f get_gradient_Phi(const SurfaceMesh &mesh, const Face &face, const Vertex &point) { vector<Point> points; int index = 0, i = 0; for (auto v : mesh.vertices(face)) { if (v == point) index = i; Point p = mesh.position(v); if(mesh.is_boundary(v)) p[1] = 0; points.push_back(p); i++; } assert(points.size() == 3); Eigen::Matrix3f m_left, m_right; m_right << 1, 0, -1, 0, 1, -1, 0, 0, 0; Point v1 = points[0] - points[2]; Point v2 = points[1] - points[2]; Normal n = SurfaceNormals::compute_face_normal(mesh, face); Eigen::Vector3f ev1, ev2, en; ev1 << v1[0], v1[1], v1[2]; ev2 << v2[0], v2[1], v2[2]; en << n[0], n[1], n[2]; m_left << ev1.transpose(), ev2.transpose(), en.transpose(); Eigen::Matrix3f res = m_left.inverse() * m_right; return res.col(index); } Eigen::Vector3f getGradientField(const SurfaceMesh &mesh, const Face &f) { Vertex vi, vj, vk; int i = 0; for (auto v : mesh.vertices(f)) { if (i == 0) vi = v; else if (i == 1) vj = v; else vk = v; i++; } Point pi, pj, pk; pi = mesh.position(vi); pj = mesh.position(vj); pk = mesh.position(vk); if(mesh.is_boundary(vi)) pi[1] = 0; if(mesh.is_boundary(vj)) pj[1] = 0; if(mesh.is_boundary(vk)) pk[1] = 0; Eigen::Vector3f vpi, vpj, vpk; vpi << pi[0], pi[1], pi[2]; vpj << pj[0], pj[1], pj[2]; vpk << pk[0], pk[1], pk[2]; Scalar vpij = vpj[1] - vpi[1]; Scalar vpik = vpk[1] - vpi[1]; Eigen::Vector3f v1 = vpij * get_gradient_Phi(mesh, f, vj); Eigen::Vector3f v2 = vpik * get_gradient_Phi(mesh, f, vk); Eigen::Vector3f w = v1 + v2; return w; } / * 生成目标矩阵场2n*n * @param mesh * @return */ Eigen::MatrixXf generate_b(SurfaceMesh &mesh) { cout << "正在生成目标矩阵场" << endl; const int n = mesh.n_vertices(); Eigen::VectorXf divw = Eigen::VectorXf::Zero(n); int idx = 0; //n*3 for (auto v : mesh.vertices()) { Scalar res = 0; for (auto f : FaceNeighbors(&mesh, v)) { Point p[3]; Scalar area = 0; if(mesh.is_boundary(f)) { int i = 0; for(auto vv: mesh.vertices(f)) { p[i] = mesh.position(vv); if(mesh.is_boundary(vv)) p[i][1] = 0; i++; } area = triangle_area(p[0], p[1], p[2]); } else { area = triangle_area(mesh, f); } Eigen::Vector3f grad_ti = get_gradient_Phi(mesh, f, v); res += area * grad_ti.transpose() * getGradientField(mesh, f); } divw.row(idx++) << res; } cout << "目标矩阵场生成完毕" << endl; return divw; } / * 生成拉普拉斯矩阵 * @param mesh * @return */ SparseMatrixType generate_Laplace(const SurfaceMesh &mesh) { cout << "正在生成拉普拉斯矩阵" << endl; int vn = mesh.n_vertices(); int count0 = 0; vector<int> begin_N(vn); for (auto v : mesh.vertices()) { begin_N[v.idx()] = count0; count0 += mesh.valence(v) + 1; } typedef Eigen::Triplet<Scalar> T; vector<T> tripletList(count0); //n*n for (auto v : mesh.vertices()) { int i = 0; Scalar sum_weight = 0; for (auto nei_v : VertexNeighbors(&mesh, v)) { Edge e = mesh.find_edge(v, nei_v); Scalar weight = 0.5 * cotan_weight(mesh, e); tripletList[begin_N[v.idx()] + i + 1] = T(v.idx(), nei_v.idx(), -weight); i++; sum_weight += weight; } tripletList[begin_N[v.idx()]] = T(v.idx(), v.idx(), sum_weight); } Eigen::SparseMatrix<Scalar> Ls(vn, vn); Ls.setFromTriplets(tripletList.begin(), tripletList.end()); cout << "拉普拉斯矩阵生成完毕" << endl; return Ls; } / * 最小二乘法求解方程 * @param mesh * @param Ls * @param b * @return */ int solve_poison(SurfaceMesh &mesh, const SparseMatrixType &Ls, const Eigen::MatrixXf &b) { Eigen::SparseMatrix<Scalar> ls_transpose = Ls.transpose(); Eigen::SparseMatrix<Scalar> LsLs = ls_transpose * Ls; Eigen::SimplicialCholesky<Eigen::SparseMatrix<Scalar> > MatricsCholesky(LsLs); Eigen::VectorXf xyzRHS = ls_transpose * b; Eigen::VectorXf xyz = MatricsCholesky.solve(xyzRHS); for (auto v : mesh.vertices()) { Point &p = mesh.position(v); p[1] = xyz[v.idx()]; } return 0; } 

线性压缩

求解完成后对整个模型的z坐标线性压缩
$$z_i=\beta \cdot (z_i-z_{min})/(z_{max}-z_{min})\text{\hspace{1em}(9)}$$

讯享网/ * 对z轴线性压缩 * @param mesh * @param beta * @return */ int compression(SurfaceMesh &mesh, Scalar beta) { cout << "正在对z轴线性压缩" << endl; Scalar z_i, z_min = 0x3fffffff, z_max = -0x3fffffff; for (auto v : mesh.vertices()) { Point p = mesh.position(v); if (p[1] > z_max) z_max = p[1]; if (p[1] < z_min) z_min = p[1]; } cout << "z_max = " << z_max << ", z_min = " << z_min << endl; assert(z_min <= z_max); if (z_min < 0) { for (auto v : mesh.vertices()) { Point &p = mesh.position(v); p[1] -= z_min; } z_min = 0; z_max -= z_min; } for (auto v : mesh.vertices()) { Point &p = mesh.position(v); z_i = p[1]; //执行线性压缩，原压缩公式似乎有问题，这里在beta之后加入了z_i p[1] = beta * z_i * (z_i - z_min) / (z_max - z_min); //cout << z_i - p[1] << endl; } cout << "压缩完成" << endl; return 0; } 

结果

Note

在我的实现中，简单将边界约束设置为z=0，在某些情况下可能存在边界上两个点重合的情况，导致最后生成模型在重叠处有一个大凸起，这是由于边界约束和基平面没有一一对应的缘故。

完整代码发布于github：https://github.com/XuRongYan/relief_generation

参考文献

[1] Zhang Y W , Zhou Y Q , Li X L , et al. Bas-Relief Generation and Shape Editing through Gradient-Based Mesh Deformation[J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(3):328-338.

[2] Yu Y , Zhou K , Xu D , et al. Mesh editing with poisson-based gradient field manipulation[J]. ACM Transactions on Graphics, 2004, 23(3):644.

[3] Nealen A, Igarashi T, Sorkine O, et al. Laplacian mesh optimization[C]// International Conference on Computer Graphics & Interactive Techniques in Australasia & Southeast Asia. 2006.