对象的克隆

浅克隆

如果一个类需要支持浅克隆的操作，则需要实现Cloneanle接口【标志接口】，用于告知VM这个类型的对象需要支持克隆操作。如果一个类没有实现接口，当调用clone()方法时则会抛出异常CloneNotSupportException

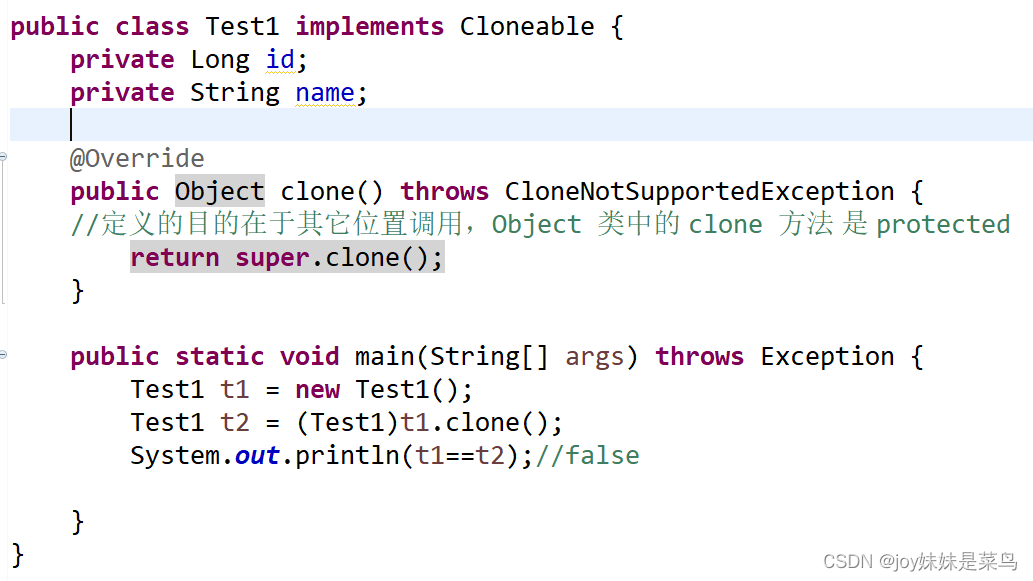
讯享网

深克隆

如果需要深克隆可以使用对象流实现，它会将所有相关的内容进行一次拷贝，针对引用类型属性不会只拷贝地址值。通过对象流实现对象的拷贝，则要求对象所属于的类必须实现Serializable接口

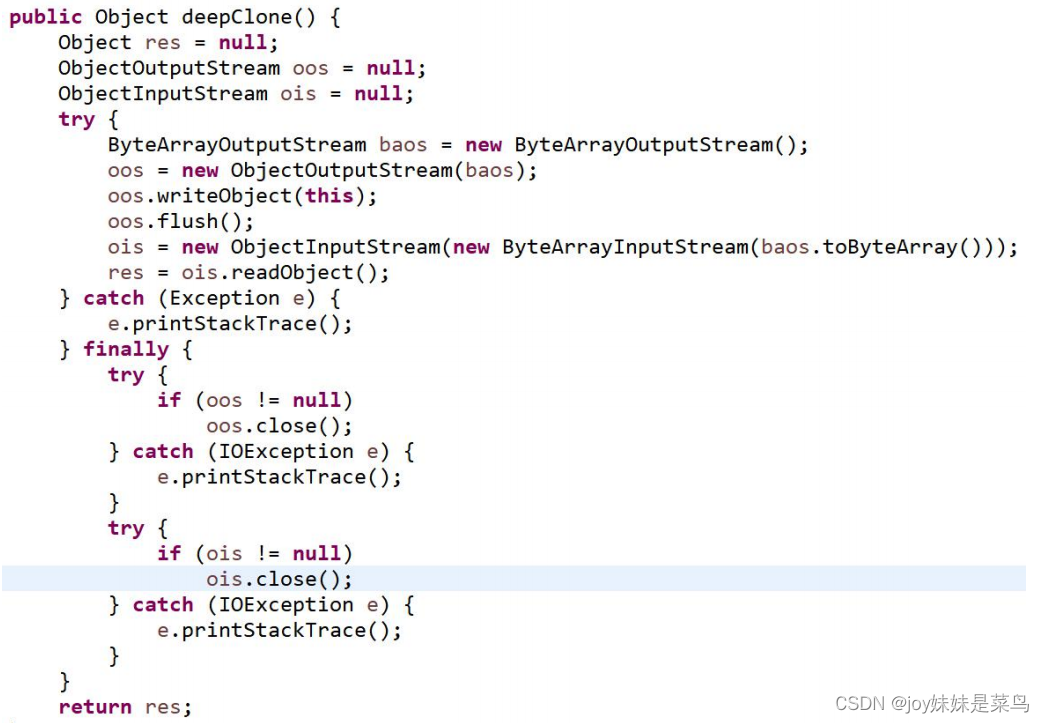
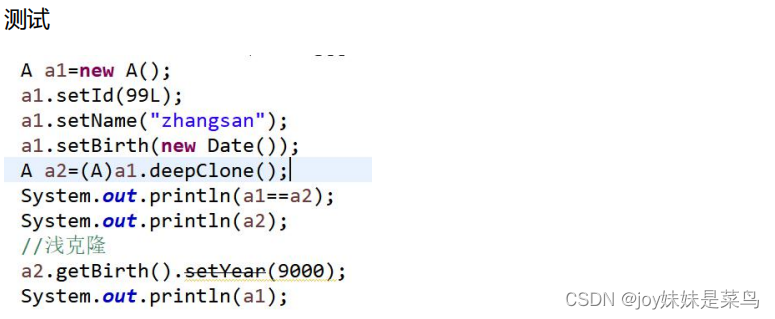
Set接口

扩展自Collection接口

• 顶级接口Collection无序、允许重复
• 子接口List有序、允许重复
• 子接口Set无序、不允许重复

允许存储null值

对add、equals和hashcode方法添加了限制

Set接口的具体实现

HashSet和TreeSet接口的具体实现，还有一个特殊的LinkedHashSet实现类

Set接口–>HashSet实现类–>LinkedHashSet实现类

Set接口–>SortedSet接口–>TreeSet实现类

HashSet的底层实现就是HashMap，初始化后容积(16、0.75)

• 存储数据的要求：首先调用存储对象的hashcode方法获取当前对象的hash值，然后如果hash值相等则出现覆盖
• 哈希表存储数据，具体的存储位置和对象的hash值相关，所以发现存储的数据是无序的
• LinkedHashSet就是在HashSet的基础上，后台维护一个运行于所有条目的链表，用于存储添加元素的顺序

树结构

树实际上就是一种抽象数据类型ADT或者实现这种抽象数据类型的数据结构，可以用于模拟具有树状结构性质的数据集合，是由n个有限节点构成的一个具有层次关系的集合

树的特点

1. 每个节点都只有有限个子节点或者无子节点
2. 没有父节点的节点称为树节点
3. 每个非根节点有且仅有一个父节点
4. 除了根节点外，每个子节点可以分为多个互不相关的子树
5. 树中没有环路cycle

引入树结构目的在于结合有序数组和链表两种数据结构的优点

二叉树

二叉树就是每个节点最多有 2 个分叉子节点，具体的存储方式有基于指针的链式存储和基于数组的顺序存储，最常见的是基于指针的方式，基于数组的方式比较浪费内存

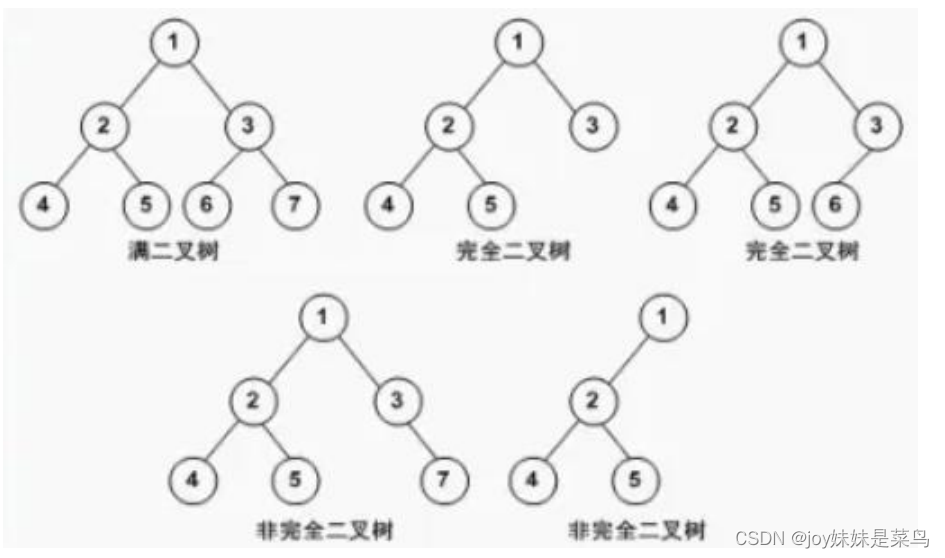
满二叉树：每个节点都有左右两个子节点

完全二叉树：叶子节点分布在层次结构的最下面或者倒数第二层，最下面一层的叶子节点都靠左排列。除了最下

面一层，其他层结点都是饱满的，并且最下层上的结点都集中在该层最左边的若干位置上。（满二叉树也是完全二叉树）

存储方式

• 基于指针的链式存储方式

public class Node{ 
    private int data;//需要存储的数据  private Node left;//左子树  private Node right;//右子树  } 

• 基于数组的链式存储方式

对于节点之间的父子关系，通过数组的下标计算得到对应的存储位置。例如节点 x 存储数组中下标为 i 的位置，

那么下标为 2i 的位置存储的是它的左子节点；下标 2i+1 的位置存储的就是它的右子节点，下标为 i/2 的位置存

储的就是它的父节点

遍历方式

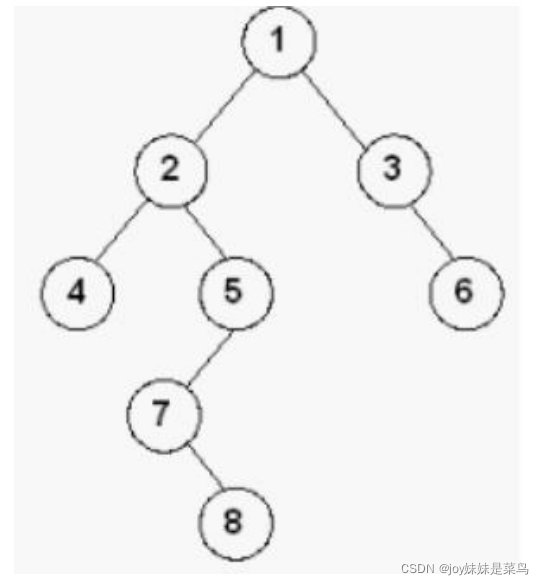
前序遍历

讯享网前序遍历：根--左--右 1,2,4,5,7,8,3,6 public void preOrder(Node root){ 
    if(root==null) return; System.out.println(root.data); preOrder(root.left); preOrder(root.right); } 

中序遍历

中序遍历：左--根--右 4,2,7,8,5,1,3,6 public void middleOrder(Node root){ 
    if(root==null) return; middleOrder(root.left); System.out.println(root.data); middleOrder(root.right); } 

后序遍历

讯享网后序遍历：左--右--根 4,8,7,5,2,6,3,1 public void postOrder(Node root){ 
    if(root==null) return; postOrder(root.left); postOrder(root.right); System.out.println(root.data); } 

排序二叉树

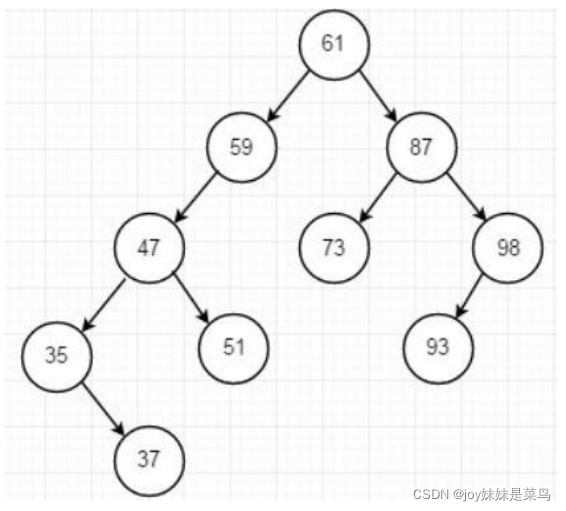
首先如果二叉树满足条件每个节点：左子树的所有节点值都小于它的根节点，而且所有右子树节点值大于它的根节点，这样的二叉树就是排序二叉树

折半查找算法

public class Test1 { 
    public static void main(String[] args) { 
    int[] arr = new int[11]; arr[0] = 300; Random r = new Random(); for (int i = 1; i < arr.length; i++) { 
    arr[i] = r.nextInt(1000); } Arrays.sort(arr); System.out.println(Arrays.toString(arr)); Test1 t1 = new Test1(); int index = t1.halfSearch(arr, 300); System.out.println(index); } public int halfSearch(int[] arr, int target) { 
    int min = 0; int max = arr.length - 1; while (min <= max) { 
    int mid = (min + max) >> 1; if (target > arr[mid]) { 
    min = mid + 1; } else if (target < arr[mid]) { 
    max = mid - 1; } else { 
    return mid; } } return -1; } } 

编码实现

插入数据

首先从根节点开始向下查找自己需要插入数据的具体位置。具体流程:新节点和当前节点进行比较，如果相同则标识已经存在且不能重复插入；如果小于当前节点，则转向到左子树中接续查找，如果左子树为空，则当前节点为要查找的父节点，新节点插入到当前节点的左子树即可。如果大于当前节点，则到右子树中寻找，如果右子树为空则当前节点为要查找的父节点，新节点插入到当前节点的右子树即可。

讯享网 public void insert(int data) { 
    if (tree==null) { 
    tree = new Node(data); return; } Node p = tree; while (p!=null) { 
    if (data>p.data) { 
    if (p.right==null) { 
    p.right = new Node(data); } p = p.right; }else { 
    if (p.left==null) { 
    p.left = new Node(data); } p = p.left; } } } 

删除操作

删除操作有 3 种情况：要删除的节点无子节点、要删除的节点只有一个子节点、要删除的节点有两个子节点

• 要删除的节点无子节点可以直接删除，就是让其父节点将该子节点置空即可
• 要删除的节点只有一个子节点，则替换要删除的节点为其子节点
• 要删除的节点有两个子节点，则首先查找该节点的替换节点（就是右子树中最小的节点或者左子树中的最大节点），接着替换要删除的节点为替换节点，然受删除替换节点

 public void delete(int data) { 
    Node p = tree; Node pp = null; while (p != null && p.data != data) { 
    pp = p; if (data > p.data) p = p.right; else p = p.left; } if (p == null) return; if (p.left != null && p.right != null) { 
    Node minp = p.right; Node minpp = p; while (minp.left != null) { 
    minpp = minp; minp = minp.left; } p.data = minp.data; p = minp; pp = minpp; } Node child = null; if (p.left != null) child = p.left; if (p.right != null) child = p.right; if (pp == null) tree = child; else if (pp.left == p) pp.left = child; else pp.right = child; }