一边学,一边记。
简单相关系数:仅仅研究两个变量之间的关系
偏相关系数:多个相关变量中研究两个变量之间的关系
多元回归:多个不相关(理想化,不存在完全不相关)自变量与一个因变量之间的关系
通径分析:多个相关的自变量与一个因变量之间的关系
典型相关系数:多个相关的因变量与多个相关的自变量之间的关系
看图
讯享网
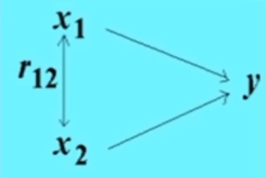
图中箭头表示自变量之间存在因果关系,x1直接指向y为x1对y的直接通径。
r表示变量之间的相关系数
在直接通径上,若xi到的值增加一个标准差单位时,y将要改变的标准差单位Piy,称为通径xi到y的系数。
这里x1与x2相关,所以x1在影响y时,同时也在通过x2影响着y。它通过x2影响y的称为间接通径。

在通径分析中,一般认为最难计算的就是通径系数P,但其实,对数据做线性回归时,得到的标准化系数,就是通径系数。
用SPSS计算很方便,用Python也可以,但是Python要先对所有数据标准化再进行多元回归。得到标准化系数。
比如下面的数据。
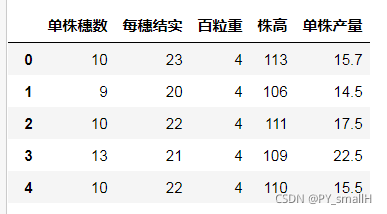
这就15行数据,所有的数据如下:
array([[ 10. , 23. , 4. , 113. , 15.7], [ 9. , 20. , 4. , 106. , 14.5], [ 10. , 22. , 4. , 111. , 17.5], [ 13. , 21. , 4. , 109. , 22.5], [ 10. , 22. , 4. , 110. , 15.5], [ 10. , 23. , 4. , 103. , 16.9], [ 8. , 23. , 3. , 100. , 8.6], [ 10. , 24. , 3. , 114. , 17. ], [ 10. , 20. , 3. , 104. , 13.7], [ 10. , 21. , 3. , 110. , 13.4], [ 10. , 23. , 4. , 104. , 20.3], [ 8. , 21. , 4. , 109. , 10.2], [ 6. , 23. , 3. , 114. , 7.4], [ 8. , 21. , 4. , 113. , 11.6], [ 9. , 22. , 4. , 105. , 12.3]]) 讯享网
用spss做多元线性回归
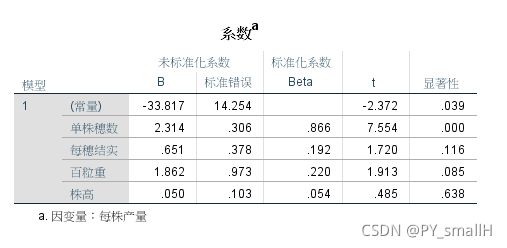
结果中株高的系数不显著,不具有统计学意义,可以先去除掉看一看
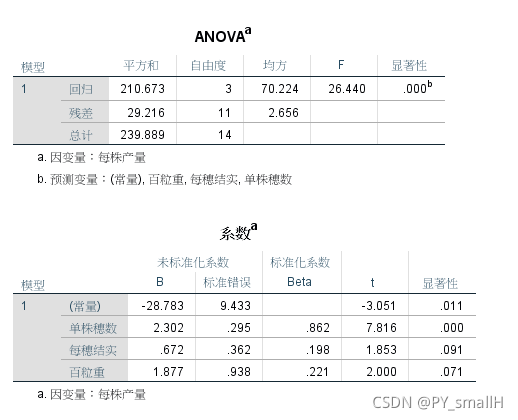
可以看到标准化系数那一列中,就是我们要得到的直接通径P值。
我们再计算一下他的皮尔森相关系数:
讯享网np.corrcoef(df1,rowvar=False)
array([[ 1. , -0., 0., -0.0, 0.], [-0., 1. , -0., 0., 0.0], [ 0., -0., 1. , -0.0, 0.], [-0.0, 0., -0.0, 1. , -0.00], [ 0., 0.0, 0., -0.00, 1. ]]) 这是5X5的矩阵,第一行就表示x1 。
这个矩阵最后一列就就是所有变量对y的影响。

算一下单株穗数,也就是第一个变量,他的直接通径为P = 0.862
总结,从相关系数并不能看出这个变量对y的影响大小,因为变量间也会相关,并且变量间相关度越高,本身自变量对y的单独影响可能就会越低。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/10945.html