1 MAE
- Mean Absolute Error ,平均绝对误差
- 是绝对误差的平均值
for x, y in data_iter: y=model(x) d = np.abs(y - y_pred) mae += d.tolist() #mae=sigma(|pred(x)-y|)/m MAE = np.array(mae).mean()讯享网
MAE/RMSE需要结合真实值的量纲才能判断差异。
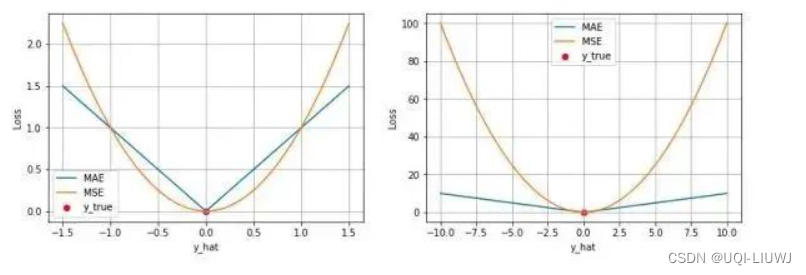
下图是指,假如ground truth是0,那么MAE和prediction之间的关系(后同)
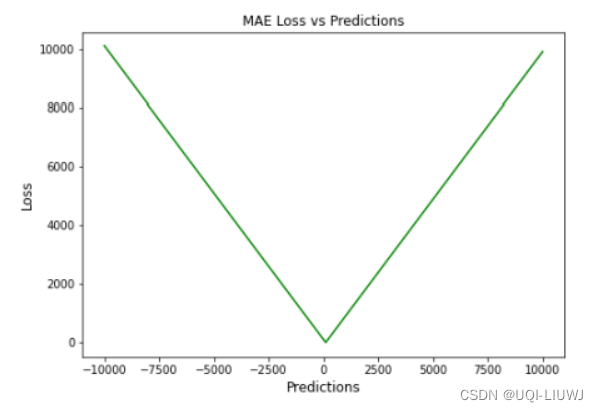
1.1 优缺点
优点:
- 计算简单
- 对异常值不太敏感
缺点:
- 在prediction已经很接近ground-truth的时候,梯度依然很大——>可能在梯度下降的时候跳过最小值
- 在0处不可微
1.2 背后的假设
- 模型预测与真实值之间的误差服从拉普拉斯分布 (μ=0,b=1)
- 给定一个xi模型输出真实值 yi的概率为
- 最大似然:
- 给定一个xi模型输出真实值 yi的概率为
2 RMSE
- Root Mean Square Error,均方根误差
- 是观测值与真值偏差的平方和与观测次数m比值的平方根。
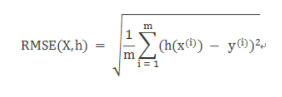
讯享网for x, y in data_iter: y=model(x) d = np.abs(y - y_pred) mse += (d 2).tolist() #mse=sigma((pred(y)-y)^2)/m RMSE = np.sqrt(np.array(mse).mean())
MAE/RMSE需要结合真实值的量纲才能判断差异。
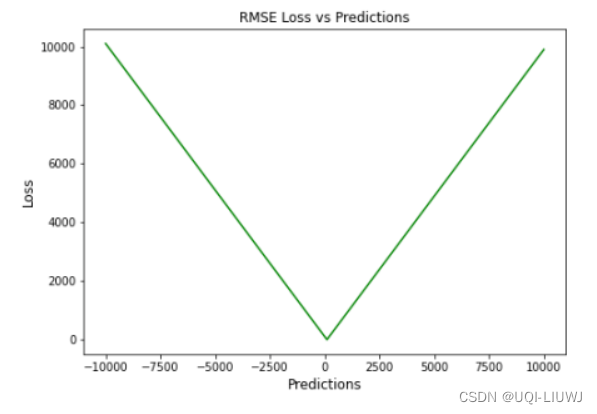
2.1 RMSE与MAE的对比
RMSE相当于L2范数,MAE相当于L1范数。
次数越高,计算结果就越与较大的值有关,而忽略较小的值。
所以这就是为什么RMSE针对异常值更敏感的原因(即有一个预测值与真实值相差很大,那么RMSE就会很大)。
最小化 MAE 的预测方法将导致预测中位数,而最小化 RMSE 将导致预测均值。
相对来说,MAE和MAPE不容易受极端值的影响;而MSE/RMSE采用误差的平方,会放大预测误差,所以对于离群数据更敏感,可以突出影响较大的误差值。
2.2 缺点
- RMSE仍然是一个线性平分函数,所以梯度在最小值附近是突变的
- 随着误差幅度的增加,RMSE 对异常值的敏感性也随之增加
3 SD
- Standard Deviation ,标准差
- 是方差的算数平方根

4 MSE
- Mean Squared Error,均方误差
-

- 当误差被平方时,离群值被赋予更多的权重。受益于这种对离群 Loss 的惩罚,有助于优化算法获得参数的**值
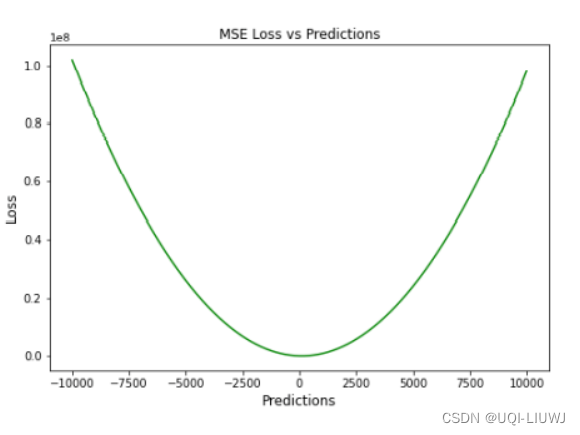
4.1 优缺点
优点:
- 在prediction接近ground-truth的时候,梯度会逐渐减少
- ——>有助于对微小错误进行有效的最小收敛
- 用二次方程表示,有助于在异常值的情况下调整模型参数。
- 离群值被赋予更多的权重
缺点
- 较高的损失值可能会导致反向传播过程中的大幅跳跃
- 对异常值特别敏感,这意味着数据中的显著异常值可能会影响模型性能
4.2 MSE背后的假设
- 假设模型预测与真实值之间的误差服从标准高斯分布N(0,1)
- 则给定一个xi模型输出真实值yi的概率为
-
- 进一步我们假设数据集中 N 个样本点之间相互独立,则给定所有 x输出所有真实值y的概率(似然 Likelihood)
- 取log
- 去点和yi无关的一项,就转化为MSE:
- 则给定一个xi模型输出真实值yi的概率为
4.3 MAE 和 MSE的对比
- MSE 通常比 MAE 可以更快地收敛
- 当使用梯度下降算法时,MSE 损失的梯度为
 ,而 MAE 损失的梯度为±1
,而 MAE 损失的梯度为±1
- 即 MSE 的梯度的 scale 会随误差大小变化,而 MAE 的梯度的 scale 则一直保持为 1
- 即便在绝对误差
 很小的时候 MAE 的梯度 scale 也同样为 1
很小的时候 MAE 的梯度 scale 也同样为 1
- 这实际上是非常不利于模型的训练的。
- 这导致了 MSE 在大部分时候比 MAE 收敛地更快。
- 这个也是 MSE 更为流行的原因。
- 当使用梯度下降算法时,MSE 损失的梯度为
- MAE 对于 outlier 更加 robust
- 由于MAE 损失与绝对误差之间是线性关系,MSE 损失与误差是平方关系,当误差非常大的时候,MSE 损失会远远大于 MAE 损失。
- 因此当数据中出现一个误差非常大的 outlier 时,MSE 会产生一个非常大的损失,对模型的训练会产生较大的影响。

5 MAPE
- Mean Absolute Percentage Error 平均绝对百分比误差
- 范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
- 当真实值有数据等于0时,存在分母0除问题,该公式不可用!
How to calculate MAPE with actual values at or close to 0 (stephenallwright.com)
for x, y in data_iter: y=model(x) d = np.abs(y - y_pred) mape += (d / y).tolist() #mape=sigma(|(pred(x)-y)/y|)/m MAPE = np.array(mape).mean()
5.1 优点
- 百分比误差具有无单位的优势,因此经常用于比较数据集之间的预测性能。
- 利用了绝对百分比误差,避免了正数抵消负数的问题
5.2 缺点
基于百分比误差的度量的缺点是,如果 对于评估的时间片期间的任何 t,yt=0 。则这一个PE为无穷大,如果任何 yt 接近于零,则具有极端值。
6 SMAPE
- Symmetric Mean Absolute Percentage Error 对称平均绝对百分比误差

- 当真实值有数据等于0,而预测值也等于0时,存在分母0除问题,该公式不可用!
7 sklearn实现
sklearn 笔记整理:sklearn.mertics_UQI-LIUWJ的博客-CSDN博客
8 scaled error
在比较具有不同单位的时间序列的预测准确性时,提出了比例误差scaled error作为PE percentage error的替代方法。

- 对于非季节性时间序列,一种有用的方法是定义一个naive的预测方法,来计算比例误差
因为分子和分母都涉及原始数据尺度上的值,所以 qj 与数据尺度无关。
如果一个比例误差是由 比naive预测更好的预测产生的,则qj小于 1。
相反,如果预测比naive预测更差,则qj大于 1。
- 对于季节性数据,我们可以:使用一个季节性naive预测方法,来达到同样的效果:

8.1 MASE mean absolute scaled error
参考内容:2211.02989.pdf (arxiv.org)
A Comprehensive Survey of Regression Based Loss Functions for Time Series Forecasting
9 MBE mean bias error
- 平均偏差误差 (MBE)
- 正偏差表示数据误差被高估,而负偏差表示误差被低估

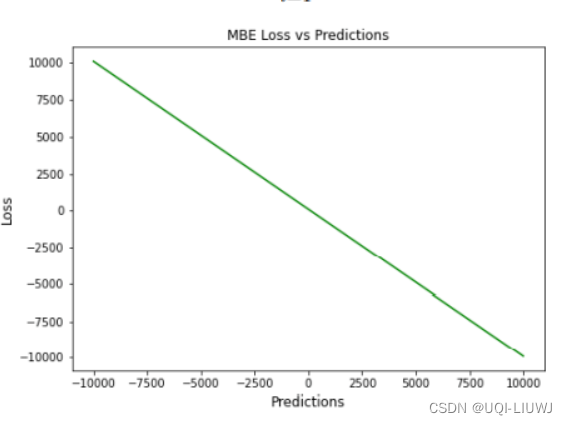
9.1 优缺点
优点
- 确定模型误差的方向
缺点
- 误差往往会相互抵消,不是一个合适的损失函数
- 对于(-∞,+∞)的数字,不是一个合适的损失函数
10 RAE
将总绝对误差除以平均值与实际值之间的绝对差值
 ,其中
,其中
接近零代表模型良好。

10.1 缺点
如果预测值等于真实值,那么RAE将变得不可预测
11 RSE
 ,其中
,其中

12 Mean Squared Logarithmic Error (MSLE)
- 添加对数减少了 MSLE 对实际值和预测值之间的百分比差异以及两者之间的相对差异的关注
- MSLE 将粗略地处理小的实际值和预期值之间的微小差异以及大的真实值和预测值之间的巨大差异
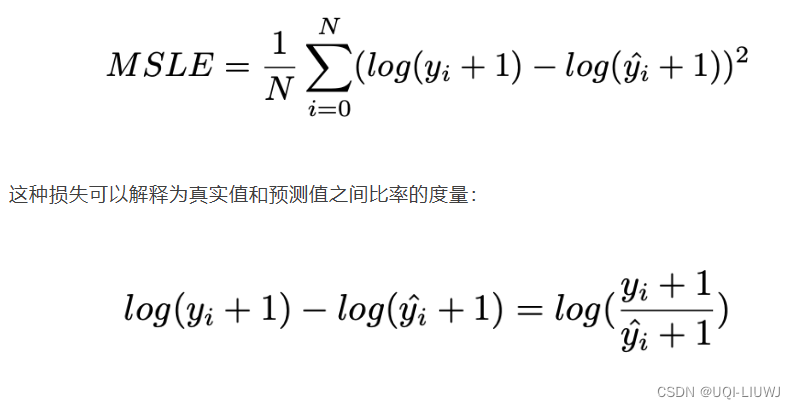
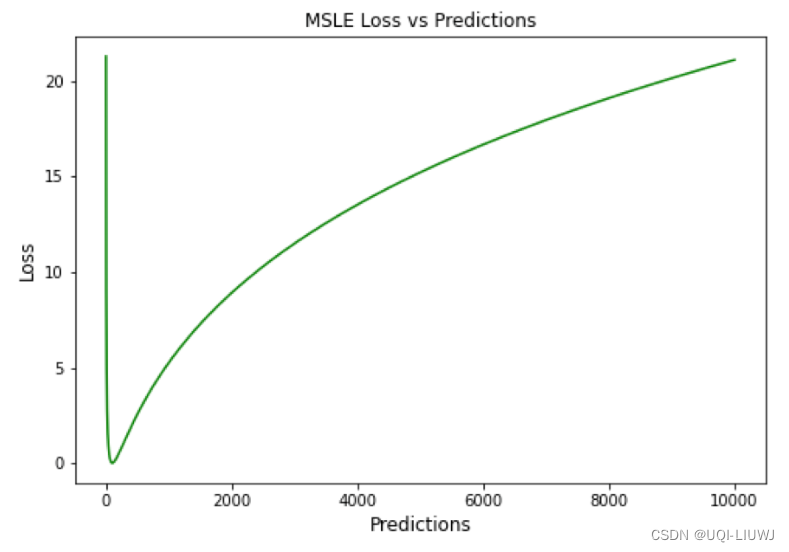
12.1 缺点
- 惩罚不充分的预测,比惩罚过度的预测更多
- 如上图所示,0左边斜率远大于0右边的斜率
13 RMSLE
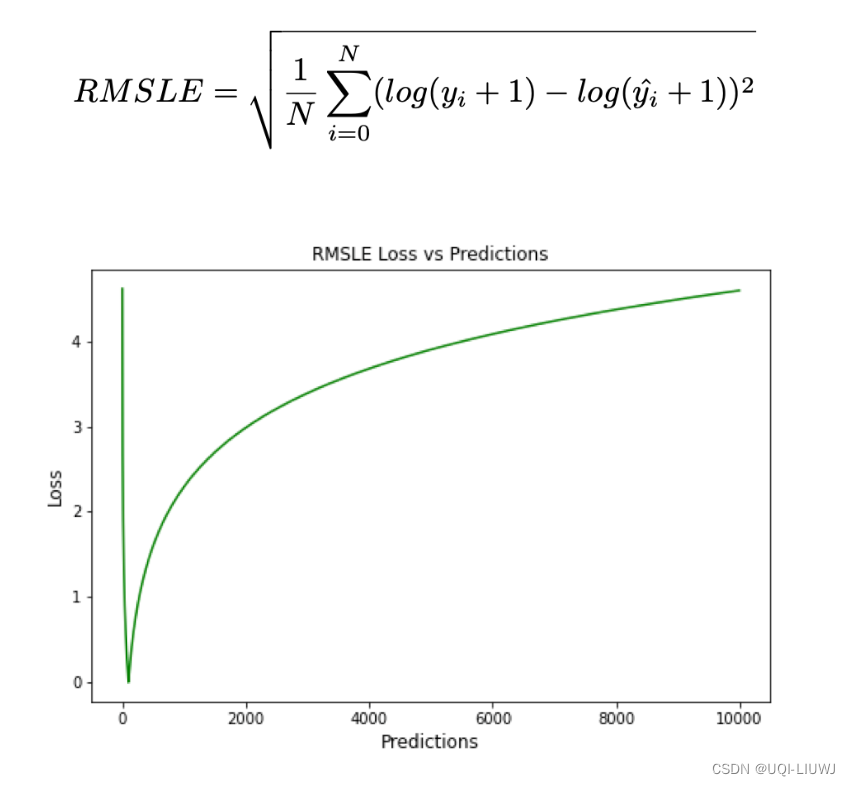
13.1 缺点
同样地,低估比高估会受到更严重的惩罚
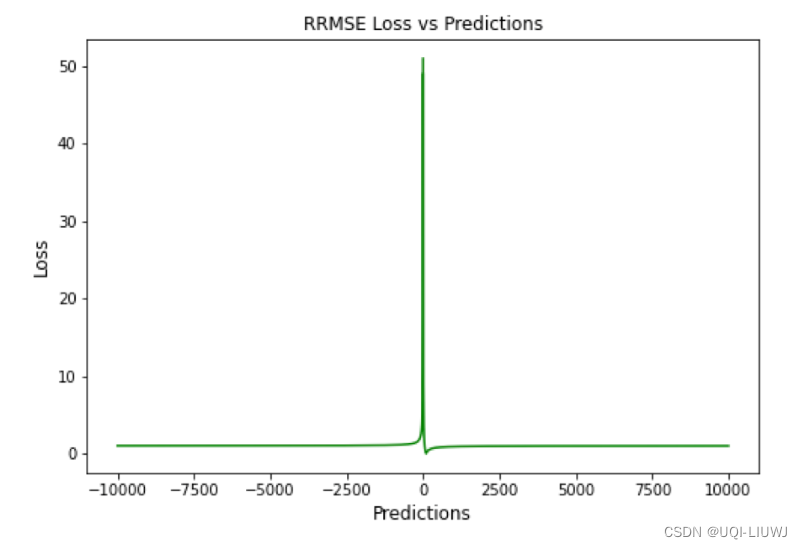
14 RRMSE
- Relative Root Mean Squared Error (RRMSE)
- RRMSE 是没有维度的 RMSE 变体。
- 相对均方根误差(RRMSE)是一种均方根误差度量,它已根据实际值进行缩放,然后由均方根值归一化。
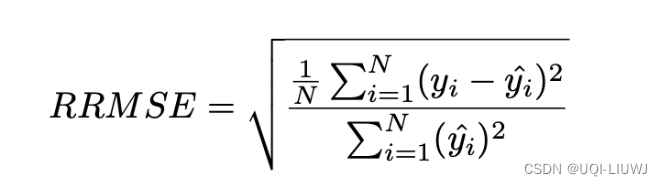
15 Huber Loss
- 二次和线性评分算法的理想组合
- 对于小于 delta 的损失值,应该使用 MSE
- 对于大于 delta 的损失值,应使用 MAE。
- 这成功地结合了两种损失函数的最大特点。
 15.1 优点
15.1 优点
- 超参数δ以外的线性保证了异常值被赋予适当的权重
- 超参数δ以内的弯曲性保证了在反向传播过程中梯度长度合理
15.2 缺点
- 需要额外的条件和比较,在计算上非常昂贵
- 不太适用数据集特别大的情况
16 LogCosh Loss

16.1 优势
- 类似于Huber Loss,也是线性+二次曲线
- 相比于Huber Loss,所需计算更少
16.2 缺点
- 适应性不如Huber Loss(没有δ超参数)
- 推导比Huber更复杂

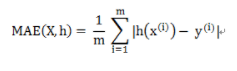
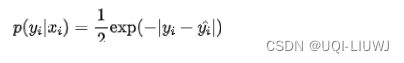


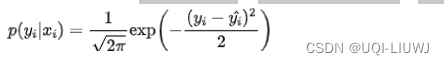
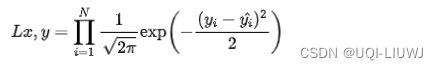

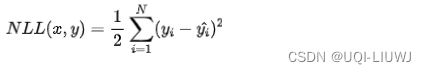





 15.1 优点
15.1 优点
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/103468.html