Flexible Aggregate Nearest Neighbor Queries in Road Networks 论文概述
本文的讨论基于论文
Flexible Aggregate Nearest Neighbor Queries in Road Networks
Published in: 2018 IEEE 34th International Conference on Data Engineering (ICDE)
论文链接:https://ieeexplore.ieee.org/document/
本文解决了哪些问题
\uad 集合最近邻查询 ( A N N ) (ANN) (ANN)问题在欧氏空间和道路网络等领域一直是一个热门的研究方向。灵活的集合最近邻查询 ( F A N N ) (FANN) (FANN)问题通过引入一个灵活性来扩展了 A N N ANN ANN问题。 F A N N FANN FANN问题简略定义为,给定一个数据点集合P,一个查询点集合Q,一个用户自定义的范围在(0,1]之间的灵活性参数 ψ \psi ψ , F A N N FANN FANN算法能返回P中到Q中任意 ψ ∣ Q ∣ \psi |Q| ψ∣Q∣个点总距离最小的那个点。在这篇文章中,作者专注于解决与道路网络相关的问题( F A N N R FANN_R FANNR),并展示了一系列用于解决 F A N N R FANN_R FANNR问题的算法;这些算法包括$Dijkstra-based 方 法 , 方法, 方法,queue-based 方 法 , 组 合 方法,组合 方法,组合IER 和 和 和kNN 两 种 思 想 的 算 法 。 同 时 作 者 也 提 出 了 一 些 针 对 两种思想的算法。同时作者也提出了一些针对 两种思想的算法。同时作者也提出了一些针对max-FANN_R$ 问题特定的算法,以及对 s u m − F A N N R sum-FANN_R sum−FANNR 问题的近似算法。这些特定的算法非常容易实现,并且在解决某些问题中性能十分优越。
基本算法的描述
A . D i j k s t r a − b a s e d   A l g o r i t h o m I n p u t :   G ( V , E , W ) , Q , ψ O u t p u t :   p ∗ , Q ψ ∗ , d ∗ 1 : p ∗ ← n u l l , Q ψ ∗ ← ⊘ , d ∗ ← ∞ 2 : f o r   e a c h   p ∈ V d o 3 : 用 D i j k s t r a 算 法 找 到 Q 中 距 离 p 最 近 的 [ ψ M ] 个 点 Q ψ P , 同 时 求 出 它 们 到 p 的 距 离 之 和 d 4 : i f   d < d ∗ t h e n 5 : p ∗ ← p , Q ψ ∗ ← Q ψ P , d ∗ ← d 6 : e n d    i f 7 : e n d f o r A.\quad Dijkstra-based\, Algorithom\\ Input:\,G(V,E,W),Q,\psi \\ Output:\,p^*,Q_\psi^*,d^* \uad\quad\\ 1:p^*\leftarrow null,Q_\psi^*\leftarrow\oslash,d^*\leftarrow \infty\\ 2:for\, each\,p\in V\quad do\uad\uad\\ 3:用Dijkstra算法找到Q中距离\quad\\ p最近的[\psi M]个点Q_\psi^P,同时求出它们\\ 到p的距离之和d\uad\uad\uad\uad\\ 4:\uad if\,d<d^*\quad then\uad\quad\\ 5:\uad\uad p^*\leftarrow p,Q_\psi^*\leftarrow Q_\psi^P, \\\uad d^*\leftarrow d\\ 6:\quad end\;if\uad\uad\uad\uad\\ 7:endfor\uad\uad\uad\uad A.Dijkstra−basedAlgorithomInput:G(V,E,W),Q,ψOutput:p∗,Qψ∗,d∗1:p∗←null,Qψ∗←⊘,d∗←∞2:foreachp∈Vdo3:用Dijkstra算法找到Q中距离p最近的[ψM]个点QψP,同时求出它们到p的距离之和d4:ifd<d∗then5:p∗←p,Qψ∗←QψP,d∗←d6:endif7:endfor
B . I E R − k N N   F r a m e w o r k Input: G , P , Q , ψ , g , R Output: p ∗ , Q ψ ∗ , d ∗ 1 : d ∗ ← ∞ , H ← 新 优 先 队 列 2 : H . e n q u e u e ( R . r o o t , g ψ ϵ ( R . r o o t , Q ) )    3 : while   H   i s   n o t   e m p t y   then 4 : e ← H . t o p ( ) 5 : if   g ψ ϵ ( e , Q ) ≥ d ∗ then    6 : break    7 : H . d e q u e u e ( )    8 : if   e   i s   a n   R − T r e e   n o d e   then    9 : foreach   R − T r e e   e n t r y   e ^ o f   e   do 10 : H . e n q u e u e ( e ^ , g ψ ϵ , Q ) 11 : else 12 : ( Q ψ e , d e ) ← g ψ ( e , Q ) 13 : if d e < d ∗   then 14 : p ∗ ← e , d ∗ ← d e , Q ψ ∗ ← Q ψ e B.IER-kNN\,Framework\uad\uad\quad\\ \textbf{Input:}G,P,Q,\psi,g,R\uad\quad\uad\uad\\ \textbf{Output:}p^*,Q_\psi^*,d^*\uad\uad\quad\uad\uad\\ 1:d*\leftarrow \infty,H\leftarrow 新优先队列\uad\quad\uad\\ 2:H.enqueue(R.root,g_\psi^\epsilon(R.root,Q))\,\,\\ 3:\textbf{while}\,H\,is \,not\,empty\,\textbf{then}\uad\uad\\ 4:\quad e\leftarrow H.top()\uad\uad\uad\uad\quad\\ 5:\quad\textbf{if}\,g_\psi^\epsilon(e,Q)\ge d^* \textbf{then}\uad\uad \quad\,\,\\ 6:\uad\textbf{break}\uad\uad\uad\uad\uad\,\,\\ 7:\quad H.dequeue()\uad\uad\uad\uad\,\,\\ 8:\quad\textbf{if}\, e\,is\,an\, R-Tree\, node\, \textbf{then}\quad\,\,\\ 9:\quad\textbf{foreach}\,R-Tree\,entry\,\hat e of\,e\,\textbf{do}\\ 10:\uad H.enqueue(\hat e,g_\psi^\epsilon,Q)\uad\uad\\ 11:\quad\textbf{else}\uad\uad\uad\uad\uad\uad\\ 12:\uad(Q_\psi^e,d^e)\leftarrow g_\psi(e,Q)\uad\uad\\ 13:\uad\textbf{if}\quad d^e<d^*\,\textbf{then}\uad\uad\quad\\ 14:p^*\leftarrow e,d^*\leftarrow d^e,Q_\psi^*\leftarrow Q_\psi^e\uad\quad B.IER−kNNFrameworkInput:G,P,Q,ψ,g,ROutput:p∗,Qψ∗,d∗1:d∗←∞,H←新优先队列2:H.enqueue(R.root,gψϵ(R.root,Q))3:whileHisnotemptythen4:e←H.top()5:ifgψϵ(e,Q)≥d∗then6:break7:H.dequeue()8:ifeisanR−Treenodethen9:foreachR−Treeentrye^ofedo10:H.enqueue(e^,gψϵ,Q)11:else12:(Qψe,de)←gψ(e,Q)13:ifde<d∗then14:p∗←e,d∗←de,Qψ∗←Qψe
C . T h e   E x a c t − m a x   A l g o r i t h m I n p u t : G , P , Q , ψ , δ , g O u t p u t : p ∗ , Q ψ ∗ , d ∗ 1 : for each   p ∗ ∈ P   d o 2 : c o u n t [ p ] ← 0     3 : while   t r u e d o    4 : L m i n ← 头 节 点 距 离 的 最 小 队 列 5 : c o u n t [ L m i n . t o p ( ) ] ← c o u n t [ L m i n . t o p ( ) ] + 1 6 : if    c o u n t [ L m i n . t o p ( ) ] ≥ ψ ∣ Q ∣ then 7 : p ∗ ← L m i n . t o p ( ) ( Q ψ ∗ , d ∗ ) ← g ψ ( L m i n . t o p ( ) , Q ) 8 : break 9 : L m i n . d e q u e u e ( ) C.\quad The \,Exact-max\,Algorithm\\ Input:G,P,Q,\psi,\delta,g \uad\uad\quad\\ Output:p^*,Q_\psi^*,d*\uad\uad\uad\\ 1:\textbf{for each}\,p^*\in P\,do\uad\uad\quad\\ 2:\quad count[p]\leftarrow 0\uad\uad\quad\quad\,\,\,\\ 3:\textbf{while}\, true \quad do\uad\uad\uad\,\,\\ 4:\quad L_{min}\leftarrow 头节点距离的最小队列\\ 5:\quad count[L_{min}.top()]\leftarrow \uad\quad\\ count[L_{min}.top()]+1\\ 6:\quad\textbf{if}\;count[L_{min}.top()]\ge \psi|Q|\\ \textbf {then}\quad\uad\uad\uad\quad\\ 7:\uad \uad p*\leftarrow L_{min}.top()\uad\\ (Q_\psi^*,d^*)\leftarrow g_\psi (L_{min}.top(),Q)\\ 8:\uad\uad \textbf{break}\uad\uad\uad\\ 9:\quad L_{min}.dequeue()\quad\uad\uad C.TheExact−maxAlgorithmInput:G,P,Q,ψ,δ,gOutput:p∗,Qψ∗,d∗1:for eachp∗∈Pdo2:count[p]←03:whiletruedo4:Lmin←头节点距离的最小队列5:count[Lmin.top()]←count[Lmin.top()]+16:ifcount[Lmin.top()]≥ψ∣Q∣then7:p∗←Lmin.top()(Qψ∗,d∗)←gψ(Lmin.top(),Q)8:break9:Lmin.dequeue()
D . T h e   A P X − s u m   A l g o r i t h m I n p u t : G , P , Q , ψ , δ , g O u t p u t : p α , Q ψ α , d α 1 : c a n d i d a t e ← ⊘ 2 : foreach q ∈ Q   do    3 : p ← t h e   n e a r e s t   n e i g h b o r   o f   q   i n   P 4 : c a n d i d a t e . i n s e r t ( p ) 5 : F A N N R ( G , c a n d i d a t e , Q , ψ , s u m ) D.\quad The\,APX-sum\,Algorithm\uad\quad\\ Input:G,P,Q,\psi,\delta,g\uad\uad\uad\uad\\ Output:p^\alpha,Q_\psi^\alpha,d^\alpha\uad\uad\uad\uad\quad\\ 1:candidate\leftarrow\oslash\uad\uad\uad\uad\quad\\ 2:\textbf{foreach}\quad q\in Q \,\textbf{do}\uad\uad\uad\quad\,\,\\ 3:\quad p\leftarrow the\,nearest\,neighbor\,of\, q\,in\,P\\ 4:\quad candidate.insert(p)\uad\uad\uad\\ 5:FANN_R(G,candidate,Q,\psi,sum)\quad D.TheAPX−sumAlgorithmInput:G,P,Q,ψ,δ,gOutput:pα,Qψα,dα1:candidate←⊘2:foreachq∈Qdo3:p←thenearestneighborofqinP4:candidate.insert(p)5:FANNR(G,candidate,Q,ψ,sum)
举例说明
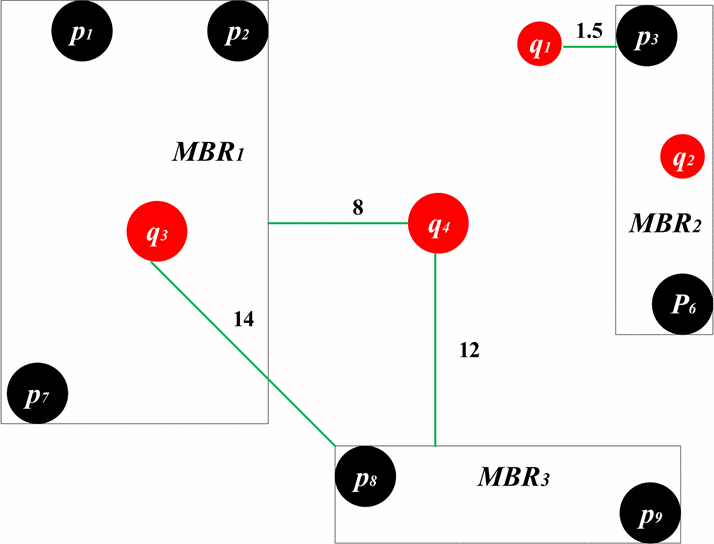
- I E R − k N N F r a m e w o r k IER-kNN\quad Framework IER−kNNFramework 算法
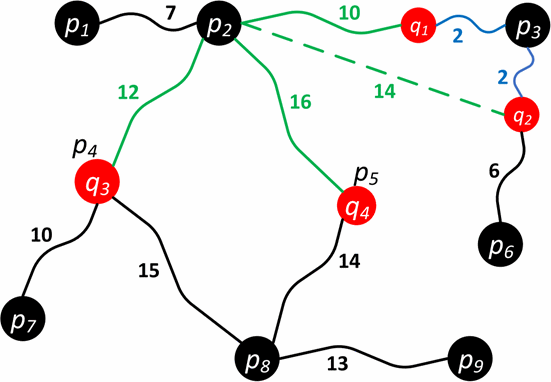
\uad 我们首先看下这个算法是怎么找到 s u m − F A N N R sum-FANN_R sum−FANNR.如图一所示,此时令 ψ = 50 % \psi=50\% ψ=50%.我们在图2中说明这个算法的过程,为了更好地观察这个过程,图中去掉了一些无关的路段。在第一轮的循环中,我们让 ( M B R 1 , 8 ) , ( M B R 2 , 1.5 ) , ( M B R 3 , 26 ) (MBR_1,8),(MBR_2,1.5),(MBR_3,26) (MBR1,8),(MBR2,1.5),(MBR3,26)进入队列H。在这之后, ( M B R 2 , 1.5 ) (MBR_2,1.5) (MBR2,1.5)将会出队,然后我们检查下在 M B R 2 MBR_2 MBR2中的 p 3 , p 6 p_3,p_6 p3,p6。显然, d ∗ d^* d∗将会是4。我们总是能安全的使这个算法停止,这是因为 d ∗ d^* d∗小于队列H中头节点的值。
- E x a c t − m a x Exact-max Exact−max算法
\uad 我们看下这个算法怎么在图一中找到 m a x − F A N N R max-FANN_R max−FANNR,此时 ψ = 50 % \psi=50\% ψ=50%. { q 1 , q 2 , q 3 , q 4 } \{q_1,q_2,q_3,q_4\} { q1,q2,q3,q4}的扩张路径可以用 { p 3 , …   } , { p 3 , …   } , { p 4 , …   } , { p 5 , …   } \{p_3,\dots\},\{p_3,\dots\},\{p_4,\dots\},\{p_5,\dots\} { p3,…},{ p3,…},{ p4,…},{ p5,…}象征性地表示。很明显 p 3 p_3 p3的计数器首先到达 ψ × 4 = 2 \psi \times 4 = 2 ψ×4=2。因此这个 m a x − F A N N R max-FANN_R max−FANNR查询的结果是 p ∗ = p 3 , d ∗ = 2 , Q ψ ∗ = { q 1 , q 2 } p^* = p_3,d^* = 2, Q_\psi^* = \{q_1,q_2\} p∗=p3,d∗=2,Qψ∗={ q1,q2}
- A P X − s u m APX-sum APX−sum算法
\uad 我们仍然通过图一的例子来说明这个算法,此时 ψ = 50 % \psi=50\% ψ=50%。首先,我们可以很容易获得参与的数据点的集合为 A = { p 3 , p 4 , p 5 } A=\{p_3,p_4,p_5\} A={ p3,p4,p5}。因为真正的优化解 p ∗ p^* p∗属于这个集合A,APX-sum将会返回最终结果$p^=p_3, d^ = 4,Q_\psi^*={q_1,q_2} $
采用什么思想解决这个问题
A. T h e D i j k s t r a − b a s e d A l g o r i t h m The\quad Dijkstra-based\quad Algorithm TheDijkstra−basedAlgorithm

\uad 基于 D i j k s t r a Dijkstra Dijkstra的算法基于以下思想。 关于 D i j k s t r a Dijkstra Dijkstra算法运行步骤:在其扩展的每一步,它选择一个未访问的源节点最近节点来访问并更新其邻居到源节点的距离。 这种行为在运行 g ψ ( p , Q ) g_{\psi}(p,Q) gψ(p,Q)时也有意义。 首先,让 p p p为源节点,我们在其上调用 D i j k s t r a Dijkstra Dijkstra算法。 然后我们保持路径扩展直到 ψ ∣ Q ∣ \psi | Q | ψ∣Q∣ 在 Q Q Q中的节点标记为已访问。 因此,这些 ψ ∣ Q ∣ \psi | Q | ψ∣Q∣ 节点恰好是 Q ψ p Q_\psi^p Qψp。因此,我们可以枚举 P P P中的点并返回具有最小柔性聚合距离的点。
B. I E R − k N N F r a m e w o r k IER-kNN\quad Framework IER−kNNFramework
\uad 基于引理1,我们可以使用基于P构建的R树来解决 F A N N R FANN_R FANNR查询。我们在算法 I E R − k N N F r a m e w o r k IER-kNN\quad Framework IER−kNNFramework中展示了这个过程。假设 h e a d head head是一个从队列中获取 h e a d head head元素的函数。最初, R R R树的根被排入优先级队列,该优先级队列按照升序排序 g ψ ϵ ( e , Q ) g_{\psi}^{\epsilon}(e,Q) gψϵ(e,Q)(第2行)。 对于每次迭代,我们首先检查 g ψ ϵ ( e , Q ) g_{\psi}^{\epsilon}(e,Q) gψϵ(e,Q)是否大于或等于当前**候选结果(第5行)。 如果是这样,我们终止算法(第6行); 否则,我们检查出列项是否是R树节点(第8行)。如果是,将此节点下的所有条目推入优先级队列(第9-10行);否则,我们在其上运行 g ψ ϵ ( e , Q ) g_{\psi}^{\epsilon}(e,Q) gψϵ(e,Q)并在 d e < d ∗ d^e<d^* de<d∗时更新结果(第12-14行)。另外,在第9行中,如果 e e e是叶节点,则条目 e e e是 P P P中的数据点,如果 e e e是非叶节点,则它是 R R R树节点。
C.$ The\quad Exact-max\quad Algorithm$
\uad 算法2中提出了 E x a c t − m a x Exact-max Exact−max方法(精确 m a x − F A N N R max-FANNR max−FANNR),它与 R − L i s t R-List R−List具有相似的思想和数据结构。主要区别在于我们为P中的每个点添加一个计数器。最初,这些计数器设置为0(第2行)。在每次迭代期间,我们得到具有最小距离的头节点(第4行),然后将与头节点相关联的计数器增加1(第5行)。如果与头节点相关联的计数器达到$ \psi|Q | , 则 头 节 点 正 好 是 ,则头节点正好是 ,则头节点正好是p^* , 然 后 我 们 可 以 安 全 地 终 止 算 法 ( 第 6 − 9 行 ) 。 因 此 , 我 们 能 运 行 一 次 并 耗 时 ,然后我们可以安全地终止算法(第6-9行)。因此,我们能运行一次并耗时 ,然后我们可以安全地终止算法(第6−9行)。因此,我们能运行一次并耗时g_\psi ( 第 8 行 ) 。 这 就 是 (第8行)。这就是 (第8行)。这就是Exact-max 可 以 高 效 的 原 因 。 此 外 , 这 也 表 明 可以高效的原因。此外,这也表明 可以高效的原因。此外,这也表明g_\psi 的 不 同 实 现 对 的不同实现对 的不同实现对Exact-max 几 乎 没 有 影 响 。 换 句 话 说 , 即 使 我 们 没 有 在 整 个 几乎没有影响。换句话说,即使我们没有在整个 几乎没有影响。换句话说,即使我们没有在整个G$上建立道路网络索引,我们也可获得良好的结果。
D. T h e A P X − s u m A l g o r i t h m The\quad APX-sum\quad Algorithm TheAPX−sumAlgorithm
\uad 对于道路网络中的 s u m − F A N N R sum-FANNR sum−FANNR问题,算法3中提出了近似方法 A P X − s u m APX-sum APX−sum(近似 s u m − F A N N R sum-FANN_R sum−FANNR)。该算法非常简单,但它具有恒定的近似比。我们只检查 Q Q Q中那些查询节点的最近邻居的那些数据点而不是考虑整个 P P P(第2-4行)。 然后我们将候选集视为 P P P,并运行 F A N N R FANN_R FANNR算法(其 g g g为 s u m sum sum)。因此,算法将候选数据点的数量减少到 ∣ Q ∣ | Q | ∣Q∣,通常远小于 ∣ P ∣ | P | ∣P∣。 这就是它可以显着提高搜索效率的原因。 实际上,候选集的大小甚至可能小于 ∣ Q ∣ | Q | ∣Q∣,因为不同的查询点可能具有相同的最近数据点邻居。 A P X − s u m APX-sum APX−sum最吸引人的特性之一是改变 P P P时的稳定性,因为它通常只受 Q Q Q的影响。可以证明该算法的近似比 d α / d ∗ d^\alpha / d^* dα/d∗不大于3。
算法分析的结论
A.$ The \quad Dijkstra-based \quad Algorithm$
\uad 由于 g ψ g_\psi gψ与 D i j k s t r a Dijkstra Dijkstra具有相同的时间成本,即 O ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) O(| E | + | V | log | V |) O(∣E∣+∣V∣log∣V∣)(假设 m i n − p r i o r i t y min-priority min−priority队列由 F i b o n a c c i Fibonacci Fibonacci堆实现),因此总的时间成本是 O ( ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) ∣ P ∣ ) O((| E | + | V | log | V |)| P |) O((∣E∣+∣V∣log∣V∣)∣P∣)。 在最坏的情况下,空间成本是 O ( ∣ P ∣ + ∣ Q ∣ + ∣ V ∣ + 2 ψ ∣ Q ∣ ) = O ( ∣ V ∣ ) O(| P | + | Q | + | V | +2\psi | Q |)= O(| V |) O(∣P∣+∣Q∣+∣V∣+2ψ∣Q∣)=O(∣V∣)。
B. I E R − k N N F r a m e w o r k IER-kNN\quad Framework IER−kNNFramework
\uad 在最坏的情况下,我们仍然需要访问P中的每个点。以 I E R − G T r e e IER-GTree IER−GTree为例, k N N kNN kNN搜索的最差时间成本是 O ( ∣ V ∣ l o g ∣ V ∣ ) O(| V | log | V |) O(∣V∣log∣V∣)。总时间成本为 O ( ∣ P ∣ ∣ V ∣ l o g ∣ V ∣ ) O(| P || V | log | V |) O(∣P∣∣V∣log∣V∣)。 如所述,复杂性比实际中最坏的情况复杂性要小得多。 因为与 G G G树相比, R R R树或 O c c Occ Occ的空间成本可以忽略不计,所以空间成本主要由 G G G树的成本组成,即 O ( ∣ V ∣ + ∣ V ∣ ∣ l o g ∣ V ∣ + ∣ E ∣ ) O(| V | + | V | | log | V | + | E |) O(∣V∣+∣V∣∣log∣V∣+∣E∣)。
C. T h e E x a c t − m a x A l g o r i t h m The\quad Exact-max \quad Algorithm TheExact−maxAlgorithm
\uad 假设 g p s i g_psi gpsi由类似 D i j k s t r a Dijkstra Dijkstra的方法实现。 对于 R − L i s t R-List R−List算法,在最坏的情况下将访问 P P P中的每个点。因此,时间成本是 O ( ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) ∣ P ∣ ) O((| E | + | V | log | V |)| P |) O((∣E∣+∣V∣log∣V∣)∣P∣)。 在实践中,由于下限,时间复杂度通常小于它。 在最坏的情况下,空间成本是 O ( ∣ Q ∣ ∣ V ∣ ) O(| Q || V |) O(∣Q∣∣V∣),它主要由队列列表组成。同样, E x a c t − m a x Exact-max Exact−max的时间成本为 O ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) O(| E | + | V | log | V |) O(∣E∣+∣V∣log∣V∣),其空间成本也包括计数器用量,即 O ( ∣ Q ∣ ∣ V ∣ + ∣ P ∣ ) O(| Q || V | + | P |) O(∣Q∣∣V∣+∣P∣) 在最坏的情况下 = O ( ∣ Q ∣ ∣ V ∣ ) = O(| Q || V |) =O(∣Q∣∣V∣)。
D.$ The APX-sum Algorithm$
A P X − s u m \uad APX-sum APX−sum包括找到最近邻居和 F A N N R FANN_R FANNR。如果 g ψ g_\psi gψ实现为 D i j k s t r a Dijkstra Dijkstra或 I N E INE INE,则时间成本为 O ( ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) ∣ Q ∣ ) O((| E | + | V | log | V |)| Q |) O((∣E∣+∣V∣log∣V∣)∣Q∣)。
在最坏的情况下,空间成本是 O ( ∣ V ∣ ) O(| V |) O(∣V∣)。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/63916.html