人工神经网络

大家好，我是讯享网，很高兴认识大家。

1.基本概念

介绍： 人工神经网络是对人类大脑进行抽象模型化，建立起的一种按不同方式连接起来的网络。在工程与学术界常称其为神经网络（NN）。

人类大脑模型： 人类大脑是由上亿个神经元组成，每个神经元之间由突触连接。当一个神经元受到某种刺激（由上一个突触传递），并且达到一定值（阈值），就会发出某种信号，通过突触传递给下一个神经元。

神经网络运算模型： 神经网络模型包括了多个输入（类似突触），这些输入需要和各自对应的不同权值相乘（收到的信号强弱不同），然后通过一个数学函数来判断是否达到阈值（此函数称为激励函数或激活函数），是否会传递到下一个节点（神经元）。

2.应用范围

人工神经网络在模式识别、智能机器人、自动控制、预测估计、生物、医学和经济等领域应用广泛。

3.对权值的理解与解释

权值指某一因素或某一条件对该事物的影响程度大小。与一般比重不同，权值不仅表示某一因素所占的百分比，更表示其因素的相对重要程度。
性质：
（1）权值越大表示对输入的信号影响越大
（2）权值可以为负值，表示输入信号受到抑制
（3）权值可以被调整，权值调整的过程称为“学习”或“训练”
（4）通过权值调整可以得到固定输入下需要的输出值

4.激活函数的理解与解释

激活函数又称非线性映射，顾名思义，激活函数的引入为的是增加整个网络的表达能力 (即非线性)，否则，若干线性操作层的堆叠仍然只能起到线性映射的作用，无法形成复杂的函数。下面将介绍几种常见的激活函数。

性质：
（1）非线性：线性激活对于深层神经网络没有作用，因为其作用以后仍然是输入的各种线性变换。
（2）连续可微：梯度下降法的要求。
范围最好不饱和，当有饱和的区间段时，若系统优化进入到该段，梯度近似为 0，网络的学习就会停止。
（3）单调性：当激活函数是单调时，单层神经网络的误差函数是凸的，好优化。
在原点处近似线性，这样当权值初始化为接近 0 的随机值时，网络可以学习得较快，不用调节网络的初始值。

讯享网

5.神经元计算步骤

x1,x2表示输入部分，w1,w2表示权值部分
（1）先将两个输入乘以权值
x1 × w1 = x1(new)
x2 × w2 = x2(new)
（2）把两个结果相加，再加上一个偏置
(x1 × w1) + (x2 × w2) + b
（3）最后将它们经过激活函数处理得到输出
y = f((x1 × w1) + (x2 × w2) + b)
备注：
激活函数的作用： 它就是将无限制的输入转换成可以预测的形式输出。常用的激活函数是sigmoid函数
sigmoid函数： 它的输出介于0和1，我们可以把它理解为将实数R范围内的数亚索到（0，1）以内。正值越大输出越接近1，负向数值越大输出越接近0.
偏置b的作用： 偏置b的作用主要是让函数可以在原点上下，而不局限于一定通过原点（类似于一元函数）
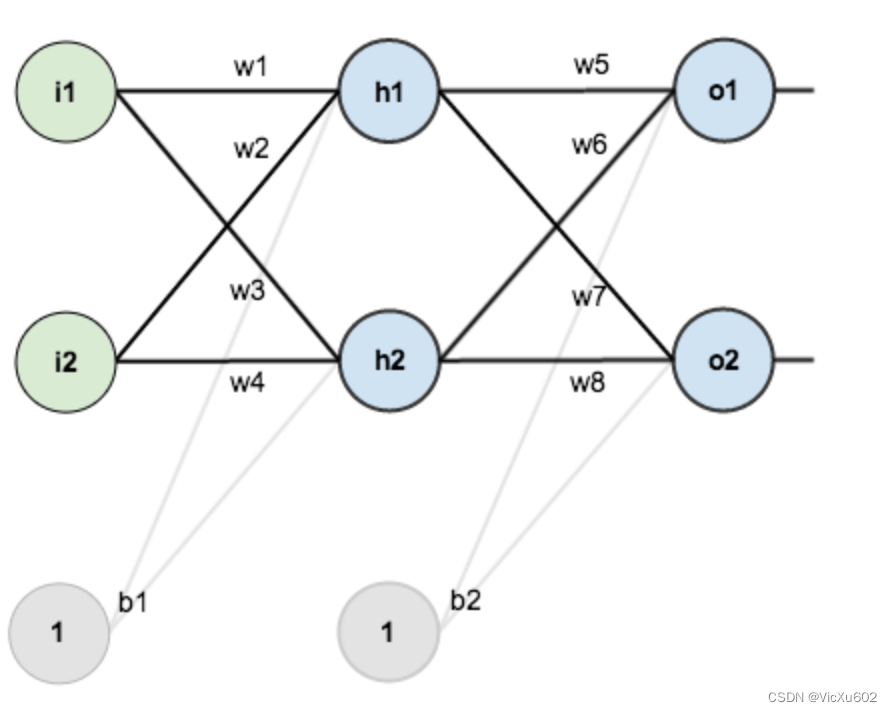
在这里插入图片描述
*该图b1,b2即为偏置

6.由单层神经网络到多层神经网络

（1）两层神经网络：
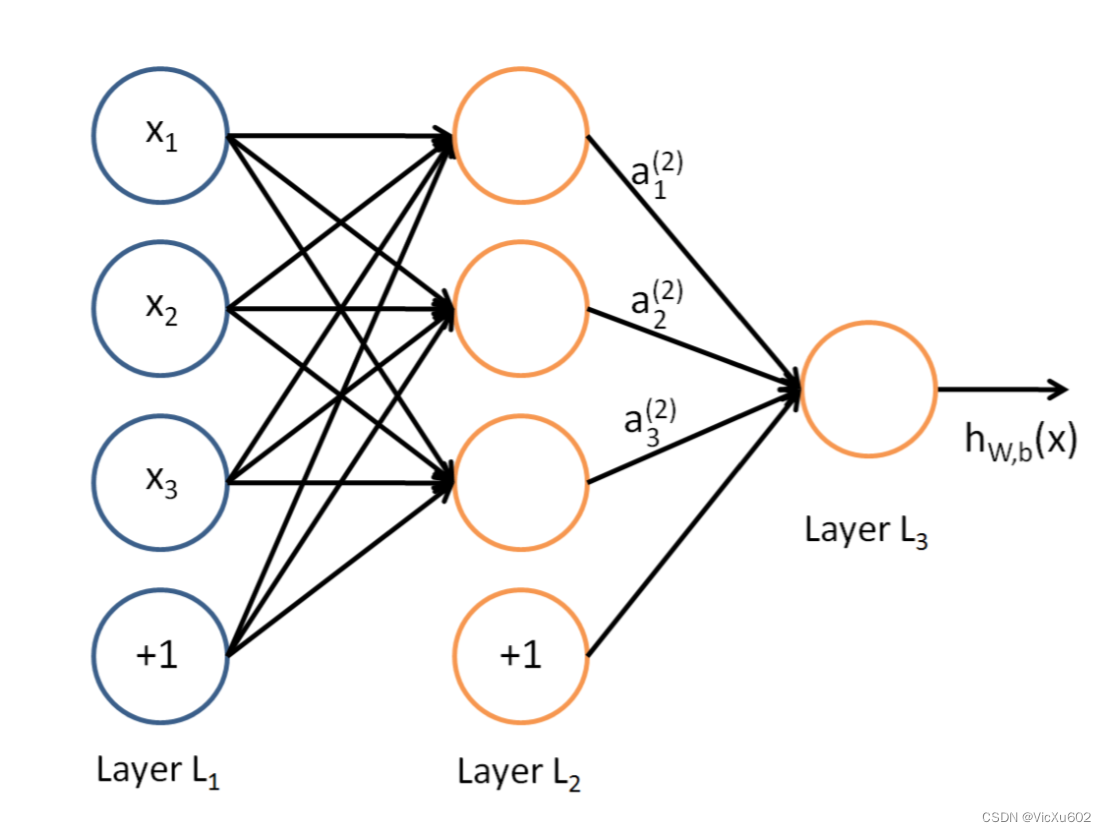
在这里插入图片描述
*如图所示该图为一个两层神经网络

两层神经网络： 除了包含一个输入层和一个输出层以外，还增加了一个中间层（隐层），此时有中间层和输出层两个计算层。最左边为输入层，中间为隐藏层，最右边为输出层。

区别： 与单层神经网络不同，两层神经网络可以无限逼近任意连续函数。也就是说，面对复杂的非线性分类任务，两层神经网络可以很好地分类。
（2）多层神经网络：

在两层神经网络的基础上再增加一个或者更多个隐层，就构成了多层的神经网络，此时计算层的数量为三个或更多。其计算也更为复杂，即
$g (W (1) * a (1)) = a (2)$ $g(W ^{(2)}*a^{(2)})=a^{(3)}$ $g(W ^{(3)}*a^{(3)})=z$

区别：
与两层神经网络不同，随着网络的层数增加，每一层对于前一层次的抽象表示更深入。在神经网络中，每一层神经元学习到的是前一层神经元值的更抽象的表示。例如第一个隐藏层学习到的是 “边缘” 的特征，第二个隐藏层学习到的是由 “边缘” 组成的 “形状” 的特征，第三个隐藏层学习到的是由 “形状” 组成的 “图案” 的特征，最后的隐藏层学习到的是由 “图案” 组成的 “目标” 的特征。

7.代码实现

import numpy as np #定义激活函数，这里使用到的是 Sigmoid 函数 def nonlin(x,deriv=False): if(deriv==True): #定义 Sigmoid 的导数 return x*(1-x) return 1/(1+np.exp(-x)) #Sigomid 函数 #定义输入数据 X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) #print (X.shape) #目标比对模型 y = np.array([[0], [1], [1], [0]]) #print (y.shape) np.random.seed(1) # randomly initialize our weights with mean 0 w0 = 2*np.random.random((3,4)) - 1 w1 = 2*np.random.random((4,1)) - 1 #print (w0) #print (w1) #print (w0.shape) #print (w1.shape) for j in range(60000): #前向传播，l0 为输入层，l1 为隐层，l2 为输出层 l0 = X l1 = nonlin(np.dot(l0,w0)) #矩阵运算 l2 = nonlin(np.dot(l1,w1)) l2_error = y - l2 #打印误差值 if (j% 10000) == 0: print ("Error:" + str(np.mean(np.abs(l2_error)))) #反向传播 l2_delta = l2_error * nonlin(l2,deriv=True) l1_error = l2_delta.dot(w1.T) l1_delta = l1_error * nonlin(l1,deriv=True) #更新权重 alpha = 0.5 #学习率 w1 += alpha * l1.T.dot(l2_delta) w0 += alpha * l0.T.dot(l1_delta)

讯享网

人工神经网络