机器学习笔记【2】：反向传播算法学习

科技前沿 • 2025-01-15 12:00 • 阅读 69

大家好，我是讯享网，很高兴认识大家。

反向传播算法学习

我们利用梯度下降算法来学习权重（weights）和偏置（biases） 那么如何计算代价函数的梯度？ 一个快速计算梯度的算法，就是广为人知的反向传播算法（backpropagation）

讯享网

#背景
反向传播算法最早于上世纪70年代被提出，但是直到1986年，由David Rumelhart, Geoffrey Hinton, 和Ronald Williams联合发表了一篇著名论文之后，人们才完全认识到这个算法的重要性。这篇论文介绍了几种神经网络，在这些网络的学习中，反向传播算法比之前提出的方法都要快。这使得以前用神经网络不可解的一些问题，现在可以通过神经网络来解决。今天，反向传播算法是神经网络学习过程中的关键（workhorse）所在。

#介绍
反向传播算法的核心是一个偏微分表达式 ∂C/∂w ，表示代价函数 C 对网络中的权重 w （或者偏置 b ）求偏导。这个式子告诉我们，当我们改变权重和偏置的时候，代价函数的值变化地有多快。
这个式子的每一个部分都有自然的，直觉上的解释。
因此，反向传播不仅仅是一种快速的学习算法，它能够让我们详细深入地了解改变权重和偏置的值是如何改变整个网络的行为的。这是非常值得深入学习的。

讯享网

#引入学习认识
我们用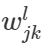在这里插入图片描述来表示从第l−1层的第k个神经元到第l层的第j个神经元的连接的权重
例如，下图展示了从第二层的第四个神经元到第三层的第二个神经元的连接的权重：

这一小节待补充！！！！！！

#关于代价函数的两个假设
反向传播算法的目标是计算代价函数 C 对神经网络中出现的所有权重 w 和偏置 b 的偏导数 ∂C/∂w 和 ∂C/∂b 。。为了使反向传播工作，我们需要对代价函数的结构做两个主要假设。
（1）代价函数能够被写成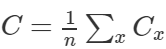在这里插入图片描述的形式，其中 Cx 是每个独立训练样本 x 的代价函数。在代价函数为平方代价函数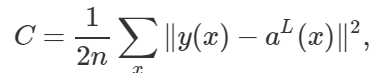的情况下，一个训练样本的代价是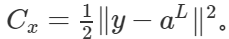
#为什么要做上述假设？
我们需要上述假设的原因是，反向传播实际上是对单个训练数据计算偏导数 ∂Cx/∂w 和 ∂Cx/∂b 。然后通过对所有训练样本求平均值获得 ∂C/∂w 和 ∂C/∂b 。事实上，有了这个假设，我们可以认为训练样本 x 是固定的，然后把代价 Cx 去掉下标表示为 C

(2)代价函数可以写成关于神经网络输出结果的函数
在这里插入图片描述

机器学习笔记【2】：反向传播算法学习

相关推荐