正交化
在优化算法的迭代过程中,可能会存在很多个可以改善的方面。
假设你同时修改多个进行优化,那么不能直接从结果中看出。你要做的类似于控制变量法,一次修改一个看看是否有用。
贝叶斯最优误差
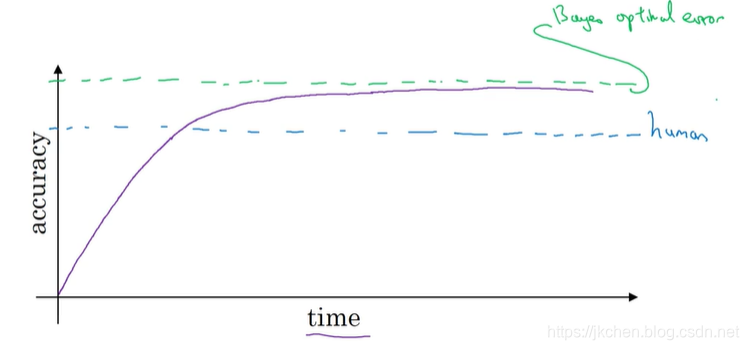
在算法的不断改善的迭代过程中,存在这样的情况:如果你的准确率劣于人类表现,那么改善速度会很快。但是当超过人类表现后会变慢。误差因为实际情况的原因,存在一个上限。例如语言识别中杂音很重,根本听不清楚,那么这种情况下一定存在误差。这个上限称为贝叶斯最优误差。
可避免偏差、方差
假设你的验证集误差为10%,贝叶斯误差1%,测试集误差为15%,那么存在9%的可避免偏差(要拟合的更好),5%的可避免方差(存在过拟合问题)。

那么显然可避免偏差较大,根据正交化的思想,我们尝试先减小偏差,例如加大梯度下降执行次数等。
人类表现
在一些领域,例如计算机视觉,人类表现非常好,近乎接近极限。那么在这种情况下,我们用人类表现去代替贝叶斯误差。
有一个问题,一个普通人的误差是10%,专家的误差是5%,一群专家讨论的误差是2%。那么我们用来代替贝叶斯误差的人类误差应该是2%。
计算机在感知方面超越人类很难,但是在基于数据、经验的问题解决上很容易强于人类。
例如,给你推送电影、淘宝首页、判断一件事发生的概率、围棋的下法。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/47445.html