大家好，我是讯享网，很高兴认识大家。

欢迎大家关注我的B站：

偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)

目录

1 DWA算法简介

2 运动学模型

2.1直线轨迹模型

2.2 圆弧直线模型

2.3 车辆二自由度模型

3 DWA 算法整体框架

3.1 速度搜索空间

3.2 代价函数

3.3 搜索流程

4 DWA算法matlab实现

4.1 动画

4.2 核心算法部分

4.3 随机生成障碍物

4.4 dist 函数

4.5 distance 函数

---

1 DWA算法简介

DWA算法第一次提出应该是1997年，发在了《IEEE Robotics and Automation Magazines》上，有兴趣的读者可以参考原始论文https://www.csie.ntu.edu.tw/~b92025/paper/Dyanmic_Window.pdf。对于无法预测的动态障碍物，DWA算法可以较好地解决动态避障这个问题。DWA算法的优点是考虑到速度和加速度的限制，同时只有无碰撞的轨迹会被考虑，因此，采样的速度即形成了一个动态窗口。在这个动态窗口中又很多条可行轨迹，通过自行设计一个评价函数，挑选出一条最优轨迹，经过重复迭代，不断地搜索当前最优轨迹，最终到达目标点。

2 运动学模型

2.1直线轨迹模型

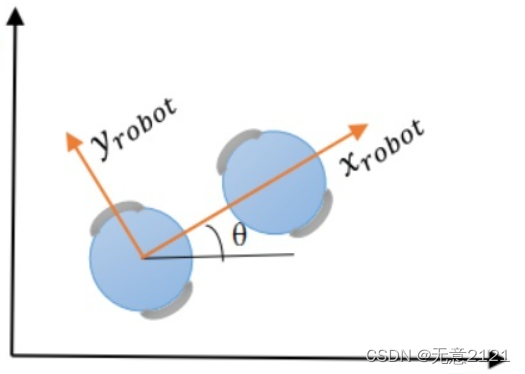
在机器人或智能车辆运动的极短时间内，轨迹可以近似看作匀速直线运动，模型非常简单，但采样时间过短造成计算复杂度过高，计算缓慢。下图为世界坐标系与机器人坐标系示意图

讯享网

若机器人不是全向运动的：

那么机器人只能前进和旋转，前进速度方向与机器人航向角保持一致，同时控制变量是控制前进的加速度与控制转向的角加速度，运动差分方程如下

若机器人是全向运动的：

那么机器人有任意方向的速度，也就是不一定与航向角保持一致，所以速度可以在机器人坐标系下分解为横向速度与纵向速度，同时控制变量是控制前进的横向加速度与纵向加速度与控制转向的角加速度，运动差分方程如下

这个微分方程可以看作是第一个微分方程调整而来，增加了机器人纵向速度在世界坐标系下的投影。在ROS的轨迹推演中就使用的该公式，base_local_planner的轨迹采样程序也是使用的该公式。

2.2 圆弧直线模型

在极短时间内近似处理运动为匀速直线运动时不符合实际，不符合机器人和车辆运动学的，因此我们采取更准确的运动学模型，

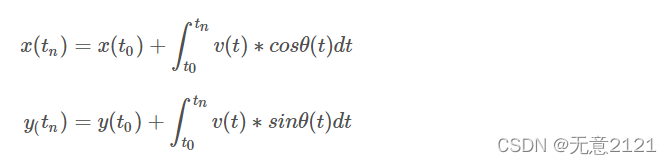
引入加速度与角加速度，初始速度与初始角速度与初始航向角，可完善上述公式

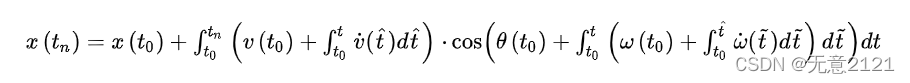
同理可得y方向上的位置，这个公式可见机器人可以由控制变量与初始状态进行控制未来的状态。由于机器人内部结构原因，其加速度不能够连续变化，因此将t0到tn看作是很多个时间片，积分可转换为求和，将t0到tn分成n个切片，当n足够大时，在每个切片中加速度与角加速度不变。设   

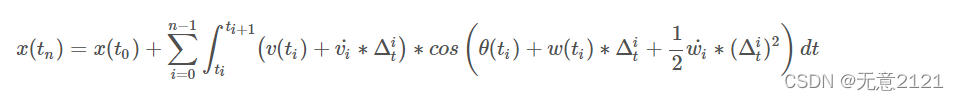
但是这个公式仍不能决定机器人具体的驾驶方向，对于障碍物与机器人轨迹的交点也很难求出，继续进行简化，当n足够大时，角加速度和加速度可近似看作对角速度和速度不起作用

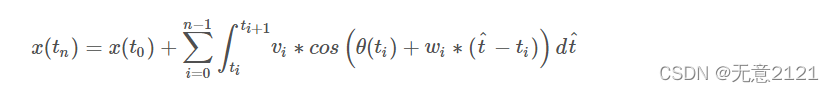
简化为

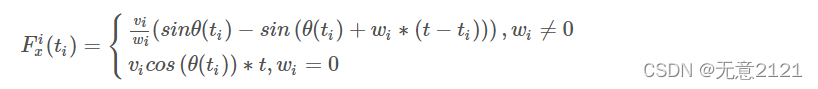
y轴上的方程同理可得，当wi 等于0的时候，轨迹为直线，当wi 不等于0的时候，轨迹为圆弧

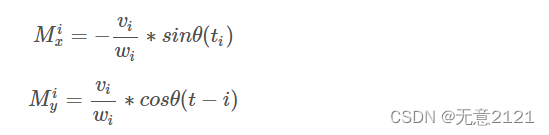
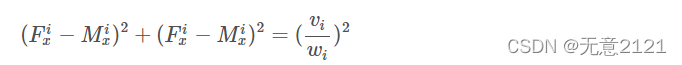
上述公式可以求出机器人的轨迹，即轨迹可以通过一系列分段的圆弧和直线来拟合。这种圆弧直线模型也是DWA算法原始论文中采用的运动学模型。

2.3 车辆二自由度模型

模型的假设：

（1）车辆行驶于平坦路面，忽略车辆在垂直于地面方向上的运动；

（2）忽略车辆受到的空气阻力以及地面侧向摩擦力；

（3）车辆与地面始终保持良好的滚动摩擦；

（4）车辆为刚体，忽略车身悬架结构的影响。

二自由度模型忽略左右两轮的转动角速度与角加速度差异，将车辆的两只前轮与后轮以车辆的纵轴方向合并为虚拟单轮，因此二自由度模型也称为 bicycle 模型。运动学微分方程组如下

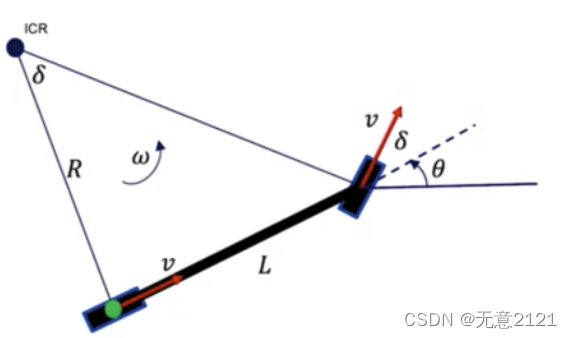
3 DWA 算法整体框架

3.1 速度搜索空间

（1）轨迹以圆弧为主，该轨迹由采样速度(v,w)决定，采样速度(v,w)需在可行范围内，这些速度构  成一个初始的速度搜索空间。

（2）有一个实时更新的最大速度限制，保证在最大加速度下能在最近的障碍物前停下来。                     

dist(v,w)为机器人轨迹上与最近的障碍物的距离。

（3）由于加速度有一个范围限制，所以最大加速度或负方向最大加速度一定时间内能达到的速度  才会被保留，这也就形成了动态窗口。

这里的(v0,w0)是当前的速度。

综上所述，搜索空间为

下图是搜索空间下的采样轨迹示例

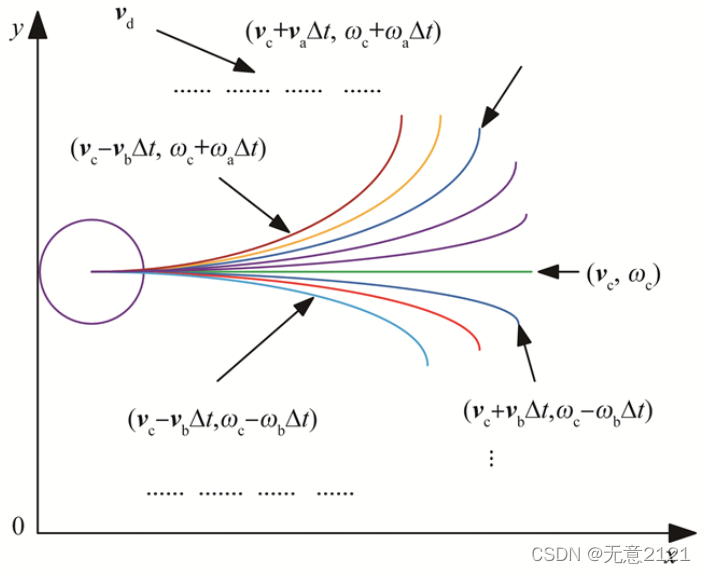
3.2 代价函数

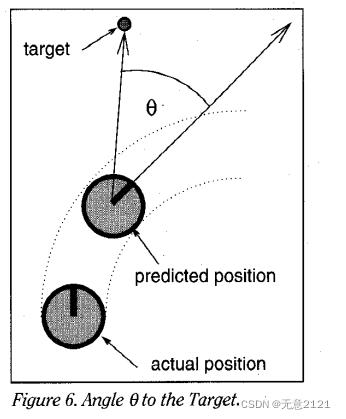
（1）这里的heading代表航向角和实际机器人与目标点连线的角度偏差，目的是纠正机器人航向，最终能快速到达目标点。计算时通常用余弦函数或者反三角函数。

（2）这里的dist代表机器人轨迹上与最近的障碍物的距离，目的是与障碍物保持距离。计算时一般还要设置一个最大值，当超过这个距离时，就让dist恒等于这个最大值，防止距离障碍物越远越好的情况出现。

（3）这里的vel代表机器人的速度，目的是让机器人以较快速度到达目标点，同时防止为了避障陷入速度极小的情况。计算时一般用速度的绝对值。

•  三个参数代表权重，不同情况的环境可能需要不同的权重，自行调参。同时为了消除量纲，采取权重归一化。
•  使得三个部分的权重更加平滑，使得轨迹与障碍物之间保持一定的间隙。
• 当机器人陷入局部最优时（即不存在路径可以通过），使其原地旋转，直到找到可行路径。
• 安全裕度：在路径规划时，设定一安全裕度，即在路径和障碍物之间保留一定间隙，且该间隙随着速度增大线性增长。

 下图为评价函数的示例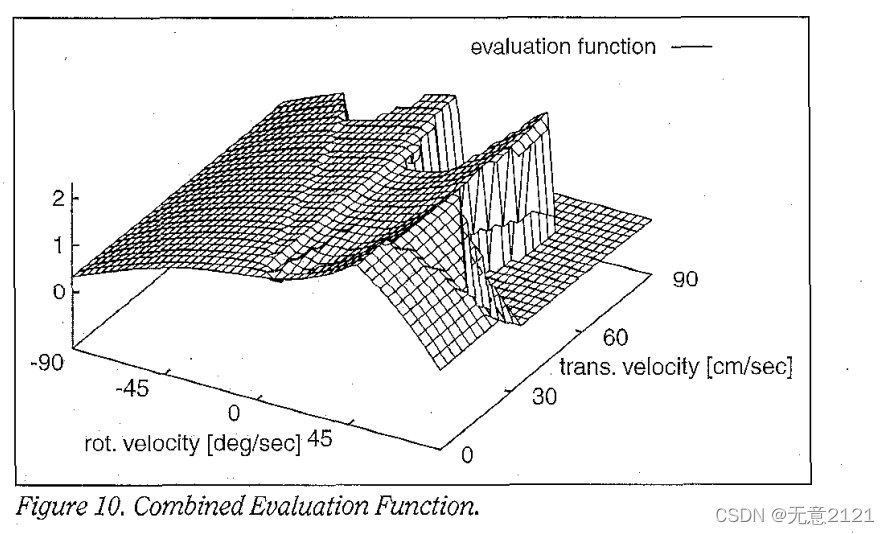

3.3 搜索流程

DWA算法原理是先建立3.1所述的三种约束下的搜索空间，然后以一定分辨率 (可以自行调整) 对(v,w)进行采样，再对采样的(v,w)计算代价函数，选出时间间隔 t 内的最优的轨迹，将机器人以此最优轨迹对应的(v,w)移动 t/n 段时间，n由自己指定 (我的理解是确实挑出了较优的轨迹，保险起见，我只移动较优轨迹的一部分，以便于后续我再根据所处状况进行调整)，接着重复上述步骤，最后在机器人与目标点距离小于某个值时停止搜索。

4 DWA算法matlab实现

4.1 动画

4.2 核心算法部分

超参数自行调整，运动学模型可以根据本篇文章介绍的自行调整

clc clear all %如下初始化范围均可自行调整 a=[-1,1];%加速度范围 b=[-20,20];%角加速度范围 vfan=[0.2,0.5];%速度范围 wfan=[-20,20];%角速度范围 v=0.4;%初始速度 o=pi/4;%初始化航向角 dt=0.1;%时间间隔 t=0; wxx=0;%初始角速度 x=0;y=0;%机器人实时坐标 B=[90,90];%目标点坐标 k1=[0];k2=[0];%储存路径 [f,n1]=ob(5);%随机生成障碍物，个数自行调整，个数过多不易生成 while distance(x,y,B(1),B(2))>2 %自行设定与目标点的截止距离 va=sqrt(2*a(2)*dist(x,y,f,n1));%撞上障碍物的最大速度 wa=sqrt(2*b(2)*dist(x,y,f,n1)); max=0; %速度在加速或减速可达的范围内 if va<v+dt*a(2) vmax=va; vmin=v+dt*a(1); else vmax=v+dt*a(2); vmin=v+dt*a(1); end if vmax>vfan(2) vmax=vfan(2); end if vmin<vfan(1) vmin=vfan(1); end if wa<wxx+dt*a(2) wmax=wa; wmin=wxx+dt*b(1); else wmax=wxx+dt*b(2); wmin=wxx+dt*b(1); end if wmax>wfan(2) wmax=wfan(2); end if wmin<wfan(1) wmin=wfan(1); end for v=vmin:0.3:vmax %采样频率自行调整 for w=wmin:0.3:wmax%采样频率自行调整 Fxx=x;Fyy=y;oxx=o;%保存起点位置 max1=10;%根据障碍物大小进行调整 min1=10000; while t<12 %评估轨迹时的时间间隔，可自行调整 Fx=x;Fy=y; x=x+v*dt*cos(o);%位置更新 y=y+v*dt*sin(o); if dist(x,y,f,n1)<min1 %dist等于整条轨迹中离障碍物最近的距离 min1= dist(x,y,f,n1); end if min1>=max1 %在距离障碍物距离大于max1时，dist恒等于max1 max1=max1; else max1=min1; end o=o+w*dt*0.1;%航向角更新 t=t+dt; %plot([Fx,x],[Fy,y],'b-');hold on;xlim([0,100]);ylim([0,100]); %这一语句是来测试一个速度不同角速度下的采样轨迹是否合理 end pinjia1=abs(o-atan((90-y)/(90-x)));%航向角偏差 if pinjia1>pi pinjia1=(pi-(2*pi-pinjia1))*70;%转化到0~pi范围并乘权重 else pinjia1=(pi-pinjia1)*70; end pinjia2=max1*190;%可调整参数 pinjia3=abs(v)*90;%可调整参数 pinjia=pinjia1+pinjia2+pinjia3; if pinjia>max max=pinjia; vfinal=v;wfinal=w; %不断选取最优评价函数的(v,w) end t=0; x=Fxx;y=Fyy;o=oxx;%起点位置不能丢失，要保存 end end t=0;x=Fxx;y=Fyy;o=oxx; while t<1 %实际移动时的时间间隔 Fx=x;Fy=y; x=x+vfinal*dt*cos(o); y=y+vfinal*dt*sin(o); o=o+wfinal*dt*0.1; t=t+dt; %plot([Fx,x],[Fy,y],'b-');hold on;xlim([0,100]);ylim([0,100]); end %plot(x,y,'ro');hold on;xlim([0,100]);ylim([0,100]); v=vfinal;wxx=wfinal; k1=[k1,x]; k2=[k2,y]; end %显示动画 f1=size(k1); for i=1:f1(2) plot(k1(i),k2(i),'ro'); pause(0.0001);hold off;%动画速度自行调整 aplha=0:pi/40:2*pi; for j=1:n1 r=f(3*j); x=f(3*j-1)+r*cos(aplha); y=f(3*j-2)+r*sin(aplha); plot(x,y,'b-');hold on plot(0,0,'go');hold on; plot(90,90,'ko');hold on; hold on; end end

讯享网

4.3 随机生成障碍物

讯享网function [f,n1]=ob(n) f=[];%储存障碍物信息 n1=n;%返回障碍物个数 p=0; for i=1:n k=1; while(k) D=[rand(1,2)*60+15,rand(1,1)*1+3];%随机生成障碍物的坐标与半径，自行调整 if(distance(D(1),D(2),90,90)>(D(3)+5)) %与目标点距离一定长度，防止过多阻碍机器人到达目标点 k=0; end for t=1:p %障碍物之间的距离不能过窄，可自行调整去测试 if(distance(D(1),D(2),f(3*t-2),f(3*t-1))<=(D(3)+f(3*t)+20)) k=1; end end end %画出障碍物 aplha=0:pi/40:2*pi; r=D(3); x=D(1)+r*cos(aplha); y=D(2)+r*sin(aplha); plot(x,y,'b-'); axis equal; hold on; xlim([0,100]);ylim([0,100]); f=[f,D]; p=p+1;%目前生成的障碍物个数 end hold all;

4.4 dist 函数

function f=dist(a,b,D,n) min=10000;% for i=1:n if abs(distance(a,b,D(3*i-2),D(3*i-1))-D(3*i))<min min=distance(a,b,D(3*i-2),D(3*i-1))-D(3*i); end end f=min;

4.5 distance 函数

讯享网function f=distance(x,y,x1,y1) f=sqrt((x-x1)^2+(y-y1)^2);