一刷271-二分+dfs -778. 水位上升的泳池中游泳（h）

科技前沿 • 2025-03-30 19:01 • 阅读 47

大家好，我是讯享网，很高兴认识大家。

题目： 在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。 当开始下雨时，在时间为 t 时，水池中的水位为 t 。 你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。 假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。 当然，在你游泳的时候你必须待在坐标方格里面。 你从坐标方格的左上平台 (0，0) 出发。 返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。

讯享网

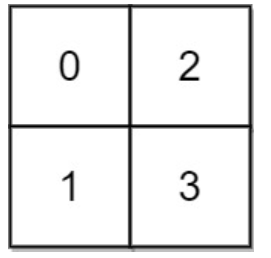
在这里插入图片描述
讯享网

讯享网输入: grid = [[0,2],[1,3]] 输出: 3 解释: 时间为0时，你位于坐标方格的位置为 (0, 0)。 此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。 等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

在这里插入图片描述

输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] 输出: 16 解释: 最终的路线用加粗进行了标记。 我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的 提示: n == grid.length n == grid[i].length 1 <= n <= 50 0 <= grid[i][j] < n2 grid[i][j] 中每个值 均无重复 -------------------- 思路： 注意题目中的重要信息：假定你可以 瞬间移动 无限距离，游动不耗时。 当前这个问题就转换成为：找一个时刻 t，使得这个二维网格上数值 小于等于 t 的部分， 存在一条从左上角到右下角的路径。 即：经过了时间 t 以后，可以瞬间从左上角（坐标 [0, 0]）游到右下角（坐标 [N - 1, N - 1]） ------------ DFS加二分查找 正常的深度优先搜索会导致超时 因此引入二分查找降低时间复杂度，根据每次搜索的结果不断更新边界值即可 ------------------ class Solution { 
    private int row; private int col; private int[][] dir = { 
   { 
   1, 0}, { 
   -1, 0}, { 
   0, 1}, { 
   0, -1}}; public int swimInWater(int[][] grid) { 
    row = grid.length; col = grid[0].length; int left = 0; int right = 2500; while (left <= right) { 
    int mid = left + ((right - left) >> 1); if (!dfs(0,0,mid, grid, new boolean[row][col])) { 
    left = mid + 1; }else { 
    right = mid - 1; } } return left; } private boolean dfs(int x, int y, int target, int[][] grid, boolean[][] visited) { 
    if (x == row - 1 && y == col - 1) return true; visited[x][y] = true; for (int[] d : dir) { 
    int nx = x + d[0]; int ny = y + d[1]; if (0 <= nx && nx < row && 0 <= ny && ny < col && !visited[nx][ny]) { 
    if (Math.max(grid[nx][ny],grid[x][y]) > target) { 
    continue;//! 进行下次循环 } if (dfs(nx, ny, target, grid, visited)) { 
    return true; } } } return false; } }

一刷271-二分+dfs -778. 水位上升的泳池中游泳（h）

相关推荐