若函数f(x)在[a,b]上可积，则f(x)在[a,b]上必有界。可积的必要条件。
可积 的充分条件：
1.函数在闭区间上连续
2.函数在闭区间上有界且只有有限个间断点
3.函数在闭区间上单调。
在一元函数中，可微一定连续，且连续一定可积。反之不成立。
一元函数在闭区间上连续、可导、可微、可积、有界关系图：
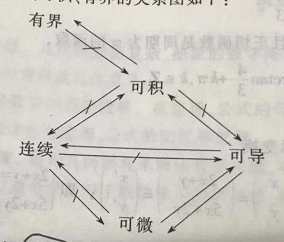
二更：
若不是闭区间
则，可导必连续，但是可导不一定有界，不一定一致连续
比如，f(x)=1/x
2025年黎曼可积
黎曼可积若函数 f x 在 a b 上可积 则 f x 在 a b 上必有界 可积的必要条件 可积 的充分条件 1 函数在闭区间上连续 2 函数在闭区间上有界且只有有限个间断点 3 函数在闭区间上单调 在一元函数中 可微一定连续 且连续一定可积 反之不成立 一元函数在闭区间上连续 可导 可微 可积
大家好，我是讯享网，很高兴认识大家。
2025年2023.2.20学习日志
上一篇
2025-03-02 22:18
参考文献中英文人名的缩写规则
下一篇
2025-02-27 22:28
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请联系我们，一经查实，本站将立刻删除。
如需转载请保留出处：https://51itzy.com/kjqy/43728.html