【SCPC第三次对抗赛】

科技前沿 • 2025-02-27 20:14 • 阅读 49

大家好，我是讯享网，很高兴认识大家。

SCPC第三次对抗赛

---hp枫落出题部分

讯享网

J:雨散枫飘佳靥去

链接: link

先从题目中提取关键信息：r-l+1= $\sum_{i=l}^{r} a{_i}$
求符合此条件的区间[l,r]的个数

我们用sum[N]代表数组a的前缀和数组。
那么我们将式子进行转化
r-l+1=sum[r]-sum[l-1]
->sum[r]-r=sum[l-1]-l-1
设数组c[i]=sum[i]-i。
那么写法就很显然了假如当前位置是j 这个位置对答案的贡献就是
cnt[sum[j]-j] (cnt[x]代表在j之前 x出现的次数)

下面展示一些 主要代码。

讯享网 ll ans=0; ll n;cin>>n; FOR(i,1,n){ 
    cin>>a[i]; sum[i]=sum[i-1]+a[i]; } map<ll,ll>mp; mp[]=1; FOR(i,1,n){ 
    ans+=mp[sum[i]-i+]; mp[sum[i]-i+]++; } cout<<ans<<endl;

I:凢凢传之勾引小学妹

H:严佬的后宫(hard version)

原题链接： link

注意：easy版本是hard的**版就不单独讲了

tips: 题面说了n<=m
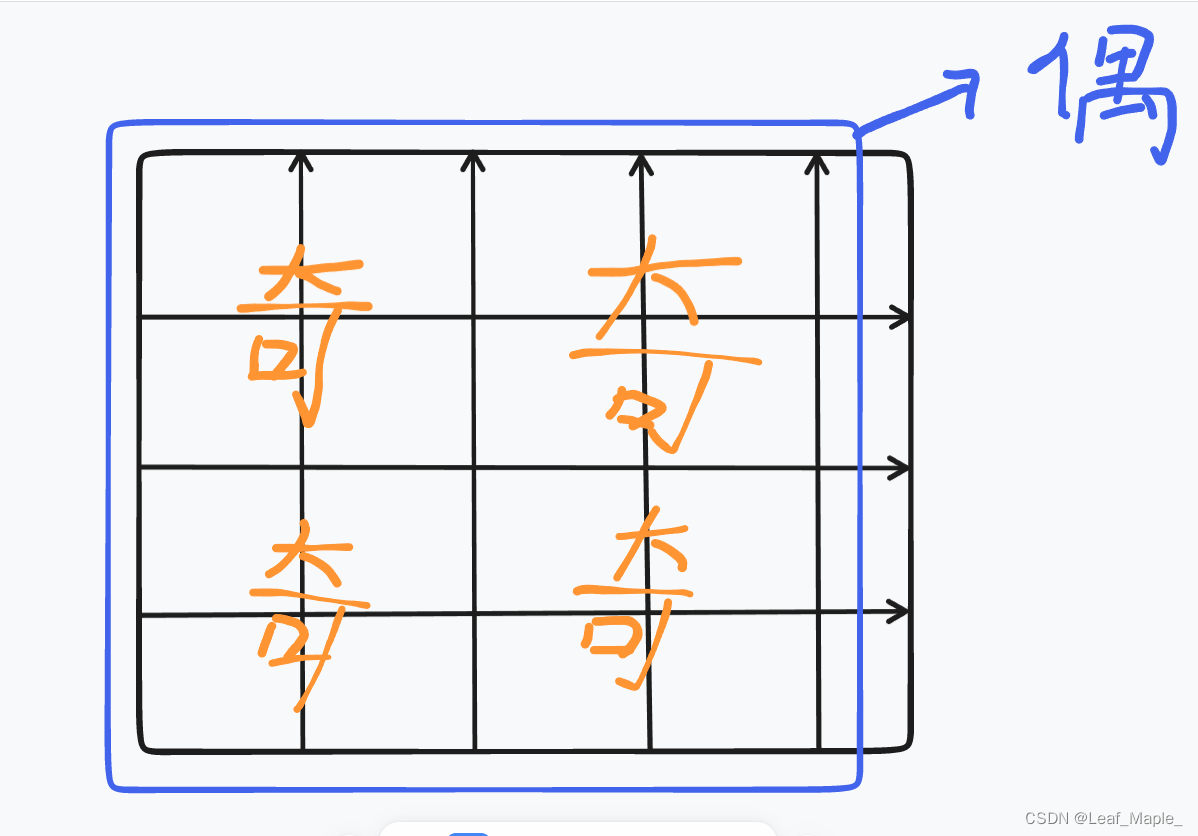
首先很显然如果矩阵的n>=4 那么这个矩阵一定能被拆为诺干个22的小矩阵
由于每个22的小矩阵1的个数都是奇数那么4个小矩阵和在一起1的个数一定是偶数
请添加图片描述
讯享网

 if(n>=4){ 
    cout<<-1<<endl; return 0; }

讯享网 if(n==1){ 
    cout<<0<<endl; return 0; ｛

这个肯定不需要解释吧！

二、再考虑n=2 也就是easy version

我们先考虑第一列其实只有两种情况
1：第一列有奇数个1
2：第一列有偶数个1
为什么呢？因为当知道第一列的奇偶性后第二列的是一定的以此类推第三列也是一样的所以只要我们暴力计算下2种情况就行了！

 void slove2(){ 
    int ans1 = 0,ans2 = 0; for(ll i=1;i<=m;i+=2){ 
    if(st[i]==0||st[i]==3)ans1++; if((st[i+1]==1||st[i+1]==2)&&i+1<=m)ans1++; } for(ll i=1;i<=m;i+=2){ 
    if(st[i]==1||st[i]==2)ans2++; if((st[i+1]==0||st[i+1]==3)&&i+1<=m)ans2++; } cout<<min(ans1,ans2)<<'\n'; }

tips：st储存的是01的状态

讯享网 FOR(j,1,m){ 
    ll x=0; FOR(i,1,n){ 
    if(i)x<<=1; if(a[i][j]==1)x++; } st[j]=x; } }

三、n=3的情况
很显然3*3的矩阵是可以满足题目条件的，我们仍旧考虑列首先3行的01组合有8种方式（000 001 010 011 100 101 110 111, 注意这里的是竖着的1列可能的情况）
假设当前是第 i 列显然第 i 列的每种可能一定是从第 i-1 列转移过来的，所以这里我们考虑dp
f[i][j]=f[i-1][p]+（cnt）(0<=j<=8)
cnt为让让这两列满足条件时候前i-1列需要的最少改变次数
注：此时前i-1列是满足条件的

这里画个图再强调一下什么叫两列满足条件：
例如010 就只能从111和000转移过来，因为只有这样才满足每个2*2的矩阵1的个数为奇数。
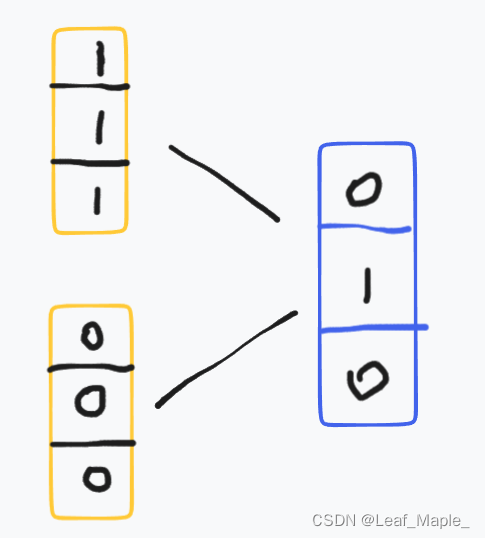
在这里插入图片描述
我这里是用讲01串进行状态压缩来dp的也就是状压dp

tips:bp是处理出这两个状态之间需要操作的变化函数

vector<ll>g[8]; ll f[N][10]; void slove3(){ 
    g[0]={ 
   2,5};g[1]={ 
   4,3};g[2]={ 
   0,7};g[3]={ 
   1,6}; g[4]={ 
   1,6};g[5]={ 
   0,7};g[6]={ 
   3,4};g[7]={ 
   2,5}; for(ll i=0;i<8;i++)f[1][i]=bp(i^st[1]); for(ll i=2;i<=m;i++){ 
    for(ll j=0;j<8;j++){ 
    f[i][j]=min(f[i-1][g[j][0]]+bp(j^st[i]), f[i-1][g[j][1]]+bp(j^st[i])); } } ll ans=1e9; for(ll i=0;i<8;i++)ans=min(ans,f[m][i]); cout<<ans<<endl; } }

【SCPC第三次对抗赛】

SCPC第三次对抗赛

J:雨散枫飘佳靥去

I:凢凢传之勾引小学妹

H:严佬的后宫(hard version)

相关推荐