1.威尔逊定理:
当且仅当p为素数时:( p -1 )! ≡ p-1 ( mod p )
即若p为质数,则p能被(p-1)!+1整除
2.欧拉定理:
欧拉定理:也称费马-欧拉定理
若n,a为正整数,且n,a互质,即gcd(a,n) = 1,则a^φ(n) ≡ 1 (mod n)
φ(n) 是欧拉函数:
欧拉函数是求 1到n-1 中 与n互质的数 的数目
如果n是质数,那么1到n-1所有数都是与n互质的,所以φ(n) = n-1
欧拉公式:
e的ix次方 = cosx + isinx
把x用π带进去,变成
e的iπ次方= -1
3.孙子定理(中国剩余定理)
用现代数学的语言来说明的话,中国剩余定理给出了以下的一元线性同余方程组:
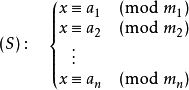
中国剩余定理说明:假设整数m1,m2, ... ,mn两两互质,则对任意的整数:a1,a2, ... ,an,方程组 (S)有解
4.费马小定理:
假如p是质数,若p不能整除a,则 a^(p-1) ≡1(mod p),若p能整除a,则a^(p-1) ≡0(mod p)。
或者说,若p是质数,且a,p互质,那么 a的(p-1)次方除以p的余数恒等于1
参考自:http://www.cnblogs.com/linyujun/p/5194142.html


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/43541.html