在现实生活中，有许多应用场景会包含很多点以及点点之间的连接，而这些应用场景我们都可以用即将要学习的图这种数据结构去解决。

1、图的定义及分类

图是由一组顶点和一组能够将两个顶点相连的边组成的

讯享网

 图的分类：

按照连接两个顶点的边的不同，可以把图分为以下两种：

2、无向图

1、图的相关术语

相邻顶点：

当两个顶点通过一条边相连时，我们称这两个顶点是相邻的，并且称这条边依附于这两个顶点。

度：

某个顶点的度就是依附于该顶点的边的个数

子图：

是一幅图的所有边的子集(包含这些边依附的顶点)组成的图；

路径：

是由边顺序连接的一系列的顶点组成

环：

是一条至少含有一条边且终点和起点相同的路径

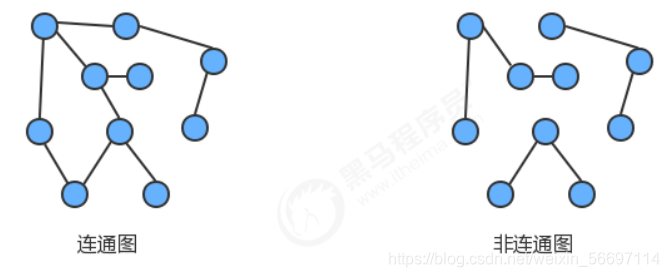
 连通图：

如果图中任意一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为连通图

 连通子图：

一个非连通图由若干连通的部分组成，每一个连通的部分都可以称为该图的连通子图

 2、图的存储结构

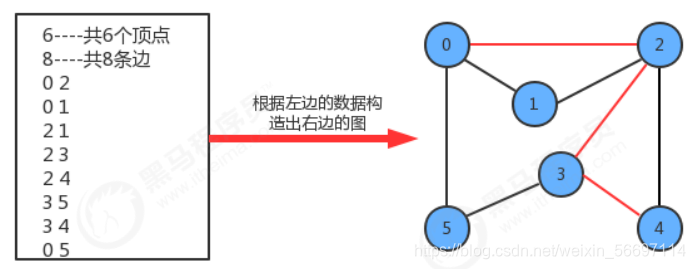
要表示一幅图，只需要表示清楚以下两部分内容即可：

1. 图中所有的顶点；

2. 所有连接顶点的边；

常见的图的存储结构有两种：邻接矩阵和邻接表

1、邻接矩阵

1. 使用一个V*V的二维数组int[V][V] adj,把索引的值看做是顶点；

2. 如果顶点v和顶点w相连，我们只需要将adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。

很明显，邻接矩阵这种存储方式的空间复杂度是 V^2的，如果我们处理的问题规模比较大的话，内存空间极有可能不够用。

2、邻接表

1.使用一个大小为V的数组 Queue[V] adj，把索引看做是顶点；

2.每个索引处adj[v]存储了一个队列，该队列中存储的是所有与该顶点相邻的其他顶点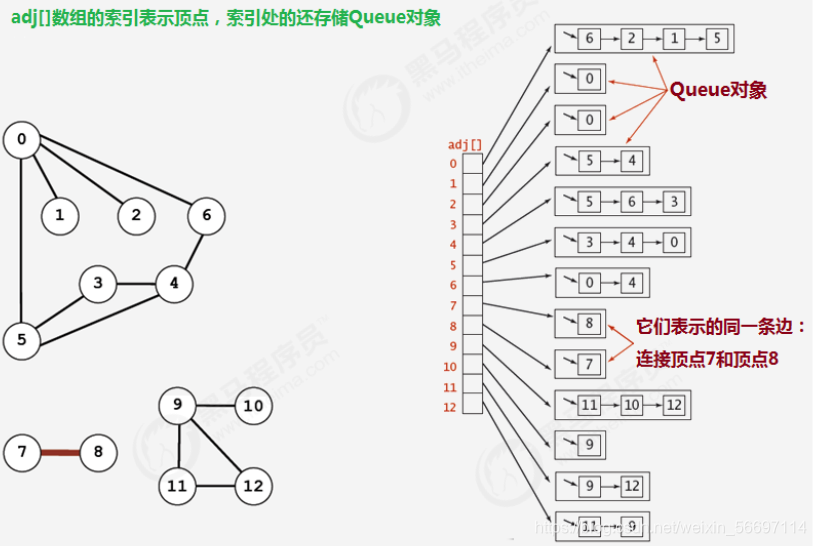

 很明显，邻接表的空间并不是是线性级别的，所以后面我们一直采用邻接表这种存储形式来表示图。

3、实现

package graph; import xianxing.Queue; //图 public class Graph { //顶点数目 private final int V; //边的数目 private int E; //邻接表 private Queue<Integer>[] adj; public Graph(int V){ this.V = V; this.E = 0; this.adj = new Queue[V]; for(int i=0; i<adj.length; i++){ adj[i] = new Queue<>(); } } //获取顶点数目 public int V(){ return V; } //获取边的数目 public int E(){ return E; } //向图中添加一条边 v-w public void addEdge(int v, int w){ adj[v].enqueue(w); adj[w].enqueue(v); E++; } //获取和顶点v相邻的所有顶点 public Queue<Integer> adj(int v){ return adj[v]; } } 

4、图的搜索

在很多情况下，我们需要遍历图，得到图的一些性质，例如，找出图中与指定的顶点相连的所有顶点，或者判定某个顶点与指定顶点是否相通，是非常常见的需求。有关图的搜索，最经典的算法有深度优先搜索和广度优先搜索，接下来我们分别讲解这两种搜索算法。

1、深度优先搜索

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找兄弟结点。

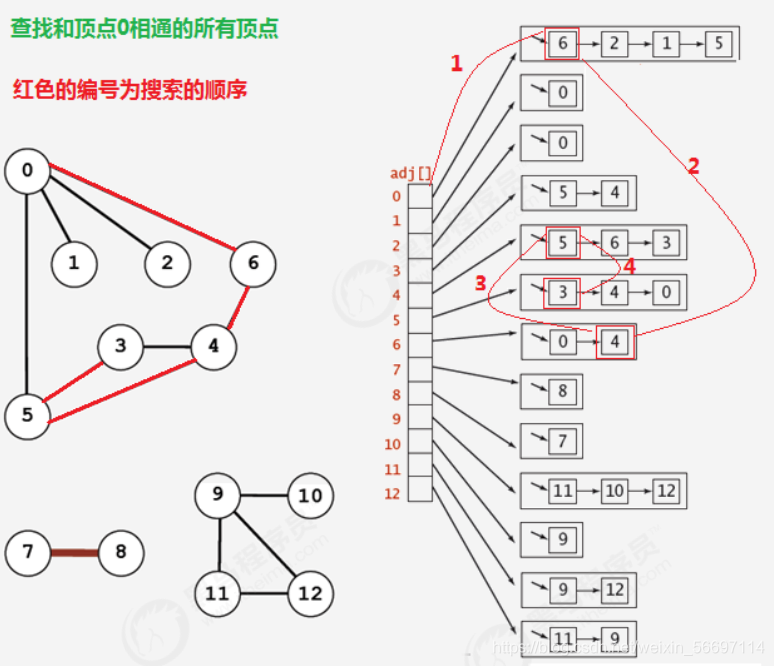
很明显，在由于边是没有方向的，所以，如果 4和5顶点相连，那么4会出现在5的相邻链表中，5也会出现在4的相邻链表中，那么为了不对顶点进行重复搜索，应该要有相应的标记来表示当前顶点有没有搜索过，可以使用一个布尔类型的数组 boolean[V] marked,索引代表顶点，值代表当前顶点是否已经搜索，如果已经搜索，标记为true，如果没有搜索，标记为false；

讯享网package graph; public class DepthFirstSearch { //索引代表顶点，值表示当前顶点是否已经被搜索 private boolean[] marked; //记录有多少个顶点与s顶点相通 private int count; //构造深度优先搜索对象，使用深度优先搜索找出G图中s顶点的所有相邻顶点 public DepthFirstSearch(Graph G,int s){ this.marked = new boolean[G.V()]; this.count = 0; dfs(G,s); } //使用深度优先搜索找出G图中v顶点的所有相通顶点 private void dfs(Graph G, int v){ marked[v] = true; for(Object w : G.adj(v)){ if(!marked[(int) w]){ dfs(G, (int) w); } } count++; } //判断w顶点与s顶点是否相通 public boolean marked(int w){ return marked[w]; } //获取与顶点s相通的所有顶点的总数 public int count(){ return count; } } 

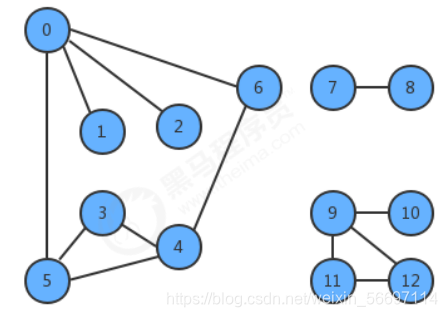
package test; import graph.DepthFirstSearch; import graph.Graph; public class DepthFirstSearchTest { public static void main(String[] args) { Graph graph = new Graph(13); graph.addEdge(0,5); graph.addEdge(0,1); graph.addEdge(0,2); graph.addEdge(0,6); graph.addEdge(5,3); graph.addEdge(5,4); graph.addEdge(3,4); graph.addEdge(4,6); graph.addEdge(7,8); graph.addEdge(9,11); graph.addEdge(9,10); graph.addEdge(9,12); graph.addEdge(11,12); DepthFirstSearch search = new DepthFirstSearch(graph,0); System.out.println("相通的顶点数量："+search.count()); System.out.println("5是否相通："+search.marked(5)); System.out.println("7是否相通："+search.marked(7)); } } 

2、广度优先搜索

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点。

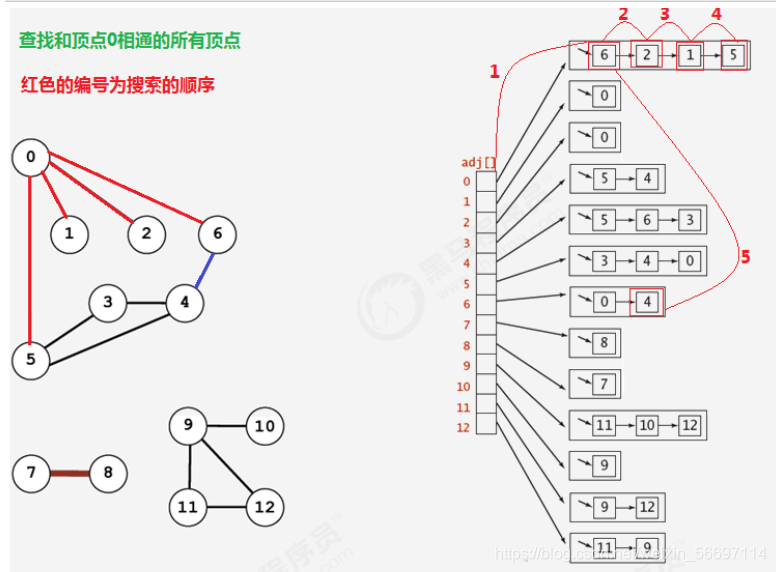
讯享网package graph; import xianxing.Queue; public class BreadthFirstSearch { private boolean[] marked; private int count; //用来存储待搜索邻接表的点 private Queue<Integer> waitSearch; public BreadthFirstSearch(Graph G,int s){ this.marked = new boolean[G.V()]; this.count = 0; this.waitSearch = new Queue<>(); bfs(G,s); } private void bfs(Graph G, int v){ marked[v] = true; waitSearch.enqueue(v); while(!waitSearch.isEmpty()){ Integer wait = waitSearch.dequeue(); for(Object w : G.adj(wait)){ if(!marked[(int)w]){ bfs(G,(int)w); } } } count++; } public boolean marked(int w){ return marked[w]; } public int count(){ return count; } } 

 5、路径查找

在实际生活中，地图是我们经常使用的一种工具，通常我们会用它进行导航，输入一个出发城市，输入一个目的地城市，就可以把路线规划好，而在规划好的这个路线上，会路过很多中间的城市。这类问题翻译成专业问题就是：从s顶点到v顶点是否存在一条路径？如果存在，请找出这条路径。

我们实现路径查找，最基本的操作还是得遍历并搜索图，所以，我们的实现暂且基于深度优先搜索来完成。其搜索的过程是比较简单的。我们添加了edgeTo[]整型数组，这个整型数组会记录从每个顶点回到起点s的路径。

如果我们把顶点设定为0，那么它的搜索可以表示为下图：

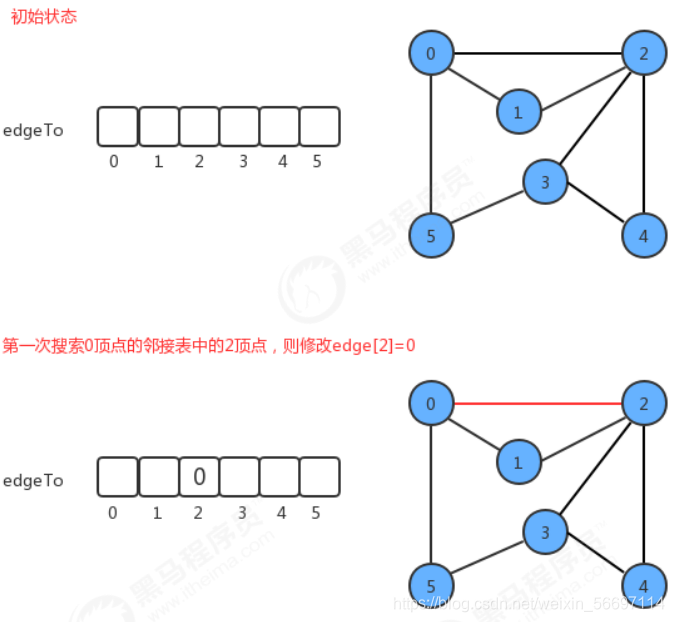
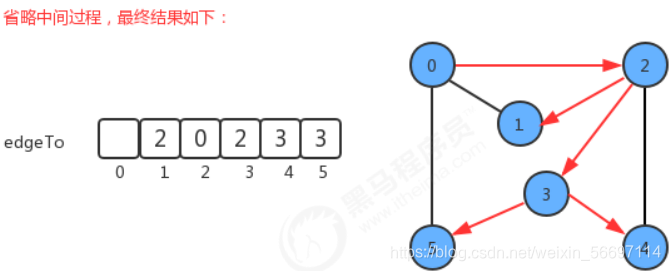
package graph; import xianxing.Stack; public class DepthFirstPaths { private boolean[] marked; //起点 private int s; //索引代表顶点，值代表从起点s到顶点路径上的最后一个顶点 private int[] edgeTo; public DepthFirstPaths(Graph G, int s){ this.marked = new boolean[G.V()]; this.edgeTo = new int[G.V()]; this.s = s; dfs(G,s); } private void dfs(Graph G, int s){ marked[s] = true; for(Object w : G.adj(s)){ if(!marked[(int) w]){ edgeTo[(int) w] = s; dfs(G, (int)w); } } } public boolean hasPathTo(int w){ return marked[w]; } //找出从起点s到顶点v的路径 public Stack<Integer> pathTo(int v){ if(hasPathTo(v)){ return null; } Stack stack = new Stack(); for(int i=v; i!=s;i=edgeTo[i]){ stack.push(i); } stack.push(s); return stack; } }