Friedman 检验--Matlab

大家好，我是讯享网，很高兴认识大家。

一：Friedman检验

Friedman函数（非参数检验）检验矩阵X的各列是否来自于相同的总体，即检验因素A的各水平之间无显著差异，他对分组因素B不感兴趣。Frideman函数返回检验的p值，当检验的p值小于或等于给定的显著性水平时，应拒绝原假设，原假设认为X总体来自于相同的总体。

二：Matlab-- Friedman检验代码

以一个小例子直观表示friedman检验代码应用过程：

例：设有来自A，B，C, D 四个地区的四位名厨制作名菜京城水煮鱼，为了比较它们的品质是否相同，经四位美食评委评分结果如下所示，现利用Friedman检验四位名厨制作的京城水煮鱼这道菜品质有无区别。

	A	B	C	D
评委1	85	82	82	79
评委2	87	75	86	82
评委3	90	81	80	76
评委4	80	75	81	75

假设检验问题为： H_0
讯享网:四个地区的京城水煮鱼品质相同，

H_1 ：四个地区的京城水煮鱼品质不同。

<1>

X=[85,82,82,79; 87,75,86,82; 91,81,80,76; 80,75,81,75] p=friedman(x,regs)

讯享网

X为待检验矩阵，我们的目标是四个地方水煮鱼的品质是否相同。那么同一个评委对四个地区厨师的打分就具有可参考性，而不同地区评委之间对同一个厨师的打分参考性几乎没有。因此，我们认为四个地区是因素A，而评委是因素B（区组因素）。

输出结果如下：

p =

0.0434

p<0.05, 说明在显著性水平0.05下拒绝原假设，则认为这四个地区的有显著性差距。

注：regs为重复实验的次数（行数必须为重复次数的倍数，否则matlab会报错）；

<2>

若想进一步考虑四个地区中哪两个地区具有显著性差别，进一步可以进行如下的检测：

讯享网[p,table,stats]=friedman(x) %返回检验值p值、方差分析表table和结构体变量stats

p =

0.0434

table =

4×6 cell 数组

'Source' 'SS' 'df' 'MS' 'Chi-sq' 'Prob>Chi-sq'
'Columns' [12.8750] [ 3] [4.2917] [8.1316] [ 0.0434]
'Error' [ 6.1250] [ 9] [0.6806] [] []
'Total' [ 19] [15] [] [] []

stats =

包含以下字段的 struct:

source: 'friedman'
n: 4
meanranks: [3.7500 2 2.8750 1.3750]
sigma: 1.2583

%调用multcompare函数进行多重比较 [c,m]=multcompare(stats); c %查看多重比较的结果矩阵c [{'A';'B';'C';'D'},num2cell(m)] %把m矩阵转换为元胞数组，与组名放在一起显示

c =

1.0000 2.0000 -0.5358 1.7500 4.0358 0.2006
1.0000 3.0000 -1.4108 0.8750 3.1608 0.7589
1.0000 4.0000 0.0892 2.3750 4.6608 0.0381
2.0000 3.0000 -3.1608 -0.8750 1.4108 0.7589
2.0000 4.0000 -1.6608 0.6250 2.9108 0.8962
3.0000 4.0000 -0.7858 1.5000 3.7858 0.3311

ans =

4×3 cell 数组

'A' [3.7500] [0.6292]
'B' [ 2] [0.6292]
'C' [2.8750] [0.6292]
'D' [1.3750] [0.6292]

从以上结果可以看出，c矩阵的第3行的第3列和第5列构成的区间不包括0，说明在显著性水平0.05下，可认为A，D两个地区制作的水煮鱼这道菜的品质之间的差异是显著的。进一步可以通过MATLAB生成的Friedman 检验图直观的看出：

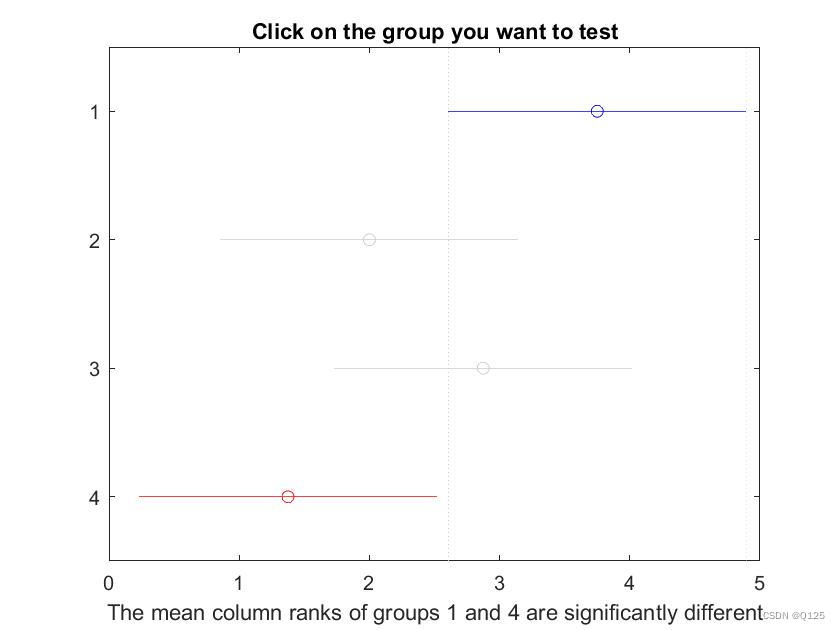
如上图所示，横轴是平均序值，纵轴是每个算法、对于每一个算法，用一个圆点显示其平均序值，以圆点为中心的横线段表示临界值域的大小。观察图，若两个算法的横线段有交叠，说明两个算法没有显著的差别。由图可以看出，A与D有明显差距。

三：Friedman检验用于检验算法

Friedman检验可以用于检验某一指标下，对多个算法在多个数据集的性能进行比较。

相关推荐