1.矩阵特征值和特征向量定义
A为n阶矩阵,若数λ和n维非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量。式Ax=λx也可写成( A-λE)x=0,并且|λE-A|叫做A 的特征多项式。当特征多项式等于0的时候,称为A的特征方程,特征方程是一个齐次线性方程组,求解特征值的过程其实就是求解特征方程的解。
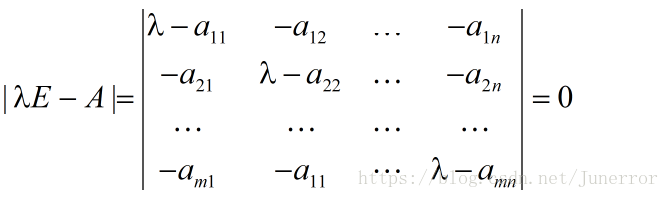
计算:A的特征值和特征向量。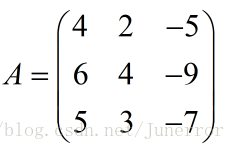
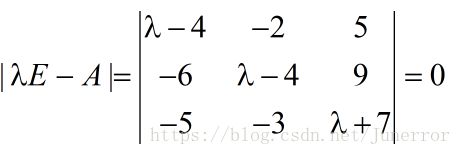
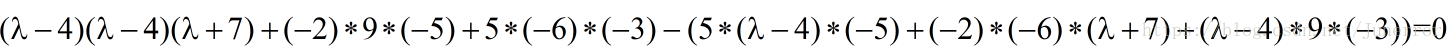
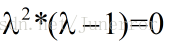
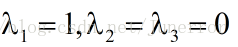
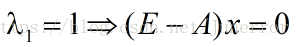
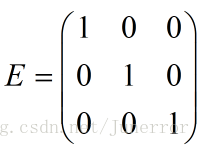
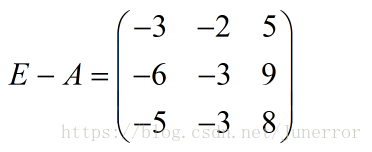 化简得:
化简得: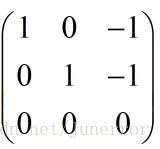
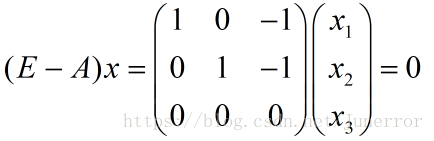
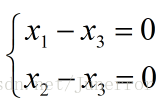

令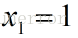 得到特征矩阵:
得到特征矩阵:
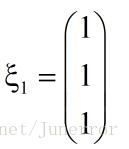
同理,当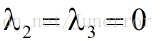 得:
得:
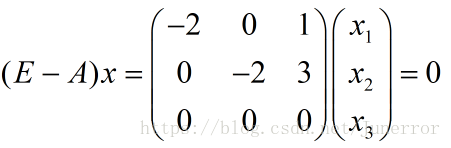 ,
,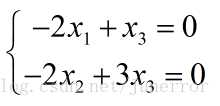
令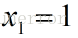 得到特征矩阵:
得到特征矩阵:
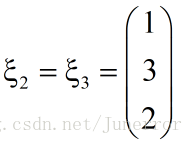
矩阵特征值和特征向量详细计算过程1 矩阵特征值和特征向量定义 A 为 n 阶矩阵 若数 和 n 维非 0 列向量 x 满足 Ax x 那么数 称为 A 的特征值 x 称为 A 的对应于特征值 的特征向量 式 Ax x 也可写成 A E x 0 并且 E A 叫做 A 的特征多项式 当特征多项式等于 0 的时候 称为 A 的特征方程
A为n阶矩阵,若数λ和n维非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量。式Ax=λx也可写成( A-λE)x=0,并且|λE-A|叫做A 的特征多项式。当特征多项式等于0的时候,称为A的特征方程,特征方程是一个齐次线性方程组,求解特征值的过程其实就是求解特征方程的解。
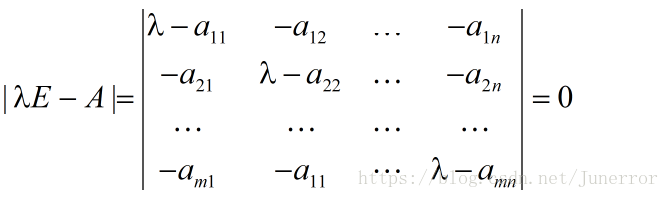
计算:A的特征值和特征向量。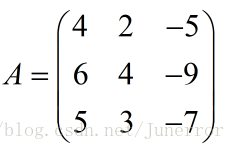
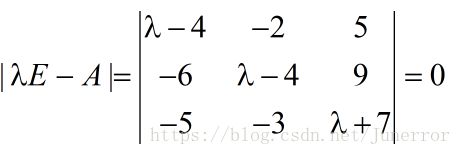
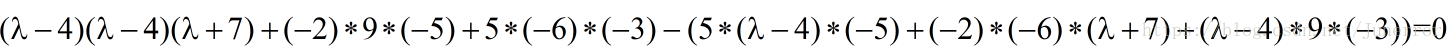
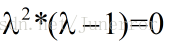
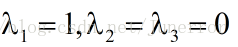
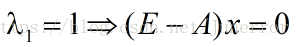
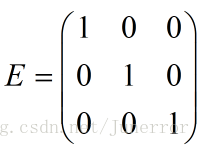
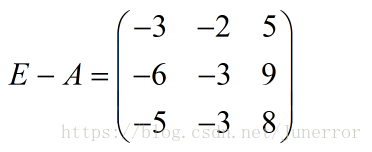 化简得:
化简得: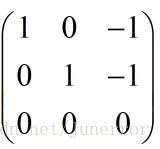
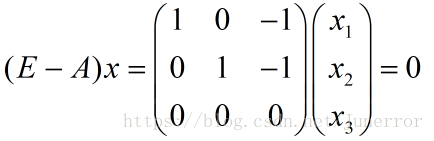
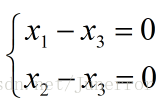

令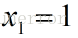 得到特征矩阵:
得到特征矩阵:
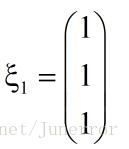
同理,当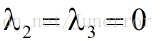 得:
得:
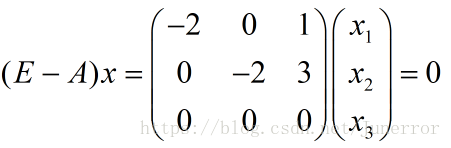 ,
,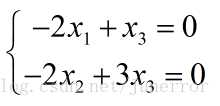
令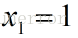 得到特征矩阵:
得到特征矩阵:
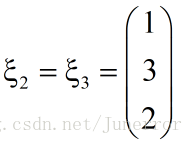
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/27409.html