tensorboard ckpt pb 模型的输出节点_乐学初中数学研究-第七期：最值问题之费马点模型...

大家好，我是讯享网，很高兴认识大家。

熊俐老师

讯享网

同济大学硕士毕业；以数学第一及总分第一考入研究生；具有较强的逻辑思维能力，解题方法独特；从研究生开始就从事初中数学教学辅导工作；熟悉初中教材，能准确把握教学重点难点，教学风格细致

最值问题之费马点模型

人类每天为解决最大最小问题而忙碌着，大自然亦是如此。最早指出自然界中到处都潜藏着最大最小问题的人，大概是费马。

Q：Who is 费马？

费马(1601-1665)，1601年8月30日出生于法国南部卢兹，他在大学里学的是法律，后来的全职工作是律师，并把几乎全部业余时间用于数学研究。然而，在17世纪的法国还找不到哪位数学家可以与之匹敌：他是解析几何的发明人之一；对于微积分诞生的贡献仅次于牛顿、莱布尼茨，概率论的主要创始人，以及独承17世纪数论天地的人，成为17世纪最著名的数学家之一，人称“业余数学家之王”。

Q：What is 费马点？

在已知∆ABC所在平面上求一点P，使它到三角形三顶点的距离之和为最小。

这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，这个问题中所求的点被人们称为“费马点”。

值得一提的是这个特殊点对于每个给定的三角形都只有一个。

Q：Where is 费马点？

三角形的费马点分为两种情况：

1、若三角形的三个内角均小于120°，那么费马点与三角形三个顶点连线所构成的夹角均为120°

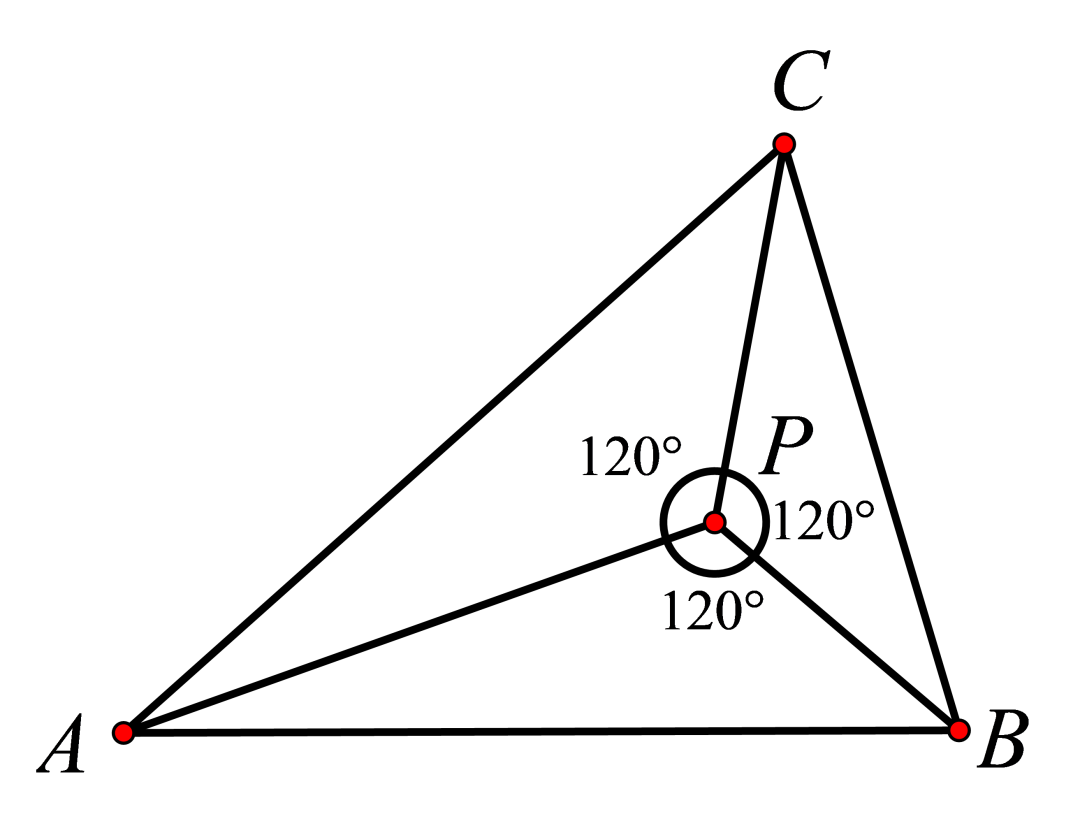
2、若三角形有一内角大于或等于120°，则此钝角的顶点就是距离和最小的点(费马点)

Q：How to find 费马点？

首先我们来看第一种情况：

当三角形三个内角均小于120°时。

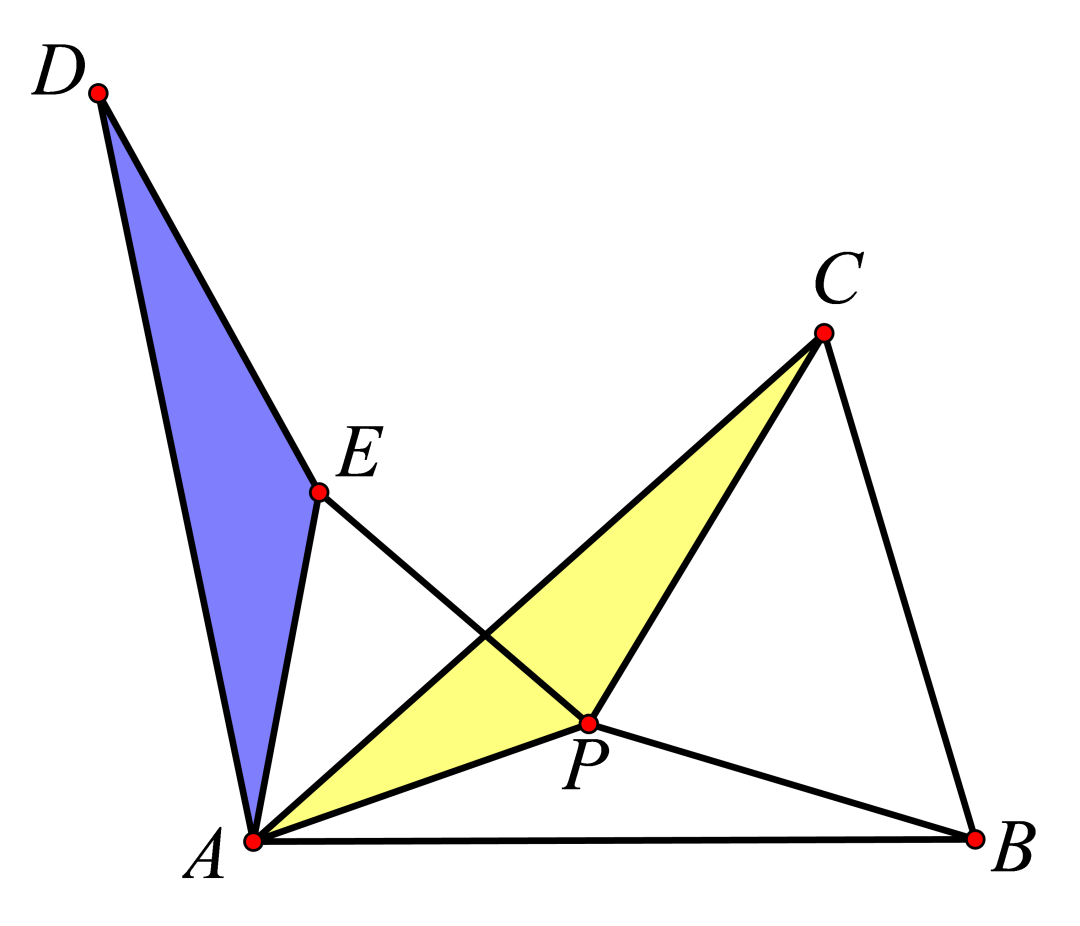
假设∆ABC内有任意一点P，此时PA+PB+PC并不是最小的，因此我们要找到费马点！任取∆ABC的一个顶点A，以A为旋转中心，将∆ACP逆时针旋转60°到∆ADE位置，这样就通过旋转构造了全等三角形和一个等边三角形AEP。

易知PA=PE，PC=ED，因此PA+PB+PC的长就等于DE+EP+PB，显然当D、E、P、B四点共线时，距离之和最短。所以当E、P、B共线时，∠APB=120°；而当D、E、P共线时，∠AED=∠APC=120°，所以点P应该与三个顶点的连线所构成的夹角均为120°，这就是费马点的位置。

接下来我们再看第二种情况：

若三角形有一内角大于或等于120°时。

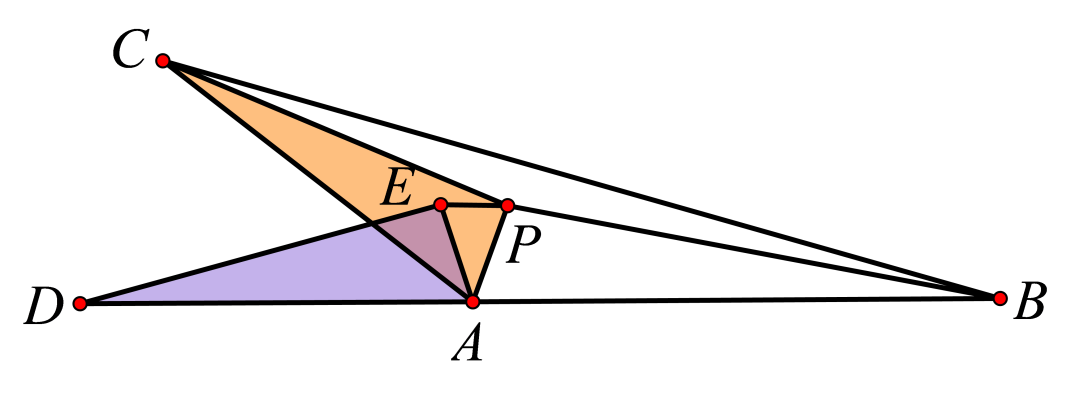
在∆ABC内任取一点P，然后绕点A逆时针旋转∆ACP使得D、A、B三点共线。

∴∆ADE≌∆ACP,AE=AP

∵∠BAC≥120°

∴∠EAP=180°-∠BAP-∠DAE

=180°-∠BAP-∠CAP

=180°-∠BAC

≤60°

∴AP≥EP(大角对大边)

∴AP+PB+PC≥EP+PB+DE＞BD=AB+AC

∴A是费马点

Q：还有没有其他找法？

如图，以∆ABC的三边为边，分别向外作等边三角形BCD、ACE、ABF，连接AD、BE、CF，则有结论：

(1)AD、BE、CF交于一点P，且∠APB=∠APC=∠BPC=120°；

(2)P到A、B、C三顶点距离的和最小，且PA+PB+PC=AD=BE=CF。

这样去做等边三角形之后再连接，其实也就是手拉手模型，那么我们来简单证明一下：

(1)证明：由手拉手模型易证∆AFC≌∆ABE

∴CE=BE

同理可证：∆BCF≌∆BDA,CF=AD

∴AD=BE=CF

∵∆AFC≌∆ABE

∴∠AFC=∠ABE

∴∠BPF=∠BAF=60°(8字模型)

∴∠BPC=120°

同理可证：∠APB=∠APC=120°

∴∠APB=∠APC=∠BPC=120°

(2)证明并不困难，给一点小提示：在FC上取一点Q，使得FQ=AP，接下来的证明过程就交给各位同学自行完成了

Q：你学会了吗？

让我们来考验一下各位小学霸吧！

【例1】如图，菱形ABCD的对角线AC上有一动点P，BC=6，∠ABC=150°，求AP+BP+PD的最小值。

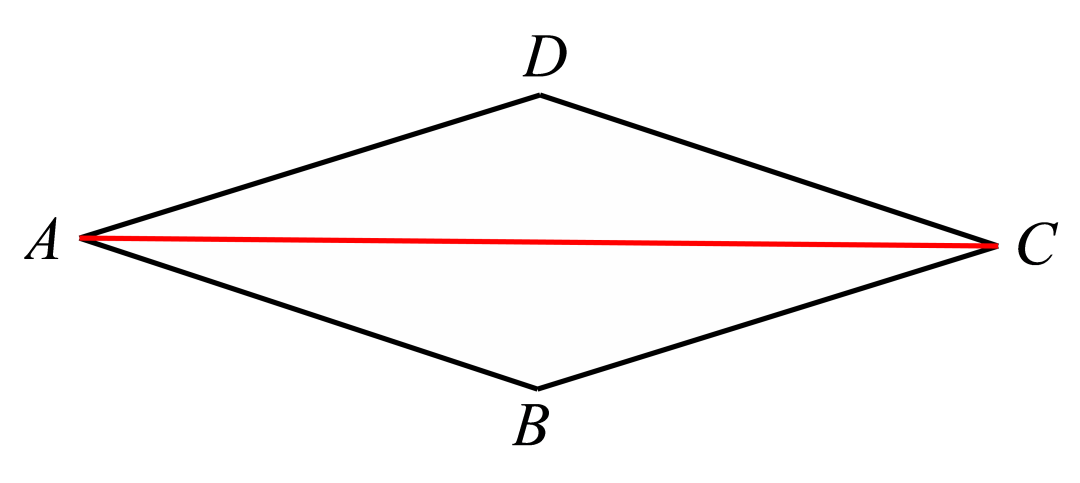
【分析】首先很容易知道△ABD是一个等腰三角形，所以它的费马点肯定在AC这条线段上，然后题目让我们求的最小值，其实就是问费马点到三个顶点的距离之和。

根据前面的方法和总结，我们可以以AB为边往外做一个等边三角形。

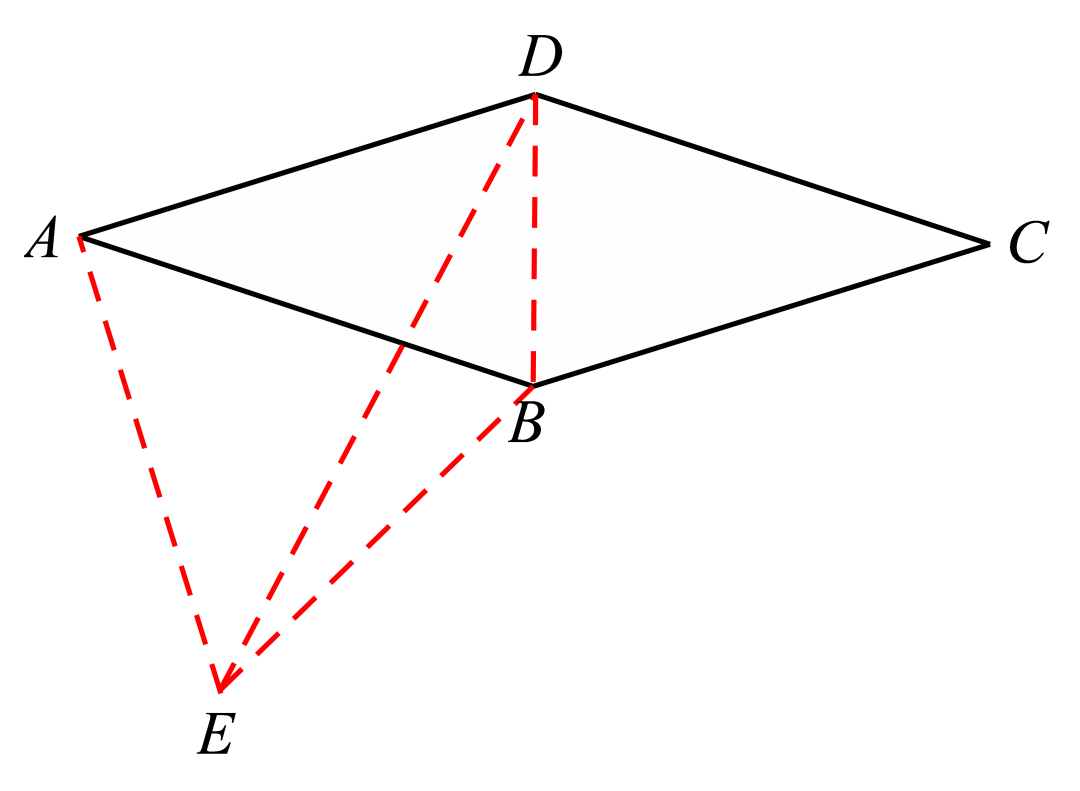
所以前面的结论很快就知道AP+BP+PD=DE。而由题干给出的角度条件，很容易就得出∆ADE是一个等腰直角三角形，所以DE就很容易求出来了。

接下来看看中考真题吧！

【例2】(2016年株洲中考)已知P是∆ABC内一点，且它到三角形的三个定点距离之和最小，则P叫∆ABC的费马点(Fermat point)。

已经证明：在三个内角均小于120°的∆ABC中，当∠APB=∠APC=∠BPC=120°时，P就是的费马点。若点P是腰长为√2的等腰Rt∆DEF的费马点，则PD+PE+PF=__________。

【分析】此题没有给出图形，而且对费马点原理做出了提示，所以题目貌似并不超出考试大纲的要求，但是如果考生平时对费马点知识掌握不牢固，要想快速解出该题答案也是有难度的，实际上该题只要能把图做出来，找到费马点在哪里，基本上离答案不远了。

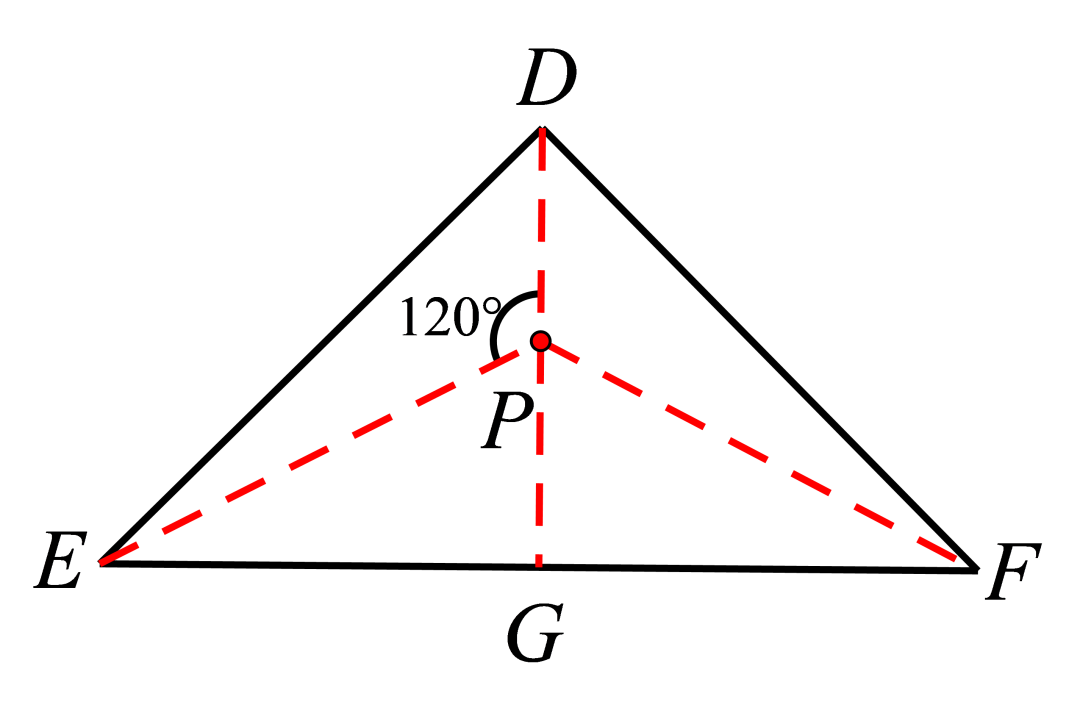
小结：可以看出，只要知道费马点的位置，问题就转换成勾股定理的相关计算，此题对费马点原理的提示是比较清晰，有些考题可能就不是这样，它更多的以探究题的形式出现，难度就会增加很多，比如下面武汉2019年中考题的一道填空压轴题。

【例3】(2019年武汉中考填空压轴)问题背景：如图1，将∆ABC绕点A逆时针旋转60°得到∆ADE，DE与BC交于点P，可推出结论：PA+PC=PE。

问题解决：如图2，在∆MNG中，MN=6，∠M=75°，MG=4√2。点O是∆MNG内一点，则点O到∆MNG三个顶点的距离之和的最小值是__________。

【分析】此题没有提到费马点，但它的确是一道费马知识的问题。如果你平时不熟悉费马点，可能都意识不到问题背景给你的提示有什么用。而且，此题的问题背景，P点并不在三角形内部，和费马点的辅助线思路还是有一些区别，尽管他们都是旋转60°的思路。繁殖，如果考生知道本题求O点到三角形三个定点的最小值，就意味着O是费马点，这样，按照费马点的位置特点，就比较容易做出该题了。

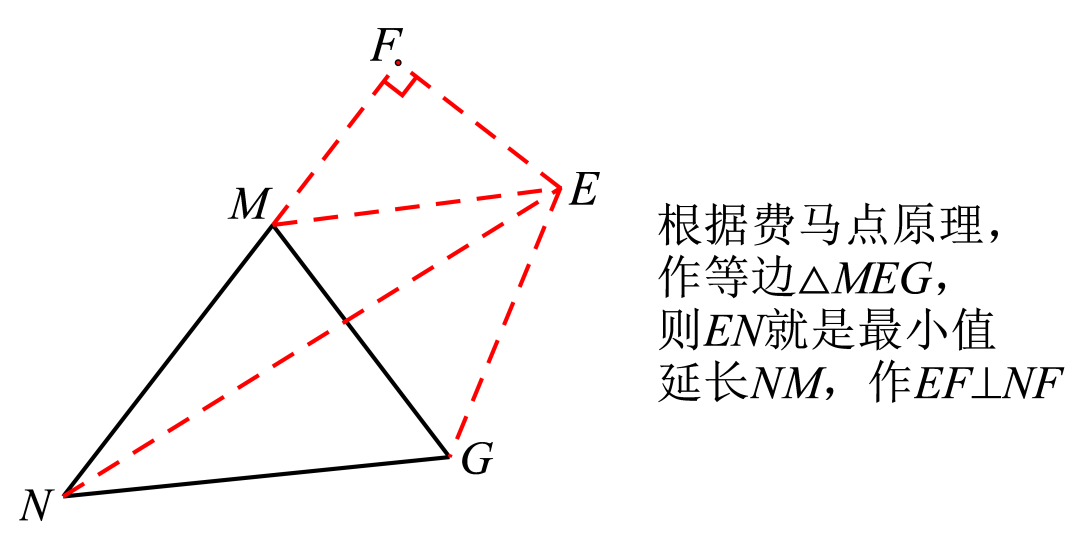
根据条件易得∠NME=135°，这是一个非常特殊的角度，所以很容易想到∠EMF=45°。而∆MGE是等边三角形，所以ME=MG=4√2，所以计算出EM=EF=4。所以NF=10，再由勾股定理即可算出NE=2√29。

Q：最后还想说点啥？

中考是选拔性考试，总是要出一些稍微有难度的题目，把优秀的学生筛选出来，把他们送进高中的学堂。所以，现在的教材虽然剔除了一些看似比较难的知识点，但这并不代表这些知识点就不会出现在中考题中，它会以探究题、创新题等形式出现。所以这些知识点，我们仍然要引起重视，在平时的学习中加以总结、提炼，才能在决定命运的考场上立于不败之地。

我们在数学学习过程中，是否需要“模型”？俗话说“成也模型，败也模型”，我们掌握一定的模式，能让我们快速找到解决问题的途径。如果死守模式，不会融会贯通，也是“假模式”。我们平时教学中的每一道典型例题都是一种模型，取一个好听的名字知识让学生好记，能“顾名思义”。求线段和最值问题，不管是“将军饮马”问题、“胡不归”问题、“阿式圆”问题，及“费马点”问题，本质都是将直线拉直(将直线同一侧的两条线段转化为异侧)，再利用“两点之间线段最短”或“垂线段最短”寻找到答案。