5.2  参数调整和调试优化

在实际应用中，通过调整和调试PID控制器的参数，可以确保系统获得良好性能。通常，PID参数的调整和调试工作需要一些试错和经验。在本节的内容中，将详细讲解PID参数的调整和调试的常见方法和技巧。

5.2.1  手动调整法

"手动调整法"是指在调整PID（比例-积分-微分）控制器的参数时，工程师通过手动试验、观察和调整的方法来优化系统性能。这种方法通常包括逐步调整比例增益 Kp、积分时间 Ti和微分时间 Td这三个参数，以找到**的参数组合，使系统能够在不产生过度振荡或失稳的情况下快速而稳定地响应。

1. 比例增益 Kp：从零开始逐渐增加，直到系统开始出现振荡。比例增益Kp负责根据当前误差的大小提供控制输出，逐渐增加Kp会使系统对误差更敏感，从而引起振荡。逐步减小Kp直到振荡减小，找到合适的比例增益，既能快速响应系统，又能保持稳定。
2. 积分时间Ti：逐渐增加Ti，观察系统的响应速度和稳定性。确保系统没有积分饱和，即积分项不会使系统过度响应。这样可以提高系统的稳定性和抗干扰能力。需要确保增大Ti后系统仍能快速稳定。
3. 微分时间Td：逐渐增加Td，观察系统的抑制振荡和稳定性。确保微分项不会引入额外的噪音或导致系统不稳定。然而，过大的Td可能会引入噪音，导致系统不稳定。因此，在调整Td时需要注意平衡抑制振荡和稳定性之间的关系。

例如在机器人领域中，可以考虑一个简单的轮式移动机器人的速度控制问题。下面是一个使用PID控制算法进行手动调整的例子，机器人的目标是维持在速度为5的目标速度。通过手动调整Kp、Ki和Kd参数，可以观察到系统的响应变化，以及调整这些参数对系统性能的影响。请注意，在实际应用中可能需要更复杂的模型和参数调整方法。

实例5-1：在机器人应用中调整PID控制器的参数（源码路径：codes\5\pid\shou.py）

实例文件shou.py的具体实现代码如下所示。

import simpy import matplotlib.pyplot as plt class Robot: def __init__(self, env, Kp, Ki, Kd): self.env = env self.speed = 0 # 初始速度 self.target_speed = 5 # 目标速度 self.error = 0 self.last_error = 0 self.Kp = Kp self.Ki = Ki self.Kd = Kd self.speed_data = [] def update_speed(self): while True: # 计算PID控制输出 proportional = self.Kp * self.error integral = self.Ki * sum(self.speed_data) derivative = self.Kd * (self.error - self.last_error) control_output = proportional + integral + derivative # 限制控制输出在合理范围内 control_output = max(min(control_output, 10), -10) # 更新速度 self.speed += control_output # 记录速度数据，用于积分项计算 self.speed_data.append(self.speed) # 计算误差 self.error = self.target_speed - self.speed # 记录上一次的误差 self.last_error = self.error # 等待一段时间，模拟控制周期 yield self.env.timeout(0.1) def simulate(self, runtime): env.process(self.update_speed()) self.env.run(until=runtime) # 手动调整PID参数 Kp = 1.0 Ki = 0.1 Kd = 0.01 # 创建仿真环境和机器人对象 env = simpy.Environment() robot = Robot(env, Kp, Ki, Kd) # 运行仿真，模拟10秒钟的时间 robot.simulate(10) # 绘制速度曲线 plt.plot(robot.speed_data) plt.xlabel('Time (s)') plt.ylabel('Speed') plt.title('PID Control Simulation') plt.show()

上述代码的实现流程如下所示：

1. 首先，定义了类Robot表示机器人，其中包含机器人的速度、目标速度、误差、以及PID控制的参数（Kp、Ki、Kd）。
2. 接着，通过SimPy创建了仿真环境和机器人对象。在机器人对象中实现了update_speed方法，该方法通过PID控制算法计算控制输出，更新机器人的速度，并模拟控制周期。
3. 然后，调用simulate方法运行仿真，模拟了一定时间范围内的机器人速度控制过程。
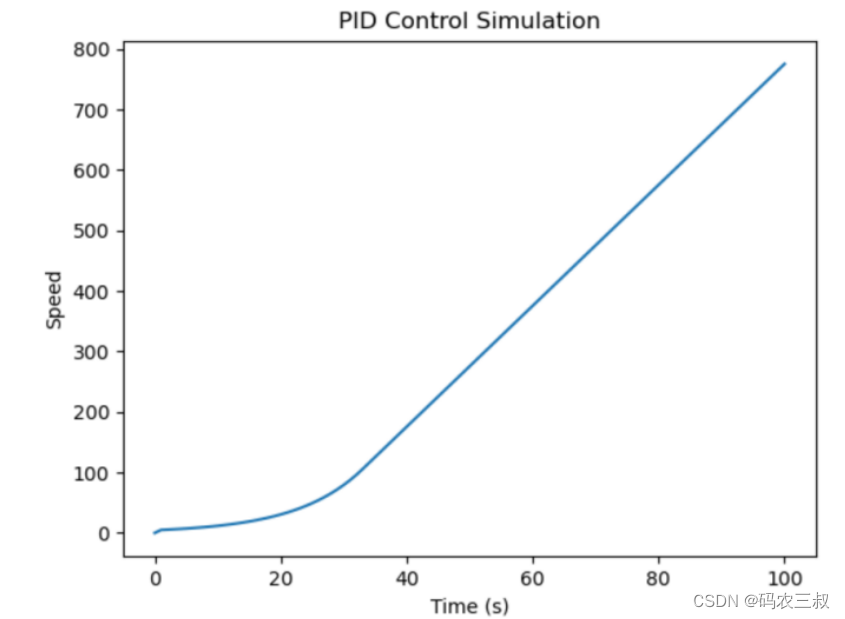
4. 最后，利用Matplotlib库绘制了PID控制下的速度曲线，使用户能够观察和分析手动调整PID参数对系统响应的影响。效果如图5-1所示。

讯享网

图5-1  速度变化曲线图

5.2.2  Ziegler-Nichols方法

Ziegler-Nichols方法是一种用于调整PID控制器参数的经验性方法，最初由John G. Ziegler和Nathaniel B. Nichols于1942年提出。Ziegler-Nichols方法通过分析系统的阶跃响应曲线来确定合适的PID参数，具体实现步骤如下所示。

（1）设置 Ki和 Kd为零： 将积分项 Ki和微分项 Kd设置为零，只保留比例项Kp。

（2）逐渐增加 Kp：从零开始逐渐增加比例增益 Kp，直到系统出现持续的振荡（周期性的输出波动）。

（3）确定临界增益 Kpc和周期Tpc：记录持续振荡时的比例增益 Kpc和振荡周期 Tpc，这是系统的临界增益和临界周期。

（4）计算 Ki和 Kd：Ki可以通过以下公式计算：Ki=0.5⋅Kpc/Tpc 

Kd可以通过以下公式计算：

Kd=0.125⋅Kpc⋅Tpc

（5）调整 Kp, Ki, Kd：根据实际需要，可以进一步调整 Kp , K i , K d的值。

Ziegler-Nichols方法主要适用于一阶或二阶系统，对于高阶系统可能不够精确。此方法的优势在于其简单性和直观性，但使用时需要小心，因为在实际系统中可能引入不稳定性。一些自动化工具箱或软件工具（如MATLAB/Simulink的工具箱）也提供Ziegler-Nichols自动调整算法，可帮助更方便地进行参数调整。

例如在智能驾驶领域中，经常需要控制车辆的纵向速度。下面是一个使用Ziegler-Nichols方法进行PID控制的例子，将车辆的目标是维持在速度为20的目标速度。通过Ziegler-Nichols方法确定参数Kp、Ki和 Kd的初始值。然后，通过SimPy进行仿真，观察在PID控制下的车辆速度响应。

实例5-2：使用Ziegler-Nichol方法控制车辆的速度（源码路径：codes\5\pid\zn.py）

实例文件zn.py的具体实现代码如下所示。

讯享网import simpy import matplotlib.pyplot as plt class Vehicle: def __init__(self, env, Kp, Ki, Kd): self.env = env self.velocity = 0 self.target_velocity = 20 # 目标速度 self.error = 0 self.last_error = 0 self.Kp = Kp self.Ki = Ki self.Kd = Kd self.velocity_data = [] def update_velocity(self): while True: # 计算PID控制输出 proportional = self.Kp * self.error integral = self.Ki * sum(self.velocity_data) derivative = self.Kd * (self.error - self.last_error) control_output = proportional + integral + derivative # 限制控制输出在合理范围内 control_output = max(min(control_output, 5), -5) # 更新速度 self.velocity += control_output # 记录速度数据，用于积分项计算 self.velocity_data.append(self.velocity) # 计算误差 self.error = self.target_velocity - self.velocity # 记录上一次的误差 self.last_error = self.error # 等待一段时间，模拟控制周期 yield self.env.timeout(0.1) def simulate(self, runtime): env.process(self.update_velocity()) self.env.run(until=runtime) # 使用Ziegler-Nichols方法确定PID参数 Kp = 0.6 Ki = 0.5 Kd = 0.075 # 创建仿真环境和车辆对象 env = simpy.Environment() vehicle = Vehicle(env, Kp, Ki, Kd) # 运行仿真，模拟20秒钟的时间 vehicle.simulate(20) # 绘制速度曲线 plt.plot(vehicle.velocity_data) plt.xlabel('Time (s)') plt.ylabel('Velocity') plt.title('PID Control Simulation using Ziegler-Nichols Method') plt.show()

上述代码的实现流程如下所示：

1. 首先，定义了一个名为Vehicle的类，表示具有PID控制的车辆模型。在初始化时，分别设置了初始速度、目标速度和PID控制的参数Kp、Ki和Kd。
2. 接着，定义了update_velocity方法，使用PID控制算法来更新车辆的速度。在这个方法中，计算了比例、积分和微分项，然后通过限制控制输出的范围来更新车辆的速度。整个过程中，我们记录了速度数据和误差项，模拟了控制周期。
3. 接着，通过simulate方法将update_velocity方法加入仿真环境中，并运行仿真直至指定的运行时间。
4. 最后，我们使用Ziegler-Nichols方法确定了初始的Kp、Ki和Kd参数的值，创建了仿真环境和车辆对象，并运行了20秒钟的仿真。最终，通过Matplotlib库绘制了车辆速度随时间变化的曲线，用于观察PID控制在Ziegler-Nichols方法下的性能。效果如图5-1所示。

图5-1  车辆速度变化曲线图

5.2.3  频率响应法

频率响应法是一种用于调整PID控制器参数的方法，通过分析系统对不同频率输入的响应来确定**的参数值。频率响应法基于系统对不同频率信号的响应，通过分析系统的幅频特性和相频特性来调整PID参数。这种方法常用于线性时不变系统，其中系统的频率响应可以用传递函数或系统函数来表示。

1. 实现步骤

实现频率响应法的基本步骤如下所示。

（1）生成频率扫描信号：在频率响应法中，通常使用正弦波信号作为输入信号。通过改变正弦波信号的频率，我们可以观察系统对不同频率的响应。

（2）测量系统的幅频特性和相频特性：将正弦波信号输入系统，测量系统对应频率下的输出幅值和相位。这样可以得到系统的频率响应曲线。

（3）分析曲线：观察系统的频率响应曲线，找到系统的截止频率、相位裕度等关键特性。这些特性反映了系统对不同频率的响应情况。

（4）调整PID参数：根据频率响应曲线的分析结果，调整PID参数，以使系统的频率响应更符合性能要求。通常需要平衡系统的稳定性、响应速度和抗干扰能力。

2. 参数调整

1. 比例增益 Kp：调整比例增益可以影响系统的整体增益，直接影响系统对高频信号的响应。
2. 积分时间 Ti：调整积分时间可以影响系统对低频信号的响应，提高系统的稳定性。
3. 微分时间 Td：调整微分时间可以影响系统对高频信号的相位，改善系统的相位裕度。

3. 软件工具和模拟

使用工具如MATLAB/Simulink中的频率响应分析工具箱，可以更方便地进行频率响应分析和参数调整。通过仿真模拟，可以在不同频率下测试系统响应，加速参数调整过程。

总体而言，频率响应法是一种有效的PID参数调整方法。频率响应法提供了一种直观而全面的分析方式，能够更准确地调整PID参数以适应系统的频率特性，适用于需要考虑系统动态特性和频率响应的控制系统。在使用频率响应法时，需要考虑系统的稳定性、相位裕度和幅值裕度，以确保系统在各个频率范围内都具有良好的性能。

例如在下面的例子中，将机器人的维持在速度为5的目标速度。通过使用频率响应法，在simulate方法中传递了频率参数，以模拟不同频率下的系统响应。通过观察速度曲线，可以更直观地了解系统在不同频率下的行为，从而更好地调整PID参数以满足性能要求。

实例5-3：使用频率响应法控制机器人的速度（源码路径：codes\5\pid\pin.py）

实例文件pin.py的具体实现代码如下所示。

import simpy import matplotlib.pyplot as plt import numpy as np class Robot: def __init__(self, env, Kp, Ki, Kd): self.env = env self.velocity = 0 self.target_velocity = 5 # 目标速度 self.error = 0 self.last_error = 0 self.Kp = Kp self.Ki = Ki self.Kd = Kd self.velocity_data = [] def update_velocity(self, frequency): while True: # 生成频率扫描信号（正弦波信号）和相位变化 input_signal = np.sin(2 * np.pi * frequency * self.env.now) phase_variation = np.sin(2 * np.pi * frequency * 0.5 * self.env.now) # 引入相位变化 # 计算PID控制输出 proportional = self.Kp * self.error integral = self.Ki * sum(self.velocity_data) derivative = self.Kd * (self.error - self.last_error) control_output = proportional + integral + derivative # 限制控制输出在合理范围内 control_output = max(min(control_output, 5), -5) # 更新速度，将输入信号和相位变化都添加到速度中 self.velocity += control_output + input_signal + 0.5 * phase_variation # 记录速度数据，用于积分项计算 self.velocity_data.append(self.velocity) # 计算误差 self.error = self.target_velocity - self.velocity # 记录上一次的误差 self.last_error = self.error # 等待一段时间，模拟控制周期 yield self.env.timeout(1.0 / frequency) def simulate(self, runtime, frequency): env = self.env # 将env定义在simulate方法中 env.process(self.update_velocity(frequency)) env.run(until=runtime) # 生成频率响应法的例子 def frequency_response_example(): # 频率扫描范围 frequencies = np.arange(0.1, 2.0, 0.1) # 存储结果 amplitude_response = [] phase_response = [] for frequency in frequencies: # 创建仿真环境和机器人对象 env = simpy.Environment() robot = Robot(env, 0.6, 0.5, 0.075) # 运行仿真，模拟10秒钟的时间 robot.simulate(10, frequency) # 记录幅频特性和相频特性 amplitude_response.append(max(robot.velocity_data)) phase_response.append(np.angle(robot.velocity_data[-1], deg=True)) # 绘制频率响应曲线 plt.figure(figsize=(12, 5)) plt.subplot(1, 2, 1) plt.plot(frequencies, amplitude_response) plt.xlabel('Frequency (Hz)') plt.ylabel('Amplitude Response') plt.title('Frequency Response - Amplitude') plt.subplot(1, 2, 2) plt.plot(frequencies, phase_response) plt.xlabel('Frequency (Hz)') plt.ylabel('Phase Response (degrees)') plt.title('Frequency Response - Phase') plt.tight_layout() plt.show() # 执行例子 frequency_response_example()

在上述代码中，生成了一个频率扫描信号，即正弦波信号，并将其添加到速度中。通过在不同频率下运行仿真，记录了机器人系统的幅频特性和相频特性。最后，通过绘制频率响应曲线，可以观察系统对不同频率的响应情况。上述代码的实现流程如下所示：

1. 首先，创建了一个名为Robot的类，用于模拟机器人的速度控制系统。该类包含了初始化方法__init__，其中定义了机器人的初始状态，包括速度、目标速度和PID控制器的参数。同时，定义了update_velocity方法，该方法在仿真过程中计算机器人的速度响应，引入了频率扫描信号和相位变化。还实现了simulate方法，该方法用于运行整个仿真过程。
2. 其次，编写了名为frequency_response_example的函数，该函数演示了频率响应法的应用。在函数中，首先定义了频率扫描范围，并创建了存储结果的空列表。然后，通过迭代不同的频率，创建了仿真环境和机器人对象，运行仿真过程并记录幅频特性和相频特性。最后，绘制了两个子图，一个显示幅频特性，另一个显示相频特性。
3. 最后，执行frequency_response_example函数，可视化展示了整个频率响应法的仿真过程，如图5-2所示。在可视化图形，左侧子图展示了幅频特性的变化，右侧子图展示了相频特性的变化。

图5-2  幅频特性和相频特性的模拟图

注意：上面的第二个子图是水平直线，可能是因为幅值较小或者引入的随机性不够明显。我们可以尝试使用更大的随机成分phase_variation或者调整其他参数，以确保相位变化在仿真过程中更加明显。

注意：在进行PID参数调整时，请遵循如下所示的建议。

1. 逐步调整：一次只调整一个参数，以避免引入不稳定性。
2. 记录数据：记录每次调整的结果，以便比较和回溯。
3. 注意系统限制：确保调整后的参数在实际系统中是可行和合理的。
4. 考虑鲁棒性：调整参数时，考虑系统可能面临的不确定性和变化。

PID参数的调整通常需要一些实践和经验，因此，在实际应用中可能需要多次试验和调整，以找到**的参数组合。