本文来介绍拓朴排序的基本内容~

AOV网络

AOV网（activity on vertex network）本质上是有向图，表示一个有一定规模的“工程”。图中的顶点表示工程中的不同活动，图中的边表示各项活动之间的先后顺序关系（制约关系）。

拓扑序列

有向图G=(V，E)具有 n 个顶点，从顶点 vi到 vj 有一条路径，顶点序列 v0, v1, …, vn-1中顶点 vi 必在顶点 vj 之前，此时的顶点序列 v0, v1, …, vn-1 称为一个拓扑序列。显然，这个序列可以让网中所有存在的前驱和后继关系都能得到满足！

显然，拓扑序列用以描述AOV网络，AOV网络中一定不存在回路！反之，无回路的有向图一定可以输出拓扑序列！

拓朴排序

构造拓扑序列的过程称为拓扑排序。

由上文可知，拓朴序列正确的前提是图中无回路，因此，拓朴排序可以用来检测有向图中是否存在回路！！

算法实现

拓朴排序的过程简言之，就是从源点出发，按边（制约关系）依次输出顶点，并删除已找到的点和边（制约关系)

基本思路

循环以下步骤，直到输出全部顶点，或AOV网中不存在没有前驱的顶点：

• 从AOV网中选择一个没有前驱的顶点并且输出；
• 从AOV网中删去该顶点，并删去所有从该顶点出发的边；

那如何表示前驱顶点呢？接下来介绍拓朴排序算法的存储结构！

存储结构

由于需要在图中找到顶点间的连接关系，因此该算法中图使用邻接表存储。

结构体声明：

讯享网

struct EdgeNode //邻接边表结点 { int adjvex; //邻接点域 EdgeNode *next; //指向邻接表的指针 }; 

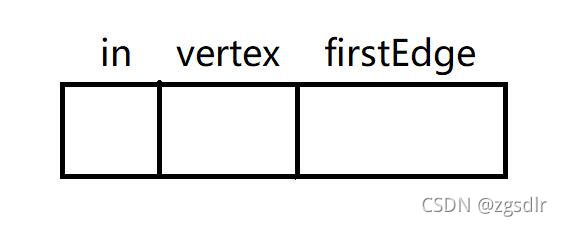
1. 为表示顶点前驱结点的有无，在顶点表中，增加“入度域”。

   
   结构体声明：

   讯享网struct VertexNode //顶点表结点 { int in; //入度域 DataType vertex; //顶点数据 EdgeNode *firstEdge; //指向邻接表的指针 }; 

2. 为查找没有前驱的顶点，使用栈（或队列）临时存储入度为0的点，并通过出栈（或出队）对栈顶（或队首）指向的顶点遍历其邻接表。

总之，拓扑排序算法的存储结构为：用带入度的邻接表、顶点表表示图，用栈存放入度为0且未被输出的顶点！

代码实现

该算法仍然用C++面向对象的方法实现功能：

类的声明

class ALGraph { public: ALGraph(DataType a[ ], int n, int e); //构造n个顶点e条边的图 ~ALGraph( ); //析构函数，释放邻接表各边表结点的存储空间 void TopSort( ); private: VertexNode adjlist[MaxSize]; //存放顶点表的数组 int vertexNum, edgeNum; //图的顶点数和边数 }; 

构造

与邻接表存储有向图的构造函数类似，思路不再复述。

唯一不同之处是增加了入度域，因此在构造时需要存入各顶点的入度信息！！

简言之，拓扑排序建图构造函数要完成的工作为：
1.存储顶点信息到顶点表；
2.存边权信息到邻接表 ；
3.存入度信息到入度域。

讯享网ALGraph :: ALGraph(DataType a[ ], int n, int e) { int i, j, k; EdgeNode *s = nullptr; vertexNum = n; edgeNum = e; for (i = 0; i < vertexNum; i++) //输入顶点信息，初始化顶点表 { adjlist[i].vertex = a[i]; adjlist[i].firstEdge = NULL; } for (k = 0; k < edgeNum; k++) //依次输入每一条边 { cout << "输入边所依附的两个顶点的编号："; cin >> i >> j; //输入边所依附的两个顶点的编号 s = new EdgeNode; s->adjvex = j; //生成一个边表结点s s->next = adjlist[i].firstEdge; //将结点s插入到第i个边表的表头 adjlist[i].firstEdge = s; } for (i = 0; i < vertexNum; i++) { cout << "依次输入每个顶点的入度："; cin >> adjlist[i].in; } } 

析构

与邻接矩阵不同，邻接表使用了动态存储，需要手动析构！！

ALGraph :: ~ALGraph( ) { EdgeNode *p = NULL, *q = NULL; //工作指针p ，临时指针q（暂存被删除元素） for (int i = 0; i < vertexNum; i++) { p = q = adjlist[i].firstEdge; //工作指针p用于向后移动 ；临时指针q暂存被删元素 while (p != NULL) { p = p->next; delete q; q = p; } } } 

核心代码

首先，将入度为0的顶点入栈；之后，取栈顶结点，输出栈顶结点信息后对其邻接点依次遍历完成删边并找入度为0的点压栈的操作。对栈的操作直到栈空为止！

讯享网void ALGraph :: TopSort( ) { int i, j, k, count = 0; //i操作顶点；j、k为临时变量；count记录已输出的结点数 int S[MaxSize], top = -1; //顺序栈初始化 EdgeNode *p = nullptr; for (i = 0; i < vertexNum; i++) //顶点表中，无前驱结点的顶点下标压栈 if (adjlist[i].in == 0) S[++top] = i; //入度为0的顶点入栈 while (top != -1 ) //当栈中有入度为0的顶点时 { //取栈顶元素，输出并记数 j = S[top--]; //从栈中取出入度为0的顶点 cout << adjlist[j].vertex << "\t"; count++; //对栈顶元素的邻接点操作:删边、查入度、压栈 p = adjlist[j].firstEdge; //工作指针p初始化 while (p != nullptr) //扫描顶点表，找出顶点j的所有出边 { k = p->adjvex; adjlist[k].in--; //修改入度完成删边！ if (adjlist[k].in == 0) S[++top] = k; //将入度为0的顶点入栈 p = p->next; } } if (count < vertexNum ) cout << "有回路"; //拓扑序列中，各顶点仅出现一次，最终输出点的数量与顶点数相同。若顶点数与输出数量不一致，证明图中存在回路！ } 

测试程序

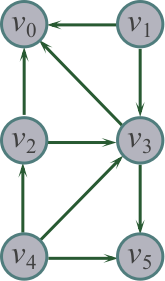
顶点名称为字符型.

主函数部分代码：

 char ch[ ] = {'A','B','C','D','E','F'}; int i; ALGraph ALG(ch, 6, 9); ALG.TopSort();