讯享网
记得在设置里面开原始影像尺寸哦
都支持的。这个链接可以很好的回答,老外写得很简单,不明白机翻一下即可
《为什么你的图像不使用420色度抽样?》这里也提到的subsample子采样
JPEG压缩原理简介和PhotoShop保存JPG子采样分析Photoshop不允许用户选择是否在JPEG压缩中使用色度二次采样。取而代之的是,将2x2子采样用于质量6及以下的所有“另存为” ,而将其禁用(即1x1子采样)用于质量7及更高的“另存为” 。同样,它用于质量为50或更低的所有Save For Web操作,而质量为51或更高的Save for Web不使用 。
你好,电脑上看是图很清楚,出图不清楚,这是常见的情况,PS做图工具选项中设置JPEG的图片质量,品质选项设置为**。祝你工作顺利。
您好,您可以在菜单栏选项点击——图像——图像大小——提高分辨率(或者缩小图片尺寸)
保存jpg是有损压缩的格式,体积比较小。
看你的用途,如果对分辨率有要求,建议更改分辨率,压缩比,或者存储为无损格式。
通常情况下不会传播木马病毒。木马病毒主要依赖于恶意代码的存在和执行才能感染其他设备或系统。只是简单地将照片和聊天记录从受感染设备复制到新的设备,不会复制或传播木马病毒。
但是,如果你同时将受感染设备中的其他文件或应用程序复制到新设备上,那么可能会传播木马病毒。因此,在迁移文件和应用程序时,建议使用可信任的渠道和方式,确保不会将感染的文件或应用程序复制到新设备上。
此外,为了确保新设备的安全,建议在迁移后对新设备进行全面的安全扫描,以检测和清除任何潜在的木马病毒或恶意代码。
JPEG的全称是JointPhotographicExpertsGroup(联合图像专家小组),它是一种常用的图像存储格式, jpg/jpeg是24位的图像文件格式,也是一种高效率的压缩格式,文件格式是JPEG(联合图像专家组)标准的产物,该图像压缩标准是国际电信联盟(International Telecommunication Union,ITU)、国际标准化组织(International Organization for Standardization,ISO)和国际电工委员会(International Electrotechnical Commission,IEC)共同制定。JPEG标准正式地称为ISO/IEC IS(国际标准)10918-1:连续色调静态图像数字压缩和编码(Digital Compression and Coding of Continuous-tone Still Images)和ITU-T建议T.81。
JPEG是第一个国际图像压缩标准,用于连续色调静态图像(即包括灰度图像和彩色图像),其最初目的是使用64Kbps的通信线路传输720×576 分辨率压缩后的图像。通过损失极少的分辨率,可以将图像所需存储量减少至原大小的10%。由于其高效的压缩效率和标准化要求,目前已广泛用于彩色传真、静止图像、电话会议、印刷及新闻图片的传送上。但那些被删除的资料无法在解压时还原,所以* .jpg/.jpeg文件并不适合放大观看,输出成印刷品时品质也会受到影响。
JPEG的文件格式一般有两种文件扩展名:.jpg和.jpeg,这两种扩展名的实质是相同的,我们可以把.jpg的文件改名为.jpeg,而对文件本身不会有任何影响。严格来讲,JPEG的文件扩展名应该为.jpeg,由于DOS时代的8.3文件名命名原则,就使用了.jpg的扩展名,这种情况类似于.htm和.html的区别。
JPEG标准不指定任何固有的文件格式。它只定义压缩比特流的语法。这就产生了一定数量的文件格式来存储JPEG压缩后的图像,例如JPEG文件交换格式(JPEG File Interchange Format,JFIF),JPEG推广到TIFF6.0、FlashPix等。但它们中的每一个都不能认为是由国际标准委员会支持的正式定义的国际标准。
JPEG格式可以分为标准JPEG、渐进式JPEG和JPEG2000三种格式。
标准JPEG:该类型的图片文件,在网络上应用较多,只有图片完全被加载和读取完毕之后,才能看到图片的全貌;它是一种很灵活的图片压缩方式,用户可以在压缩比和图片品质之间进行权衡。不过,通常来讲,其压缩比在10:1到40:1之间,压缩比越大,品质就越差,压缩比越小,品质就越好。JPEG格式压缩的主要是高频信息,对色彩的信息保留较好,适合应用于互联网,可减少图像的传输时间,可以支持24bit真彩色,也普遍应用于需要连续色调的图像。JPEG由于可以提供有损压缩,因此压缩比可以达到其他传统压缩算法无法比拟的程度。其压缩模式有以下几种:
- 顺序式编码(SequentialEncoding)
- 递增式编码(ProgressiveEncoding)
- 无失真编码(LosslessEncoding)
- 阶梯式编码(HierarchicalEncoding)
- 颜色转换:由于JPEG只支持YUV颜色模式,而不支持RGB颜色模式,所以在将彩色图像进行压缩之前,必须先对颜色模式进据转换。转换完成之后还需要进行数据采样。一般采用的采样比例是2:1:1或4:2:2。由于在执行了此项工作之后,每两行数据只保留一行,因此,采样后图像数据量将压缩为原来的一半。
- DCT变换:DCT(DiscreteConsineTransform)是将图像信号在频率域上进行变换,分离出高频和低频信息的处理过程。然后再对图像的高频部分(即图像细节)进行压缩,以达到压缩图像数据的目的。首先将图像划分为多个8*8的矩阵。然后对每一个矩阵作DCT变换(变换公式此略)。变换后得到一个频率系数矩阵,其中的频率系数都是浮点数。
- 量化:由于在后面编码过程中使用的码本都是整数,因此需要对变换后的频率系数进行量化,将之转换为整数。由于进行数据量化后,矩阵中的数据都是近似值,和原始图像数据之间有了差异,这一差异是造成图像压缩后失真的主要原因。
- 编码:编码采用两种机制:一是0值的行程长度编码;二是熵编码(EntropyCoding)。在JPEG中,采用曲徊序列,即以矩阵对角线的法线方向作“之”字排列矩阵中的元素。这样做的优点是使得靠近矩阵左上角、值比较大的元素排列在行程的前面,而行程的后面所排列的矩阵元素基本上为0值。行程长度编码是非常简单和常用的编码方式,在此不再赘述。编码实际上是一种基于统计特性的编码方法。在JPEG中允许采用HUFFMAN编码或者算术编码。
更详细可以参看《色彩空间RGB/CMYK/HSL/HSB/HSV/Lab/YUV基础理论及转换方法:RGB与YUV》、《视频采样,量化,编码,压缩,解码相关技术原理学习笔记 》
Baseline JPEG/基本JPEG:这种类型的JPEG文件存储方式是按从上到下的扫描方式,把每一行顺序的保存在JPEG文件中。打开这个文件显示它的内容时,数据将按照存储时的顺序从上到下一行一行的被显示出来,直到所有的数据都被读完,就完成了整张图片的显示。这种图片在web中,如果没有给图片指定宽高,会造成重绘。
progressive jpeg/渐进式JPEG:JPEG文件包含多次扫描,这些扫描顺寻的存储在JPEG文件中。打开文件过程中,会先显示整个图片的模糊轮廓,随着扫描次数的增加,图片变得越来越清晰。该类型的图片是对标准JPEG格式的改进,当在网页上下载渐进式JPEG图片时,首先呈现图片的大概外貌,然后再逐渐呈现具体的细节部分,因而被称之为渐进式JPEG。这种通过HTTP2 多路复用传递渐进式JPEG的扫描图层来提高感知性能和速度指数的方式已经早在2012年被Google的John Mellor 注意到了。他一直在实验SPDY协议,HTTP2的前身。
JPEG2000:一种全新的图片压缩发,压缩品质更好,并且改善了无线传输时,因信号不稳定而造成的马赛克及位置错乱等问题。另外,作为JPEG的升级版,JPEG2000的压缩率比标准JPEG高约30%,同时支持有损压缩和无损压缩。它还支持渐进式传输,即,先传输图片的粗略轮廓,然后,逐步传输细节数据,使得图片由模糊到清晰逐步显示。此外,JPEG2000还支持感兴趣区域,也就是说,可以指定图片上感兴趣区域的压缩质量,还可以选择指定的部分先进行解压。还有个优势就是,JPEG2000从无损压缩到有损压缩可以兼容
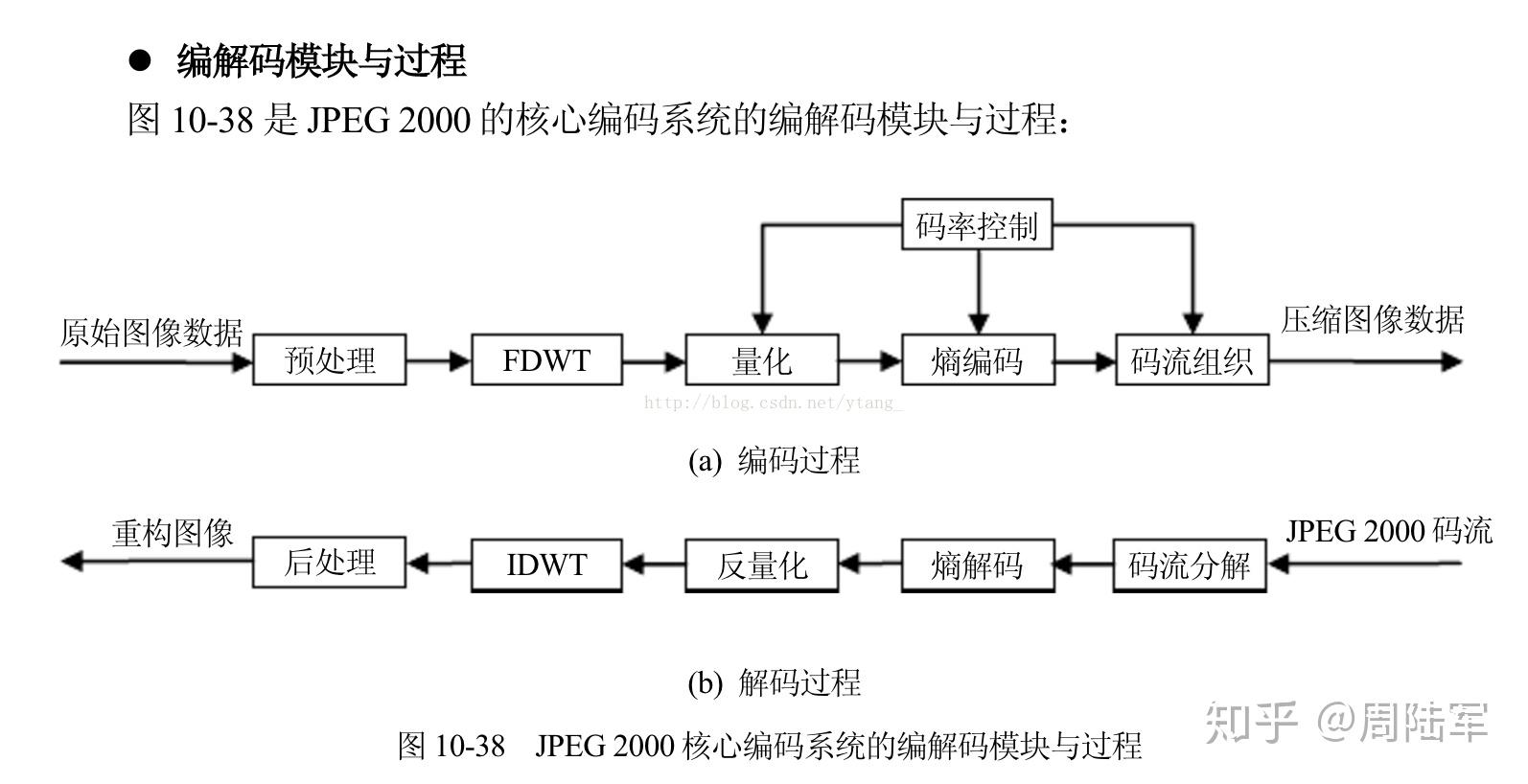
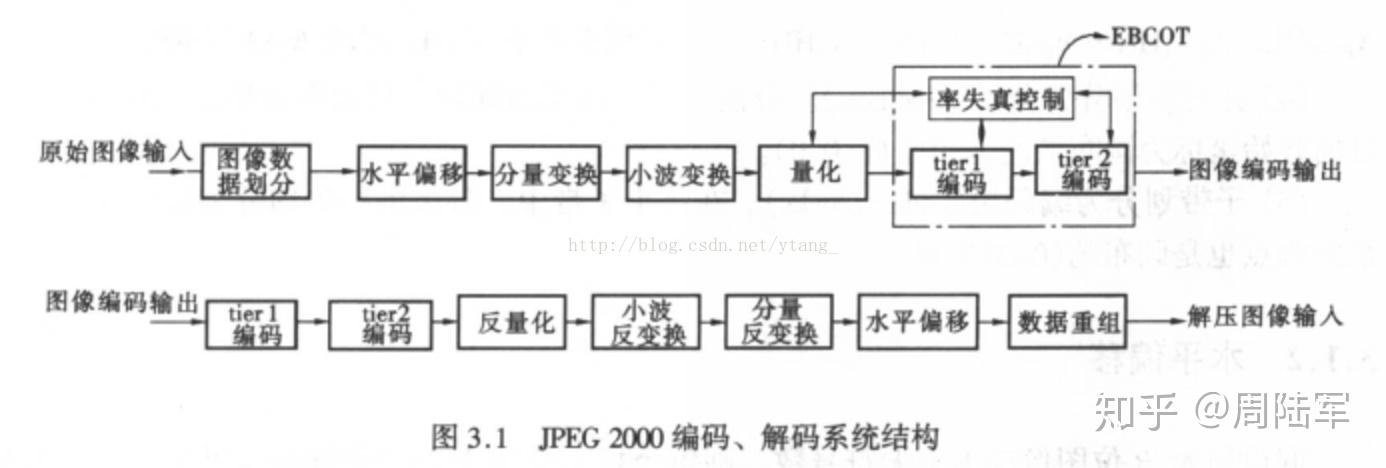
由于JPEG的有损压缩方式(Lossy mode of operation)并不比其他的压缩方法更优秀,
因此我们着重来看它的有损压缩中最常用的基线JPEG算法(baseline sequential)。以一幅24位彩色图像为例,JPEG的压缩步骤分为:
JPEG支持图像采用任何一个色彩空间,支持1~4个颜色分量。灰度图像颜色分量数为1。RGB、YUV、YCbCr等拥有3种颜色分量。4种颜色分量的例子是青、洋红、黄和黑(Cyan,Magenta,Yellow,and Black,CMYK)。为了减少色度通道包含的大量的冗余信息,本例中采用YCbCr色彩空间。首先需要进行从RGB到YCbCr的色彩空间变换:
- Y = 0.R + 0.G + 0.B
- Cb = -0.R - 0.G + 0.B
- Cr = 0.R - 0.G - 0.081312B
其中,Y表示亮度分量,Cb和Cr表示蓝红色度分量。
最初,在图像中的像素存储在无符号的整数中。对于数学计算,在图像中任何变换或数学计算开始之前,根本上是将这些采样转换成两个补码表示。DC电平偏移的目的是保证输入图像的采样有近似地集中在零附近的动态范围。DC电平偏移执行的图像采样只通过无符号数表示。
方法:假设图片分量的采样精度为n,那么分量中的每个像素值应减去2的(n-1)次幂。
对于图像而言他的采样由无符号的整数表示,例如CT(X光断层成像)图像,动态范围已经集中于零附近,所以不需要DC电平偏移。
DCT(DiscreteCosineTransform)是将图像信号在频率域上进行变换,分离出高频和低频信息的处理过程。然后再对图像的高频部分(即图像细节)进行压缩,以达到压缩图像数据的目的。首先将图像划分为多个8*8的矩阵。然后对每一个矩阵作DCT变换。变换后得到一个频率系数矩阵,其中的频率系数都是浮点数。
由于在后面编码过程中使用的码本都是整数,因此需要对变换后的频率系数进行量化,将之转换为整数。由于进行数据量化后,矩阵中的数据都是近似值,和原始图像数据之间有了差异,这一差异是造成图像压缩后失真的主要原因。
编码采用两种机制:一是0值的行程长度编码;二是熵编码(EntropyCoding)。
在JPEG中,采用曲徊序列,即以矩阵对角线的法线方向作“之”字排列矩阵中的元素。这样做的优点是使得靠近矩阵左上角、值比较大的元素排列在行程的前面,而行程的后面所排列的矩阵元素基本上为0值。
- 行程长度编码是非常简单和常用的编码方式,在此不再赘述。
需要注意的是,AC系数的之字形序列编码中有两个特殊符号——(0,0)和(15,0)。第一个特殊符号指的是块的结束(end-of-block,EOB),用来表明在之字形块中剩余的元素都是零。另一个特殊符号是指零游程长度(zero-run-length,ZRL),用来表明16个零游程。基线JPEG允许的零游程最大长度是16个。如果这里的零超过16个,那么这个游程分成几个长度为16的零游程。 - 使用DPCM对直流系数(DC)进行编码
DCT系数量化之后,通过差分编码对量化后的DC系数编码。当前块的DC系数减去前个块的DC系数,然后对其差值进行编码,如右图所示。这就利用了邻接块DC值之间的空间相关性。 - 熵编码:编码实际上是一种基于统计特性的编码方法。在JPEG中允许采用HUFFMAN编码或者算术编码。而基线JPEG算法(baseline sequential)采用的是前者。
经过RLE编码的AC系数可以映射成两个标志(RUNLENGTH,CATEGORY)和(AMPLITUDE),前者采用的是霍夫曼编码,而后者采用的是VLI编码。同理经过DPCM编码的DC系数同样可以映射成两个标志(CATEGORY)和(AMPLITUDE),前者采用霍夫曼编码,后者采用VLI编码。
基线JPEG允许使用4个霍夫曼表,两个用于AC系数编码,两个用于DC系数编码。
其实很简单,就是判断前面3个字节是什么,如果发现是FF D8 FF开始,那就认为它是JEPG图片。
JPG文件是由一段段的数据构成的组成的(segment),段的多少和长度并不是一定的。只要包含了足够的信息,该JPEG文件就能够被打开。
JPEG图片格式组成部分:SOI(文件头)+APP0(图像识别信息)+ DQT(定义量化表)+ SOF0(图像基本信息)+ DHT(定义Huffman表) + DRI(定义重新开始间隔)+ SOS(扫描行开始)+ EOI(文件尾)
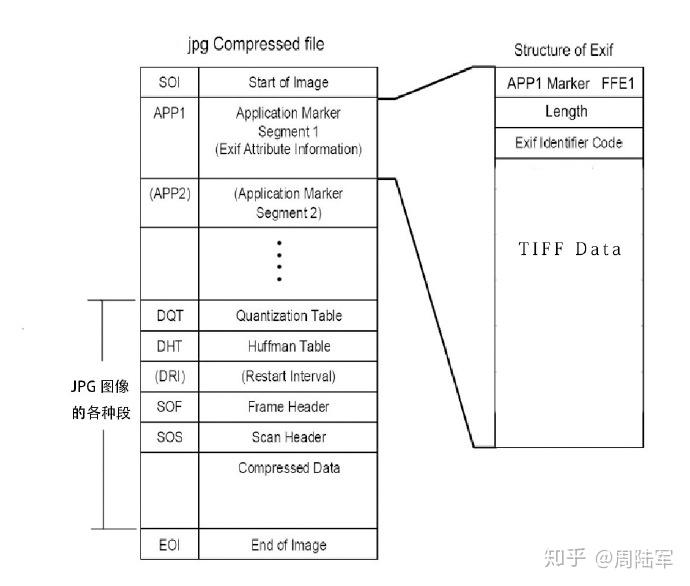
以16进制模式打开JPG文件,就会发现
JPEG 文件中有一些形如 0xFF 这样的数据,它们被称为“标志(Marker)”,它表示 JPEG 信息数据段。例如 0xFFD8 代表 SOI(Start of image), 0xFFD9 代表 EOI(End of image)。
标志 0xFFE0~0xFFEF 被称为 “Application Marker”,它们不是解码 JPEG 文件必须的,可以被用来存储配置信息等。EXIF 也是利用这个标志段来插入信息的,具体来说,是 APP1(0xFFE1) Marker。所有的 EXIF 信息都存储在该数据段。
名称 标记码 说明
SOI D8 文件头 EOI D9 文件尾 SOF0 C0 帧开始(标准 JPEG) SOF1 C1 同上 DHT C4 定义 Huffman 表(霍夫曼表) SOS DA 扫描行开始 DQT DB 定义量化表 DRI DD 定义重新开始间隔 APP0 E0 定义交换格式和图像识别信息 DNL DC 标记码 COM FE 注释
段类型有30种,但只有10种是必须被所有程序识别的,其它的类型都可以忽略。
SOI MarkerMarker XX size=SSSSMarker YY size=TTTTSOS Marker size=UUUUImage streamEOI MarkerFFD8FFXXSSSSDDDD……FFYYTTTTDDDD……FFDAUUUUDDDD….I I I I….FFD9
Exif也使用应用标记来插入数据, 但是Exif 使用 APP1(0xFFE1)标记来避免与JFIF格式的 冲突. 且每一个 Exif 文件格式都开始于它, 如
SOI 标记标记 XX 的大小=SSSS标记 YY 的大小=TTTTSOS 标记 的大小=UUUU图像数据流EOI 标记FFD8FFXXlo0pSSSSDDDD……FFYYTTTTDDDD……FFDAUUUUDDDD….I I I I….FFD9
Exif也使用应用标记来插入数据, 但是Exif 使用 APP1(0xFFE1)标记来避免与JFIF格式的 冲突. 且每一个 Exif 文件格式都开始于它, 如;
0xFF+Marker Number(1 byte)+Data size(2 bytes)+Data(n bytes)
SOI MarkerAPP1 MarkerAPP1 DataOther MarkerFFD8FFE1SSSS 0 TTTT……FFXX SSSS DDDD……
该图像文件从SOI(0xFFD8) 标记开始, 因此它是一个 JPEG 文件. 后面马上跟着 APP1 标记. 而它的所有 Exif数据都被存储在 APP1 数据域中. 上面的 “SSSS” 这部分表示 APP1 数据域 (Exif data area)的大小. 请注意这里的大小 “SSSS” 包含描述符本身的大小.
在 APP1 标记域的后面是, 跟随着其他的 JPEG 标记
如果图片图片是16进制数据,如下:
FF D8 FF E0 00 10 4A 46 49 46 00 01 02 01 00 60 00 60 00 00 FF E1 08 32 45 78 69 66 00 00 49 49 10 60 00 60 20 00 …… FFD9
那么FF D8为SOI标志位,FF E0为exif文件起始位,后面四位 为exif marker信息的长度。取这个长度的数据解析为TIFFdata数据,exif直接解析为字符串貌似也没有问题。
FF D8
FF E0 00 10 4A 46 49 46 00 01 02 01 00 60 00 60 00 00 mark0,00 10 =16位
FF E1 08 32 45 78 69 66 00 00 49 49 10 60 00 60 20 00 …… mark1,00 10 =2098位
……
Image stream
FFD9
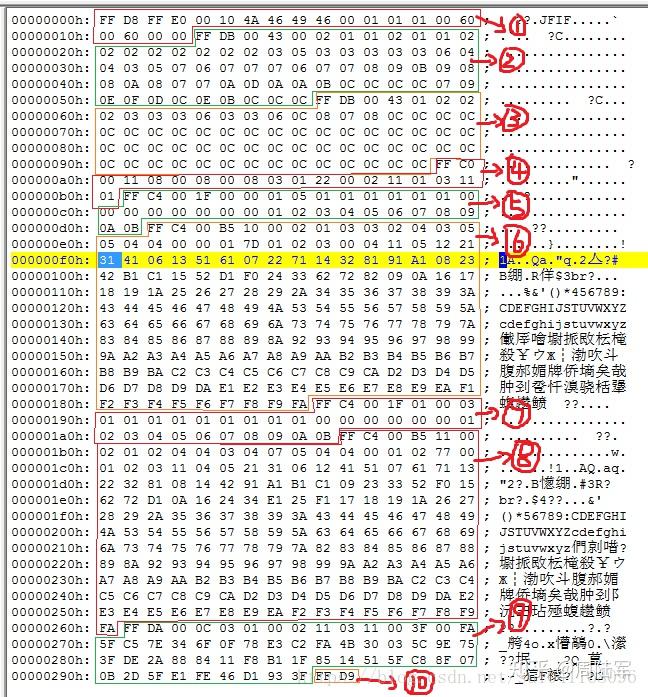
每个段都是由FFxx开头,其中xx是段的标识,接着就是就是两位的端长度。后面跟着的就是数据。前面的元数据外读取完成后,后面的二进制数据就是图片数据。
数据大小描述符(2个字节) 是 “Motorola” 的字节顺序, 数据的低位被存放在高地址,也就是 BigEndian. 请注意上面中的 “数据内容” 中包含他前面的数据大小描述符, 如果下面的是一个标记的话;
这个长度的表示方法是按照高位在前,低位在后的,与 Intel 的表示方法不同。比方说一个段的长度是0x12AB,那么它会按照0x12,0xAB的顺序存储。但是如果按照Intel的方式:高位在后,低位在前的方式会存储成0xAB,0x12,而这样的存储方法对于JPEG是不对的。这样的话如果一个程序不认识JPEG文件某个段,它就可以读取后两个字节,得到这个段的长度,并跳过忽略它。
关于exif信息解码,请阅读《JPEG/Exif/TIFF格式解读(2):图片元数据保存及EXIF详解》
讯享网————————————————-
名称 字节数 值 说明
名称 字节数 值 说明
段标识 1 FF 段类型 1 DB 段长度 2 43 其值=3+n(当只有一个QT时) (以下为段内容) QT信息 1 0-3位:QT号 4-7位:QT精度(0=8bit,1字节;否则=16bit,2字节) QT n n=64×QT精度的字节数
说明:
- JPEG文件一般有2个DQT段,为Y值(亮度)定义1个, 为C值(色度)定义1个。
- 一个DQT段可以包含多个QT, 每个都有自己的信息字节
参考资料:
图片文件Exif信息详细说明 http://blog.sina.com.cn/s/blog_651251e60102uz3d.html#AboutExif
图像Exif信息 元数据(Metadata) https://www.jianshu.com/p/a6d67df60e7e
关于图片文件旋转JPEG与EXIF信息 https://blog.csdn.net/yulimin/article/details/
https://www.media.mit.edu/pia/Research/deepview/exif.html
https://baike.baidu.com/item/Exif/?fr=aladdin
读取JPG图片的Exif属性(一) - Exif信息简介 https://blog.csdn.net/fioletfly/article/details/
读取JPG图片的Exif属性(二) - C代码实现 https://blog.csdn.net/fioletfly/article/details/
读取JPG图片的Exif属性(三) - Exif属性读取GPS信息代码(C/C++实现)https://blog.csdn.net/fioletfly/article/details/
在jpg图片添加Exif信息的C程序实现 https://blog.csdn.net/psy6653/article/details/
JPEG添加EXIF https://blog.csdn.net/weixin_43/article/details/
jpeg图片格式详解 https://blog.csdn.net/yunhen/article/details/
压缩算法——JPEG2000 编解码原理 https://blog.csdn.net/ytang/article/details/
PNG、JPEG、BMP等几种图片格式详解 https://www.jianshu.com/p/f5557c0e689e
使用HTTP2和渐进式JPEG图片更快的加载图像 https://www.zcfy.cc/article/performance-calendar-raquo-even-faster-images-using-http2-and-progressive-jpegs-2216.html
转载本站文章《JPEG/Exif/TIFF格式解读(1):JEPG图片压缩与存储原理分析》,
请注明出处:https://www.zhoulujun.cn/html/theory/multimedia/CG-CV-IP/8396.html
一、各考点确认时间汇总今年由于疫情的原因,很多考点都改为了网上确认。
但是值得我们注意的是很多考点的线上(现场)确认时间和省(市)网报公告要求的确认时间不一致,我们先来看看各省(市)的现场确认时间:
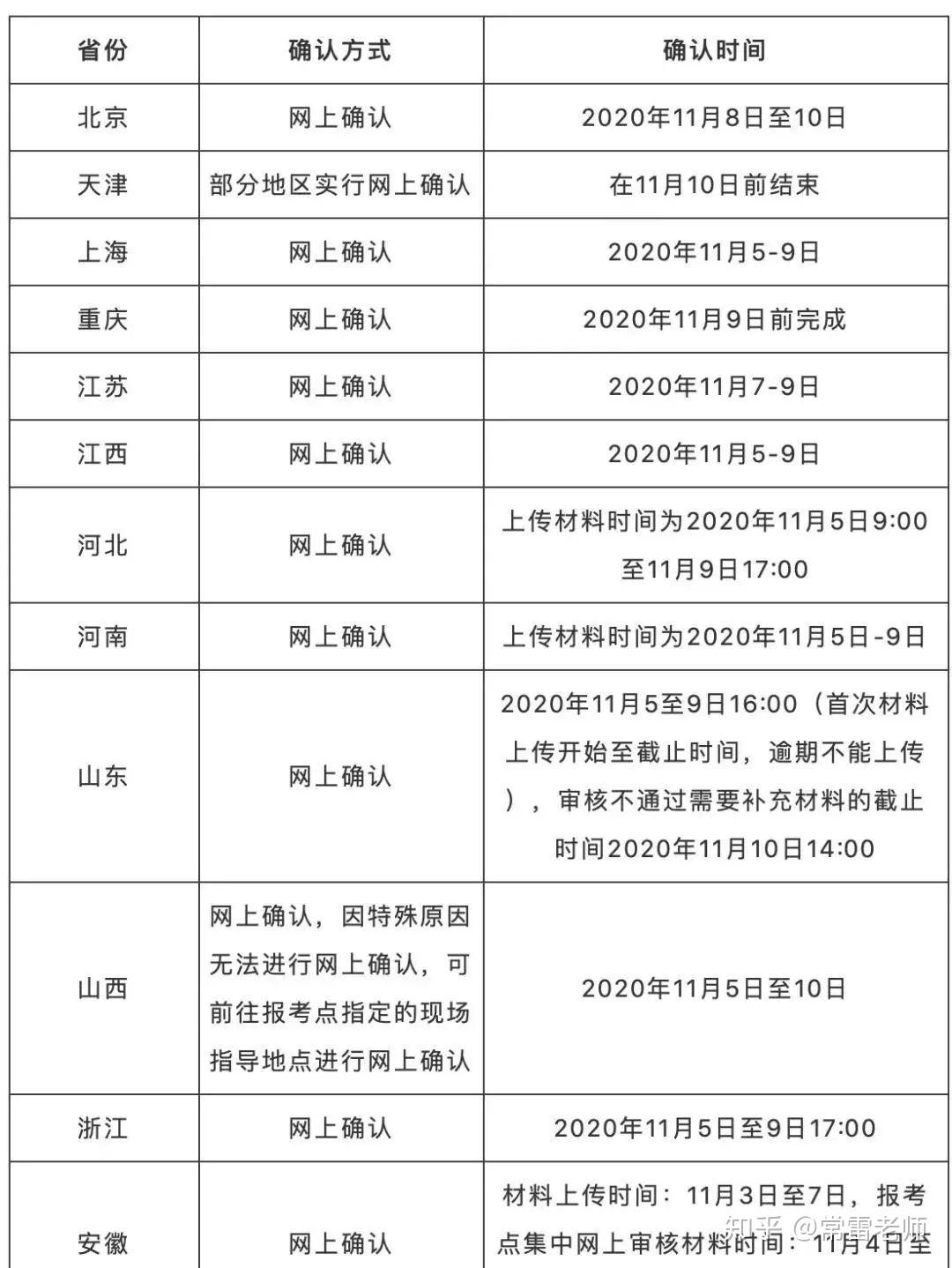
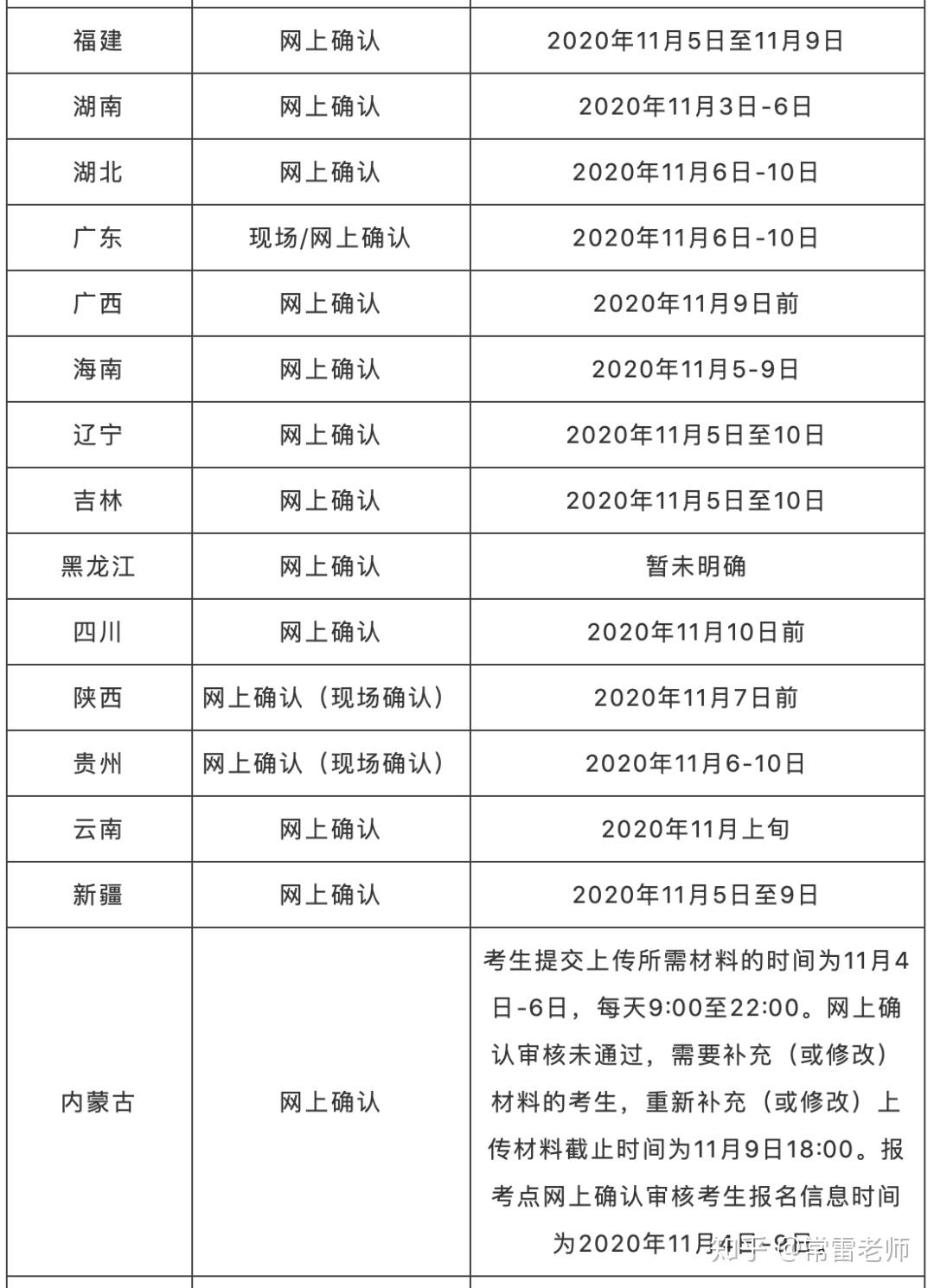

虽然说大多数考点的现场确认时间和省级网报公告一致,但是也有好几种例外情况,
1、省级现场确认时间只是一个整体的范围
省级现场确认时间只是一个整体的范围,有部分考点会在省级网报公告的规定的实际范围内,自行确定一个现场确认时间。
当其他考点可能已经开始现场确认的时候,它还没开始现场确认工作,而其他考点可能还可以现场确认而它现场确认已经结束了。
2、考点时间可能比省级网报公告的现场确认时间早
这种情况一般出现在实行网上现场确认的考点。
这种考点还是比较好的,起码在省网报公告说的现场确认时间里还是可以进行现场确认的。
下面的两种情况才是比较坑的。
3. 省网报公告的现场确认时间尚未开始,考点现场确认工作就已经结束了
有部分考点的现场确认时间在研招网是看不到的,需要到所在大学研招网去看。
4、考点现场确认时间开始和结束都比省级现场确认时间早
比如,北京市网报公告要求的确认时间是11月8日-10日,而北京大学报考点公告要求的确认时间是11月2日10:00-10日16:00,比北京市网报公告要求的确认时间提前了6天。而北方工业大学报考点公告要求的确认时间,是11月6日-9日,与北京市网报公告要求的确认时间相比,不仅提前了2天开始确认,而且提前1天结束确认。
因此,大家一定要密切关注自己的报考点采用哪个系统,按要求来网上确认,不要搞错了。
二、2021年研招考生网上确认图像采集标准1、本人近三个月内正面、免冠、无妆、彩色头像电子证件照(蓝色或白色背景,具体以报考点要求为准,用于准考证照片);
2、仅支持jpg或jpeg格式,建议大小不超过10M,宽高比例3:4;
3、正脸头像,人像水平居中,人脸的水平转动角,倾斜角,俯仰角应在±10度之内。眼睛所在位置距离照片上边沿为图像高度的30%-50%之间。头像左右对称。姿态端正,双眼自然睁开并平视,耳朵对称,嘴巴自然闭合,左右肩膀平衡,头部和肩部要端正且不能过大或过小,需占整张照片的比例为不小于2/3
4、脸部无遮挡,头发不得遮挡脸部、眼睛、眉毛、耳朵或造成阴影,要露出五官;
5、照明光线均匀,脸部、鼻部不能发光,无高光、光斑,无阴影、红眼等;
6、人像对焦准确、层次清晰,不模糊;
7、请不要化妆,不得佩戴眼镜、隐形眼镜、美瞳拍照;
8、图像应真实表达考生本人近期相貌,照片内容要求真实有效,不得做任何修改(如不得使用PS等照片编辑软件处理,不得对人像特征(如伤疤、痣、发型等)进行技术处理,不得用照片翻拍);
9、请务必谨慎上传符合上述全部要求的照片,否则会影响审核。三、其他相关材料网上(现场)确认除了照片外,一般还需要提供以下材料,小伙伴们可以先按照进行准备,具体以各自报考点的网报确认要求,以官方要求为准:
1、考生本人有效身份证
2、电子照片(一般是蓝底或红底)
3、报名号
4、注册章盖齐的学生证(应届生)
5、毕业证、学位证原件(非应届生)多数报考点只要毕业证,但有些报考点两者都要,具体以报考点公告为准。
6、学历学籍认证报告(未通过学历学籍校验的考生)对于自考应届生明年才能拿到毕业证的同学,学历学籍校验不通过,请咨询报考点,或者联系报考院校,咨询确认时需要提供哪些证明材料,一定要提前准备好。
7、户口簿或户籍证明(选择户籍所在地报考点的非应届生)
8、工作证明/社保缴费记录/居住证等(选择非户籍所在地报考点的非应届生)
具体需要哪一种,以报考点公告为准。OK,这就是今天关于“现场确认”的相关内容。
现场确认类似于“占座位”,只有现场确认成功的,才能参加初试,今年大部分省市都是在线上确认,其实比线下确认的风险大,要是线下确认,一般都有工作人员,如果你出错,工作人员一定会指出来,但是现在线上确认,就只能靠自己了。
所以大家一定要仔细研究现场确认的要求资料,不要抱着侥幸心理,觉得某个资料不提交没关系,这样是不OK的!
话不多说,大家继续加油吧!
文章来源于网络 如有侵权请联系删除!!!
本篇是新开坑的 音视频编解码之路 的第一篇,这个系列主要通过书籍、网上的博文/代码等渠道,整理与各编码协议相关的资料和自己的理解,同时手撸下对应格式的“编解码器”,形成对真正编解码器的原理的基础认识,从而后续可以进一步研究真正意义上的编解码器如libx264的逻辑与优化。
之前在查找编解码的学习资料时,看到了韦神的经验之谈,因此就以JPEG的编码来开篇吧。
本篇整体脉络来自于手动生成一张JPEG图片,不过针对文章中的诸多细节做了补充和资料汇总,另外把代码也用C++和OOP的方式修改了下。范例工程位于avcodec_tutorial。
基本系统的 JPEG 压缩编码算法一共分为 10 个步骤:
- 颜色模式转换
- 分块
- 离散余弦变换(DCT)
- 量化
- Zigzag 扫描排序
- DC 系数的差分脉冲调制编码(DPCM)
- DC 系数的中间格式计算
- AC 系数的游程编码(RLE)
- AC 系数的中间格式计算
- 熵编码
接下去我们将逐一介绍上述的各个步骤,并在其中穿插涉及的一些概念与实际代码。
JPEG 采用的是 YCbCr 颜色空间,这里不再赘述为啥选择YUV等等重复较多的内容,之前没有接触过的可以看下一文读懂 YUV 的采样与格式和其他资料来补补课。
颜色模式从RGB转为YUV的过程中可以把采样也一起做了,这里Demo采样按照YUV444也就是全采样不做额外处理的方式简单实现,代码如下:
讯享网uint8_t bound(uint8_t min, int value, uint8_t max) {
<span class="k">if</span><span class="p">(</span><span class="n">value</span> <span class="o"><=</span> <span class="n">min</span><span class="p">)</span> <span class="p">{</span> <span class="k">return</span> <span class="n">min</span><span class="p">;</span> <span class="p">}</span> <span class="k">if</span><span class="p">(</span><span class="n">value</span> <span class="o">>=</span> <span class="n">max</span><span class="p">)</span> <span class="p">{</span> <span class="k">return</span> <span class="n">max</span><span class="p">;</span> <span class="p">}</span> <span class="k">return</span> <span class="n">value</span><span class="p">;</span> }
bool JpegEncoder::rgbToYUV444(const uint8_t r, const uint8_t g, const uint8_t *b,
讯享网 <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">,</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="k">const</span> <span class="n">y</span><span class="p">,</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="k">const</span> <span class="n">u</span><span class="p">,</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="k">const</span> <span class="n">v</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">row</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">row</span> <span class="o"><</span> <span class="n">h</span><span class="p">;</span> <span class="n">row</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">column</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">column</span> <span class="o"><</span> <span class="n">w</span><span class="p">;</span> <span class="n">column</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">index</span> <span class="o">=</span> <span class="n">row</span> <span class="o">*</span> <span class="n">w</span> <span class="o">+</span> <span class="n">column</span><span class="p">;</span> <span class="c1">// rgb -> yuv 公式
// 这里在实现的时候踩了个坑 // 之前直接将cast后的值赋值给了y/u/v数组,y/u/v数组类型是uint8,计算出来比如v是256直接越界数值会被转成其他如0之类的值 // 导致最后颜色效果错误 int yValue = static_cast<int>(round(0.299 r[index] + 0.587 g[index] + 0.114 * b[index]));
<span class="kt">int</span> <span class="n">uValue</span> <span class="o">=</span> <span class="k">static_cast</span><span class="o"><</span><span class="kt">int</span><span class="o">></span><span class="p">(</span><span class="n">round</span><span class="p">(</span><span class="o">-</span><span class="mf">0.169</span> <span class="o">*</span> <span class="n">r</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">-</span> <span class="mf">0.331</span> <span class="o">*</span> <span class="n">g</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">+</span> <span class="mf">0.500</span> <span class="o">*</span> <span class="n">b</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">+</span> <span class="mi">128</span><span class="p">));</span> <span class="kt">int</span> <span class="n">vValue</span> <span class="o">=</span> <span class="k">static_cast</span><span class="o"><</span><span class="kt">int</span><span class="o">></span><span class="p">(</span><span class="n">round</span><span class="p">(</span><span class="mf">0.500</span> <span class="o">*</span> <span class="n">r</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">-</span> <span class="mf">0.419</span> <span class="o">*</span> <span class="n">g</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">-</span> <span class="mf">0.081</span> <span class="o">*</span> <span class="n">b</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">+</span> <span class="mi">128</span><span class="p">));</span> <span class="c1">// 做下边界容错 y[index] = bound(0, yValue, 255);
讯享网 <span class="n">u</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">=</span> <span class="n">bound</span><span class="p">(</span><span class="mi">0</span><span class="p">,</span> <span class="n">uValue</span><span class="p">,</span> <span class="mi">255</span><span class="p">);</span> <span class="n">v</span><span class="p">[</span><span class="n">index</span><span class="p">]</span> <span class="o">=</span> <span class="n">bound</span><span class="p">(</span><span class="mi">0</span><span class="p">,</span> <span class="n">vValue</span><span class="p">,</span> <span class="mi">255</span><span class="p">);</span> <span class="p">}</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span>
}
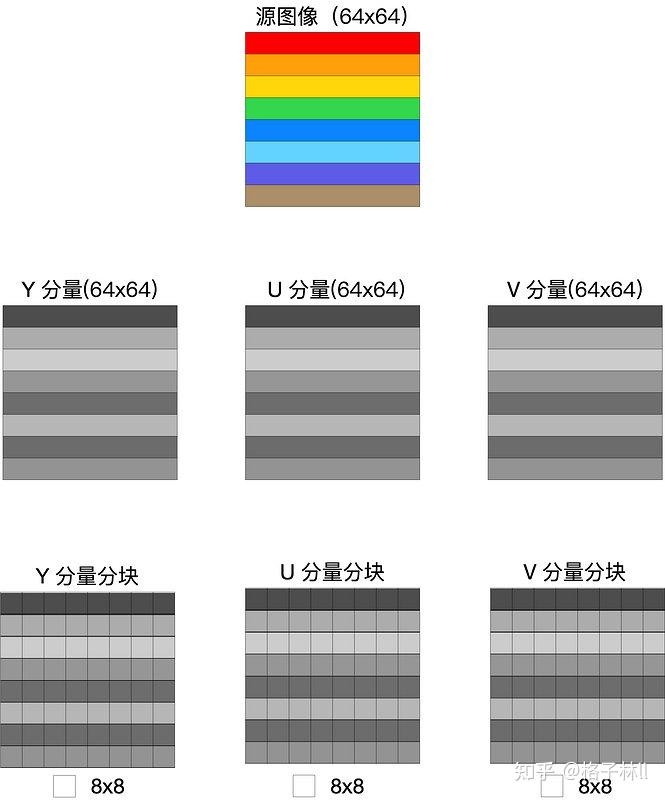
由于后面的 DCT 变换需要对 8x8 的子块进行处理,因此在进行 DCT 变换之前必须把源图像数据进行分块。源图象经过上面的颜色模式转换、采样后变成了 YUV 数据,所以需要分别对 Y U V 三个分量进行分块。具体分块方式为由左及右,由上到下依次读取 8x8 的子块,存放在长度为 64 的数组中,之后再进行 DCT 变换。
因为这个分块机制的原因,有些素材的宽高如果不是8的倍数的话,都需要在处理的时候进行补齐。
bool JpegEncoder::yuvToBlocks(const uint8_t y, const uint8_t u, const uint8_t *v,讯享网 <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">,</span> <span class="kt">uint8_t</span> <span class="n">yBlocks</span><span class="p">[][</span><span class="mi">64</span><span class="p">],</span> <span class="kt">uint8_t</span> <span class="n">uBlocks</span><span class="p">[][</span><span class="mi">64</span><span class="p">],</span> <span class="kt">uint8_t</span> <span class="n">vBlocks</span><span class="p">[][</span><span class="mi">64</span><span class="p">])</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">wBlockSize</span> <span class="o">=</span> <span class="n">w</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">w</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">hBlockSize</span> <span class="o">=</span> <span class="n">h</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">h</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">blockRow</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">blockRow</span> <span class="o"><</span> <span class="n">hBlockSize</span><span class="p">;</span> <span class="n">blockRow</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">blockColumn</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">blockColumn</span> <span class="o"><</span> <span class="n">wBlockSize</span><span class="p">;</span> <span class="n">blockColumn</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">blockIndex</span> <span class="o">=</span> <span class="n">blockRow</span> <span class="o">*</span> <span class="n">wBlockSize</span> <span class="o">+</span> <span class="n">blockColumn</span><span class="p">;</span> <span class="c1">// 当前子块下标
uint8_t *yBlock = yBlocks[blockIndex];
<span class="kt">uint8_t</span> <span class="o">*</span><span class="n">uBlock</span> <span class="o">=</span> <span class="n">uBlocks</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="n">vBlock</span> <span class="o">=</span> <span class="n">vBlocks</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">row</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">row</span> <span class="o"><</span> <span class="mi">8</span><span class="p">;</span> <span class="n">row</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">column</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">column</span> <span class="o"><</span> <span class="mi">8</span><span class="p">;</span> <span class="n">column</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">indexInSubBlock</span> <span class="o">=</span> <span class="n">row</span> <span class="o">*</span> <span class="mi">8</span> <span class="o">+</span> <span class="n">column</span><span class="p">;</span> <span class="c1">// 块中数据位置 int realPosX = blockColumn 8 + column; // 在完整YUV数据中的X位置 int realPosY = blockRow 8 + row; // 在完整YUV数据中的Y位置 int indexInOriginData = realPosY * w + realPosX; // 在原始数据中的位置 if (realPosX >= w || realPosY >= h) {
讯享网 <span class="c1">// 补齐数据
yBlock[indexInSubBlock] = 0;
<span class="n">uBlock</span><span class="p">[</span><span class="n">indexInSubBlock</span><span class="p">]</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">vBlock</span><span class="p">[</span><span class="n">indexInSubBlock</span><span class="p">]</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="p">}</span> <span class="k">else</span> <span class="p">{</span> <span class="n">yBlock</span><span class="p">[</span><span class="n">indexInSubBlock</span><span class="p">]</span> <span class="o">=</span> <span class="n">y</span><span class="p">[</span><span class="n">indexInOriginData</span><span class="p">];</span> <span class="n">uBlock</span><span class="p">[</span><span class="n">indexInSubBlock</span><span class="p">]</span> <span class="o">=</span> <span class="n">u</span><span class="p">[</span><span class="n">indexInOriginData</span><span class="p">];</span> <span class="n">vBlock</span><span class="p">[</span><span class="n">indexInSubBlock</span><span class="p">]</span> <span class="o">=</span> <span class="n">v</span><span class="p">[</span><span class="n">indexInOriginData</span><span class="p">];</span> <span class="p">}</span> <span class="p">}</span> <span class="p">}</span> <span class="p">}</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span> }
分块后的结果类似下面这样,假设源图像像素宽高为64x64,颜色转换并分块后将变成YUV三个通道,且每通道按8x8进行拆分:
JPEG 里要对数据压缩,就需要先要做一次 DCT 变换。数学方面的细节不是目前的重点,只需要知道这个变换是将数据域从时(空)域变换到频域,把图片里点和点间的规律呈现出来,是为了更方便后续的压缩的。
先贴一下公式,对数学原理感兴趣的话可以扩展看看JPEG编码&算术编码、LZW编码等资料:
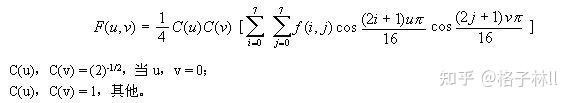
DCT变换与图像压缩、去燥里面还讲到了为什么JPEG选择DCT而不选择DFT的原因。
再贴一下代码:
讯享网/* 外部逻辑 / bool JpegEncoder::blocksFDCT(const uint8_t (yBlocks)[64], const uint8_t (uBlocks)[64], const uint8_t (vBlocks)[64],
<span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">,</span> <span class="kt">int</span> <span class="n">yDCT</span><span class="p">[][</span><span class="mi">64</span><span class="p">],</span> <span class="kt">int</span> <span class="n">uDCT</span><span class="p">[][</span><span class="mi">64</span><span class="p">],</span> <span class="kt">int</span> <span class="n">vDCT</span><span class="p">[][</span><span class="mi">64</span><span class="p">])</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">wBlockSize</span> <span class="o">=</span> <span class="n">w</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">w</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">hBlockSize</span> <span class="o">=</span> <span class="n">h</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">h</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">blockSize</span> <span class="o">=</span> <span class="n">wBlockSize</span> <span class="o">*</span> <span class="n">hBlockSize</span><span class="p">;</span> <span class="n">std</span><span class="o">::</span><span class="n">shared_ptr</span><span class="o"><</span><span class="n">JpegFDCT</span><span class="o">></span> <span class="n">fdct</span> <span class="o">=</span> <span class="n">std</span><span class="o">::</span><span class="n">make_shared</span><span class="o"><</span><span class="n">JpegFDCT</span><span class="o">></span><span class="p">();</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">blockIndex</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">blockIndex</span> <span class="o"><</span> <span class="n">blockSize</span><span class="p">;</span> <span class="n">blockIndex</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="n">yBlock</span> <span class="o">=</span> <span class="n">yBlocks</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="n">uBlock</span> <span class="o">=</span> <span class="n">uBlocks</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="n">vBlock</span> <span class="o">=</span> <span class="n">vBlocks</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">yDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">yBlock</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">-</span> <span class="mi">128</span><span class="p">;</span> <span class="n">uDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">uBlock</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">-</span> <span class="mi">128</span><span class="p">;</span> <span class="n">vDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">vBlock</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">-</span> <span class="mi">128</span><span class="p">;</span> <span class="n">yDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">yDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o"><<</span> <span class="mi">2</span><span class="p">;</span> <span class="n">uDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">uDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o"><<</span> <span class="mi">2</span><span class="p">;</span> <span class="n">vDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">vDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">][</span><span class="n">i</span><span class="p">]</span> <span class="o"><<</span> <span class="mi">2</span><span class="p">;</span> <span class="p">}</span> <span class="n">fdct</span><span class="o">-></span><span class="n">fdct2d8x8</span><span class="p">(</span><span class="n">yDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">]);</span> <span class="n">fdct</span><span class="o">-></span><span class="n">fdct2d8x8</span><span class="p">(</span><span class="n">uDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">]);</span> <span class="n">fdct</span><span class="o">-></span><span class="n">fdct2d8x8</span><span class="p">(</span><span class="n">vDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">]);</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span> }
/* DCT 逻辑 */ JpegFDCT::JpegFDCT() {
讯享网<span class="kt">int</span> <span class="n">i</span><span class="p">,</span> <span class="n">j</span><span class="p">;</span> <span class="kt">float</span> <span class="n">factor</span><span class="p">[</span><span class="mi">64</span><span class="p">];</span> <span class="c1">// 初始化fdct factor
const float AAN_DCT_FACTOR[DCT_SIZE] = {
<span class="mf">1.0f</span><span class="p">,</span> <span class="mf">1.f</span><span class="p">,</span> <span class="mf">1.f</span><span class="p">,</span> <span class="mf">1.f</span><span class="p">,</span> <span class="mf">1.0f</span><span class="p">,</span> <span class="mf">0.f</span><span class="p">,</span> <span class="mf">0.f</span><span class="p">,</span> <span class="mf">0.f</span><span class="p">,</span> <span class="p">};</span> <span class="k">for</span> <span class="p">(</span><span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="n">DCT_SIZE</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="n">DCT_SIZE</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">factor</span><span class="p">[</span><span class="n">i</span> <span class="o">*</span> <span class="mi">8</span> <span class="o">+</span> <span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="mf">1.0f</span> <span class="o">/</span> <span class="p">(</span><span class="n">AAN_DCT_FACTOR</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">*</span> <span class="n">AAN_DCT_FACTOR</span><span class="p">[</span><span class="n">j</span><span class="p">]</span> <span class="o">*</span> <span class="mi">8</span><span class="p">);</span> <span class="p">}</span> <span class="p">}</span> <span class="k">for</span> <span class="p">(</span><span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">mFDCTFactor</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">float2Fix</span><span class="p">(</span><span class="n">factor</span><span class="p">[</span><span class="n">i</span><span class="p">]);</span> <span class="p">}</span> } int JpegFDCT::float2Fix(float value) {
讯享网<span class="k">return</span> <span class="k">static_cast</span><span class="o"><</span><span class="kt">int</span><span class="o">></span><span class="p">(</span><span class="n">value</span> <span class="o">*</span> <span class="p">(</span><span class="mi">1</span> <span class="o"><<</span> <span class="n">FIX_Q</span><span class="p">));</span>
} void JpegFDCT::fdct2d8x8(int data8x8, int ftab) {
<span class="kt">int</span> <span class="n">tmp0</span><span class="p">,</span> <span class="n">tmp1</span><span class="p">,</span> <span class="n">tmp2</span><span class="p">,</span> <span class="n">tmp3</span><span class="p">;</span> <span class="kt">int</span> <span class="n">tmp4</span><span class="p">,</span> <span class="n">tmp5</span><span class="p">,</span> <span class="n">tmp6</span><span class="p">,</span> <span class="n">tmp7</span><span class="p">;</span> <span class="kt">int</span> <span class="n">tmp10</span><span class="p">,</span> <span class="n">tmp11</span><span class="p">,</span> <span class="n">tmp12</span><span class="p">,</span> <span class="n">tmp13</span><span class="p">;</span> <span class="kt">int</span> <span class="n">z1</span><span class="p">,</span> <span class="n">z2</span><span class="p">,</span> <span class="n">z3</span><span class="p">,</span> <span class="n">z4</span><span class="p">,</span> <span class="n">z5</span><span class="p">,</span> <span class="n">z11</span><span class="p">,</span> <span class="n">z13</span><span class="p">;</span> <span class="kt">int</span> <span class="o">*</span><span class="n">dataptr</span><span class="p">;</span> <span class="kt">int</span> <span class="n">ctr</span><span class="p">;</span> <span class="cm">/* Pass 1: process rows. */</span> <span class="n">dataptr</span> <span class="o">=</span> <span class="n">data8x8</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="n">ctr</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">ctr</span> <span class="o"><</span> <span class="n">DCT_SIZE</span><span class="p">;</span> <span class="n">ctr</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">tmp0</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">7</span><span class="p">];</span> <span class="n">tmp7</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">7</span><span class="p">];</span> <span class="n">tmp1</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">6</span><span class="p">];</span> <span class="n">tmp6</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">6</span><span class="p">];</span> <span class="n">tmp2</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">2</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">5</span><span class="p">];</span> <span class="n">tmp5</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">2</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">5</span><span class="p">];</span> <span class="n">tmp3</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">3</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">4</span><span class="p">];</span> <span class="n">tmp4</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">3</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">4</span><span class="p">];</span> <span class="cm">/* Even part */</span> <span class="n">tmp10</span> <span class="o">=</span> <span class="n">tmp0</span> <span class="o">+</span> <span class="n">tmp3</span><span class="p">;</span> <span class="cm">/* phase 2 */</span> <span class="n">tmp13</span> <span class="o">=</span> <span class="n">tmp0</span> <span class="o">-</span> <span class="n">tmp3</span><span class="p">;</span> <span class="n">tmp11</span> <span class="o">=</span> <span class="n">tmp1</span> <span class="o">+</span> <span class="n">tmp2</span><span class="p">;</span> <span class="n">tmp12</span> <span class="o">=</span> <span class="n">tmp1</span> <span class="o">-</span> <span class="n">tmp2</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp10</span> <span class="o">+</span> <span class="n">tmp11</span><span class="p">;</span> <span class="cm">/* phase 3 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">4</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp10</span> <span class="o">-</span> <span class="n">tmp11</span><span class="p">;</span> <span class="n">z1</span> <span class="o">=</span> <span class="p">(</span><span class="n">tmp12</span> <span class="o">+</span> <span class="n">tmp13</span><span class="p">)</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c4 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">2</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp13</span> <span class="o">+</span> <span class="n">z1</span><span class="p">;</span> <span class="cm">/* phase 5 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">6</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp13</span> <span class="o">-</span> <span class="n">z1</span><span class="p">;</span> <span class="cm">/* Odd part */</span> <span class="n">tmp10</span> <span class="o">=</span> <span class="n">tmp4</span> <span class="o">+</span> <span class="n">tmp5</span><span class="p">;</span> <span class="cm">/* phase 2 */</span> <span class="n">tmp11</span> <span class="o">=</span> <span class="n">tmp5</span> <span class="o">+</span> <span class="n">tmp6</span><span class="p">;</span> <span class="n">tmp12</span> <span class="o">=</span> <span class="n">tmp6</span> <span class="o">+</span> <span class="n">tmp7</span><span class="p">;</span> <span class="cm">/* The rotator is modified from fig 4-8 to avoid extra negations. */</span> <span class="n">z5</span> <span class="o">=</span> <span class="p">(</span><span class="n">tmp10</span> <span class="o">-</span> <span class="n">tmp12</span><span class="p">)</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c6 */</span> <span class="n">z2</span> <span class="o">=</span> <span class="p">(</span><span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">*</span> <span class="n">tmp10</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">)</span> <span class="o">+</span> <span class="n">z5</span><span class="p">;</span> <span class="cm">/* c2-c6 */</span> <span class="n">z4</span> <span class="o">=</span> <span class="p">(</span><span class="n">float2Fix</span><span class="p">(</span><span class="mf">1.f</span><span class="p">)</span> <span class="o">*</span> <span class="n">tmp12</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">)</span> <span class="o">+</span> <span class="n">z5</span><span class="p">;</span> <span class="cm">/* c2+c6 */</span> <span class="n">z3</span> <span class="o">=</span> <span class="n">tmp11</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c4 */</span> <span class="n">z11</span> <span class="o">=</span> <span class="n">tmp7</span> <span class="o">+</span> <span class="n">z3</span><span class="p">;</span> <span class="cm">/* phase 5 */</span> <span class="n">z13</span> <span class="o">=</span> <span class="n">tmp7</span> <span class="o">-</span> <span class="n">z3</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">5</span><span class="p">]</span> <span class="o">=</span> <span class="n">z13</span> <span class="o">+</span> <span class="n">z2</span><span class="p">;</span> <span class="cm">/* phase 6 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">3</span><span class="p">]</span> <span class="o">=</span> <span class="n">z13</span> <span class="o">-</span> <span class="n">z2</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">=</span> <span class="n">z11</span> <span class="o">+</span> <span class="n">z4</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="mi">7</span><span class="p">]</span> <span class="o">=</span> <span class="n">z11</span> <span class="o">-</span> <span class="n">z4</span><span class="p">;</span> <span class="n">dataptr</span> <span class="o">+=</span> <span class="n">DCT_SIZE</span><span class="p">;</span> <span class="cm">/* advance pointer to next row */</span> <span class="p">}</span> <span class="cm">/* Pass 2: process columns. */</span> <span class="n">dataptr</span> <span class="o">=</span> <span class="n">data8x8</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="n">ctr</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">ctr</span> <span class="o"><</span> <span class="n">DCT_SIZE</span><span class="p">;</span> <span class="n">ctr</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">tmp0</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">0</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">7</span><span class="p">];</span> <span class="n">tmp7</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">0</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">7</span><span class="p">];</span> <span class="n">tmp1</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">1</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">6</span><span class="p">];</span> <span class="n">tmp6</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">1</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">6</span><span class="p">];</span> <span class="n">tmp2</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">2</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">5</span><span class="p">];</span> <span class="n">tmp5</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">2</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">5</span><span class="p">];</span> <span class="n">tmp3</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">3</span><span class="p">]</span> <span class="o">+</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">4</span><span class="p">];</span> <span class="n">tmp4</span> <span class="o">=</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">3</span><span class="p">]</span> <span class="o">-</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">4</span><span class="p">];</span> <span class="cm">/* Even part */</span> <span class="n">tmp10</span> <span class="o">=</span> <span class="n">tmp0</span> <span class="o">+</span> <span class="n">tmp3</span><span class="p">;</span> <span class="cm">/* phase 2 */</span> <span class="n">tmp13</span> <span class="o">=</span> <span class="n">tmp0</span> <span class="o">-</span> <span class="n">tmp3</span><span class="p">;</span> <span class="n">tmp11</span> <span class="o">=</span> <span class="n">tmp1</span> <span class="o">+</span> <span class="n">tmp2</span><span class="p">;</span> <span class="n">tmp12</span> <span class="o">=</span> <span class="n">tmp1</span> <span class="o">-</span> <span class="n">tmp2</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">0</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp10</span> <span class="o">+</span> <span class="n">tmp11</span><span class="p">;</span> <span class="cm">/* phase 3 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">4</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp10</span> <span class="o">-</span> <span class="n">tmp11</span><span class="p">;</span> <span class="n">z1</span> <span class="o">=</span> <span class="p">(</span><span class="n">tmp12</span> <span class="o">+</span> <span class="n">tmp13</span><span class="p">)</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c4 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">2</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp13</span> <span class="o">+</span> <span class="n">z1</span><span class="p">;</span> <span class="cm">/* phase 5 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">6</span><span class="p">]</span> <span class="o">=</span> <span class="n">tmp13</span> <span class="o">-</span> <span class="n">z1</span><span class="p">;</span> <span class="cm">/* Odd part */</span> <span class="n">tmp10</span> <span class="o">=</span> <span class="n">tmp4</span> <span class="o">+</span> <span class="n">tmp5</span><span class="p">;</span> <span class="cm">/* phase 2 */</span> <span class="n">tmp11</span> <span class="o">=</span> <span class="n">tmp5</span> <span class="o">+</span> <span class="n">tmp6</span><span class="p">;</span> <span class="n">tmp12</span> <span class="o">=</span> <span class="n">tmp6</span> <span class="o">+</span> <span class="n">tmp7</span><span class="p">;</span> <span class="cm">/* The rotator is modified from fig 4-8 to avoid extra negations. */</span> <span class="n">z5</span> <span class="o">=</span> <span class="p">(</span><span class="n">tmp10</span> <span class="o">-</span> <span class="n">tmp12</span><span class="p">)</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c6 */</span> <span class="n">z2</span> <span class="o">=</span> <span class="p">(</span><span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">*</span> <span class="n">tmp10</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">)</span> <span class="o">+</span> <span class="n">z5</span><span class="p">;</span> <span class="cm">/* c2-c6 */</span> <span class="n">z4</span> <span class="o">=</span> <span class="p">(</span><span class="n">float2Fix</span><span class="p">(</span><span class="mf">1.f</span><span class="p">)</span> <span class="o">*</span> <span class="n">tmp12</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">)</span> <span class="o">+</span> <span class="n">z5</span><span class="p">;</span> <span class="cm">/* c2+c6 */</span> <span class="n">z3</span> <span class="o">=</span> <span class="n">tmp11</span> <span class="o">*</span> <span class="n">float2Fix</span><span class="p">(</span><span class="mf">0.f</span><span class="p">)</span> <span class="o">>></span> <span class="n">FIX_Q</span><span class="p">;</span> <span class="cm">/* c4 */</span> <span class="n">z11</span> <span class="o">=</span> <span class="n">tmp7</span> <span class="o">+</span> <span class="n">z3</span><span class="p">;</span> <span class="cm">/* phase 5 */</span> <span class="n">z13</span> <span class="o">=</span> <span class="n">tmp7</span> <span class="o">-</span> <span class="n">z3</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">5</span><span class="p">]</span> <span class="o">=</span> <span class="n">z13</span> <span class="o">+</span> <span class="n">z2</span><span class="p">;</span> <span class="cm">/* phase 6 */</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">3</span><span class="p">]</span> <span class="o">=</span> <span class="n">z13</span> <span class="o">-</span> <span class="n">z2</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">1</span><span class="p">]</span> <span class="o">=</span> <span class="n">z11</span> <span class="o">+</span> <span class="n">z4</span><span class="p">;</span> <span class="n">dataptr</span><span class="p">[</span><span class="n">DCT_SIZE</span> <span class="o">*</span> <span class="mi">7</span><span class="p">]</span> <span class="o">=</span> <span class="n">z11</span> <span class="o">-</span> <span class="n">z4</span><span class="p">;</span> <span class="n">dataptr</span><span class="o">++</span><span class="p">;</span> <span class="cm">/* advance pointer to next column */</span> <span class="p">}</span> <span class="n">ftab</span> <span class="o">=</span> <span class="n">ftab</span> <span class="o">?</span> <span class="nl">ftab</span> <span class="p">:</span> <span class="n">mFDCTFactor</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="n">ctr</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">ctr</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">ctr</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">ctr</span><span class="p">]</span> <span class="o">*=</span> <span class="n">ftab</span><span class="p">[</span><span class="n">ctr</span><span class="p">];</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">ctr</span><span class="p">]</span> <span class="o">>>=</span> <span class="n">FIX_Q</span> <span class="o">+</span> <span class="mi">2</span><span class="p">;</span> <span class="p">}</span> }
JPEG 里是对每 8x8 个点作为一个单位处理的,上述代码就是对我们刚才所划分好的各个 8x8 的子块进行DCT变换。首先我们看到在进行变换前需要将矩阵中的每个数值减去 128,然后再一一带入 DCT 变换公式,这是因为 DCT 公式所接受的数字范围是 -128 到 127 之间,其目的在于使像素的绝对值出现3位10进制的概率大大减少。其他部分的处理逻辑暂时没有去深究。
假定有一个8x8的图像数据如下图所示:
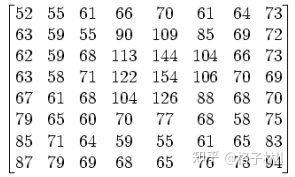
那么在减去128之后,将变成:

再经过DCT变换,最终将变成DCT系数矩阵:

对应于u=0,v=0的系数,称做直流分量,即DC系数,即位于矩阵的最左上角,上图是-415的位置 对于除DC系数意外的矩阵中的其余 63 个则称为是交流系数(AC)
DCT 输出的频率系数矩阵中最左上角的直流(DC)系数幅度最大,以 DC 系数为出发点向下、向右的其它 DCT 系数,离 DC 分量越远,频率越高,幅度值越小,即图像信息的大部分集中于直流系数及其附近的低频频谱上,离 DC 系数越来越远的高频频谱几乎不含图像信息,甚至于只含杂波。这个点从数据上的理解可以看下JPEG压缩原理与DCT离散余弦变换中量化与反量化部分。
关于图像频率可以扩展看下图像上的频率指的是什么。
量化是对经过 FDCT(解码为IDCT) 变换后的频率系数进行量化,是一个将信号的幅度离散化的过程,量化过程实际上就是对 DCT 系数的一个优化过程,它是利用了人眼对高频部分不敏感的特性来实现数据的大幅简化。在这个过程实际上是简单地把频率领域上每个成份,除以一个对于该成份的常数,且接着四舍五入取最接近的整数,这就是整个过程中的主要有损运算。
从结果来看,这个过程经常会把很多高频率的成份四舍五入而接近0,且剩下很多会变成小的正或负数。而整个量化的目的正是减小非“0”系数的幅度以及增加“0”值系数的数目,量化是图像质量下降的最主要原因,量化表也是控制 JPEG 压缩比的关键。
因为人眼对亮度信号比对色差信号更敏感,因此使用了两种量化表:亮度量化值和色差量化值。
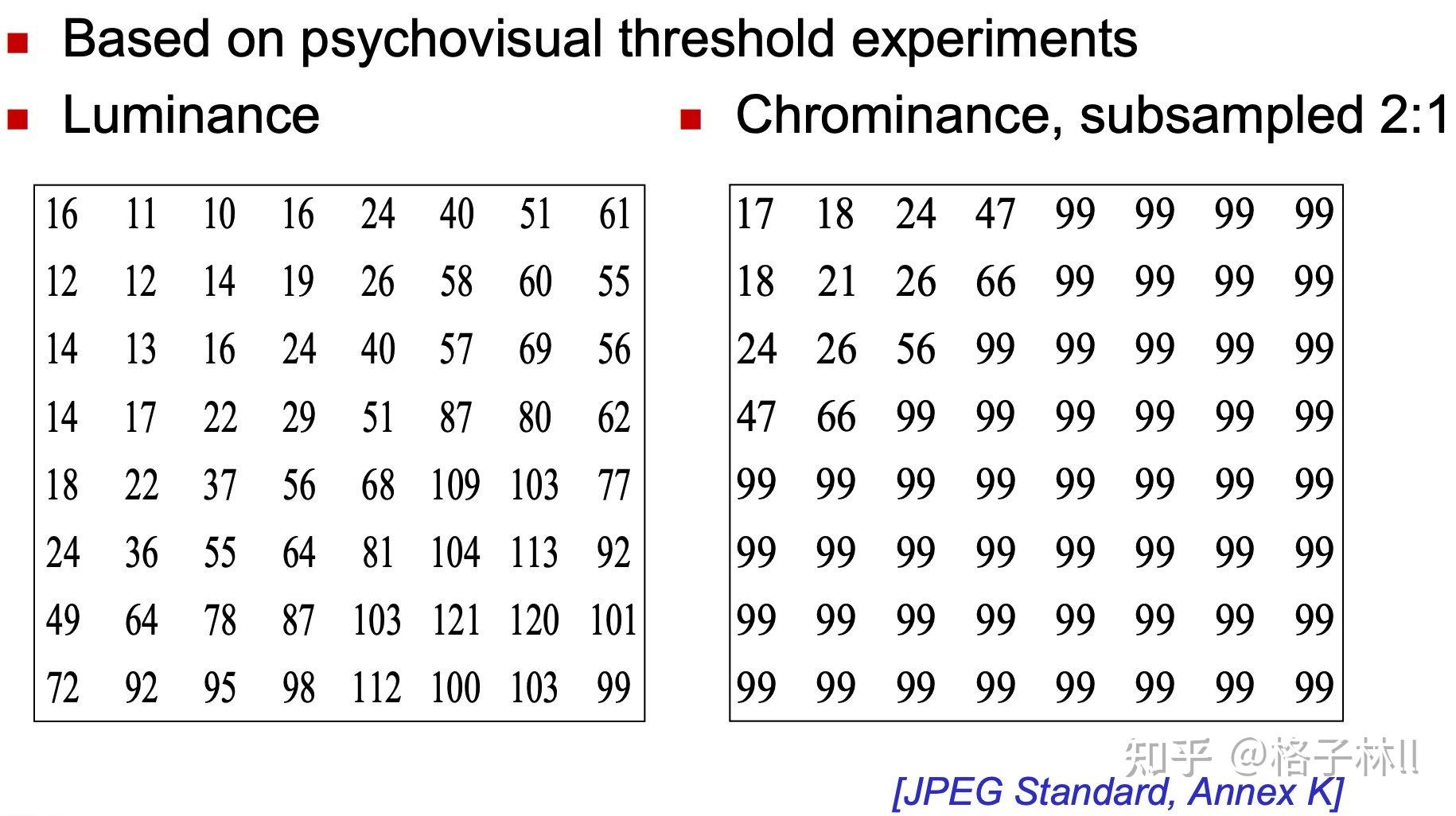
将前面所得到的 DCT 系数矩阵与上图中的亮度/色度量化矩阵进行相除并四舍五入后可得到:

总体来说这个过程就类似于是一个空间域的低通滤波器,对 Y 分量采用细量化,对 UV 采用粗量化,对低频细量化,对高频粗量化。对于滤波器感兴趣的话可以扩展看看这篇文章:常见低通、高通、带通三种滤波器的工作原理
JPEG压缩比例,就是通过控制量化的多少来控制。比如,上面的量化矩阵,如果我们把矩阵的每个数都double一下,那是不是会出现更多的0了?说不定都只有DC系数非0,其他都是0,如果是这样那编码时就可以更省空间了,N个0只要一个游程编码搞定,数据量超小。但也意味着,恢复时,会带来更多的误差,图像质量也会变差了。
虽然量化步骤除掉了一些高频量,也就是损失了高频细节,但事实上人眼对高空间频率远没有低频敏感,所以处理后的视觉损失很小。另一个重要原因是所有图片的点与点之间会有一个色彩过渡的过程,大量的图像信息被包含在低频率中,经过量化处理后,在高频率段,将出现大量连续的零。对于这部分可以扩展阅读下为什么说图像的低频是轮廓,高频是噪声和细节以及图像压缩中,为什么要将图像从空间域转换到频率域
讯享网/* 外部逻辑 */ bool JpegEncoder::fdctToQuant(int yDCT[][64], int uDCT[][64], int vDCT[][64],
<span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">wBlockSize</span> <span class="o">=</span> <span class="n">w</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">w</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">hBlockSize</span> <span class="o">=</span> <span class="n">h</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">h</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">blockSize</span> <span class="o">=</span> <span class="n">wBlockSize</span> <span class="o">*</span> <span class="n">hBlockSize</span><span class="p">;</span> <span class="n">std</span><span class="o">::</span><span class="n">shared_ptr</span><span class="o"><</span><span class="n">JpegQuant</span><span class="o">></span> <span class="n">quant</span> <span class="o">=</span> <span class="n">std</span><span class="o">::</span><span class="n">make_shared</span><span class="o"><</span><span class="n">JpegQuant</span><span class="o">></span><span class="p">();</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">blockIndex</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">blockIndex</span> <span class="o"><</span> <span class="n">blockSize</span><span class="p">;</span> <span class="n">blockIndex</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="o">*</span><span class="n">yBlock</span> <span class="o">=</span> <span class="n">yDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">int</span> <span class="o">*</span><span class="n">uBlock</span> <span class="o">=</span> <span class="n">uDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">int</span> <span class="o">*</span><span class="n">vBlock</span> <span class="o">=</span> <span class="n">vDCT</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="n">quant</span><span class="o">-></span><span class="n">quantEncode8x8</span><span class="p">(</span><span class="n">yBlock</span><span class="p">,</span> <span class="nb">true</span><span class="p">);</span> <span class="n">quant</span><span class="o">-></span><span class="n">quantEncode8x8</span><span class="p">(</span><span class="n">uBlock</span><span class="p">,</span> <span class="nb">false</span><span class="p">);</span> <span class="n">quant</span><span class="o">-></span><span class="n">quantEncode8x8</span><span class="p">(</span><span class="n">vBlock</span><span class="p">,</span> <span class="nb">false</span><span class="p">);</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span> }
/* 量化逻辑 / void JpegQuant::quantEncode8x8(int data8x8, bool luminance) {
讯享网<span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">if</span> <span class="p">(</span><span class="n">luminance</span><span class="p">)</span> <span class="p">{</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">/=</span> <span class="n">STD_QUANT_TAB_LUMIN</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="p">}</span> <span class="k">else</span> <span class="p">{</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">/=</span> <span class="n">STD_QUANT_TAB_CHROM</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="p">}</span> <span class="p">}</span>
}
量化后的数据,有一个很大的特点,就是直流分量相对于交流分量来说要大,而且交流分量中含有大量的 0。这样,对这个量化后的数据如何来进行简化,从而再更大程度地进行压缩呢?
这就出现了“Z”字形编排的想法,主要思路就是从左上角第一个像素开始以Z字形进行编排:
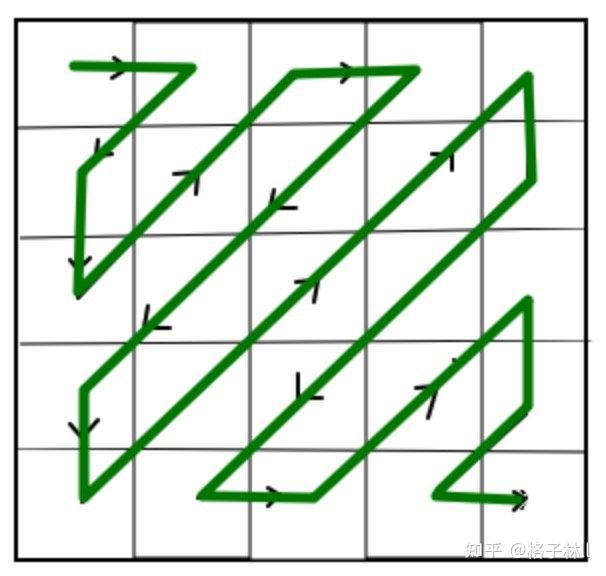
至于为什么使用 Zigzag 进行扫描排序,我个人认为主要是因为图像信息的大部分集中于直流系数及其附近的低频频谱上,离 DC 系数越来越远的高频频谱几乎不含图像信息,因此通过该方式可以将更多的高频数据排序到一起,以便于后续的游程编码(RLE:Run Length Coding)对它们进行编码。大家可以对照上面量化后的矩阵看下使用ZigZag排序与不使用的话0数据的连续性上的差异。
/* 外部逻辑 */ bool JpegEncoder::quantToZigzag(int yQuant[][64], int uQuant[][64], int vQuant[][64],讯享网 <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">wBlockSize</span> <span class="o">=</span> <span class="n">w</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">w</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">hBlockSize</span> <span class="o">=</span> <span class="n">h</span> <span class="o">/</span> <span class="mi">8</span> <span class="o">+</span> <span class="p">(</span><span class="n">h</span> <span class="o">%</span> <span class="mi">8</span> <span class="o">==</span> <span class="mi">0</span> <span class="o">?</span> <span class="mi">0</span> <span class="o">:</span> <span class="mi">1</span><span class="p">);</span> <span class="kt">int</span> <span class="n">blockSize</span> <span class="o">=</span> <span class="n">wBlockSize</span> <span class="o">*</span> <span class="n">hBlockSize</span><span class="p">;</span> <span class="n">std</span><span class="o">::</span><span class="n">shared_ptr</span><span class="o"><</span><span class="n">JpegZigzag</span><span class="o">></span> <span class="n">zigzag</span> <span class="o">=</span> <span class="n">std</span><span class="o">::</span><span class="n">make_shared</span><span class="o"><</span><span class="n">JpegZigzag</span><span class="o">></span><span class="p">();</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">blockIndex</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">blockIndex</span> <span class="o"><</span> <span class="n">blockSize</span><span class="p">;</span> <span class="n">blockIndex</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="o">*</span><span class="n">yBlock</span> <span class="o">=</span> <span class="n">yQuant</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">int</span> <span class="o">*</span><span class="n">uBlock</span> <span class="o">=</span> <span class="n">uQuant</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="kt">int</span> <span class="o">*</span><span class="n">vBlock</span> <span class="o">=</span> <span class="n">vQuant</span><span class="p">[</span><span class="n">blockIndex</span><span class="p">];</span> <span class="n">zigzag</span><span class="o">-></span><span class="n">zigzag</span><span class="p">(</span><span class="n">yBlock</span><span class="p">);</span> <span class="n">zigzag</span><span class="o">-></span><span class="n">zigzag</span><span class="p">(</span><span class="n">uBlock</span><span class="p">);</span> <span class="n">zigzag</span><span class="o">-></span><span class="n">zigzag</span><span class="p">(</span><span class="n">vBlock</span><span class="p">);</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span>
}
/* 排序逻辑 / void JpegZigzag::zigzag(int const data8x8) {
<span class="kt">int</span> <span class="n">temp</span><span class="p">[</span><span class="mi">64</span><span class="p">];</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">temp</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">ZIGZAG_INDEX</span><span class="p">[</span><span class="n">i</span><span class="p">]];</span> <span class="p">}</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">data8x8</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="o">=</span> <span class="n">temp</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="p">}</span> }
8x8 图像块经过 DCT 变换之后得到的 DC 直流系数有两个特点,一是系数的数值比较大,二是相邻 8x8 图像块的 DC 系数值变化不大。根据这个特点,JPEG 算法使用了差分脉冲调制编码 (DPCM) 技术,对相邻图像块之间量化DC系数的差值 (Delta) 进行编码。
讯享网DC(0)=0 Delta = DC(i) - DC(i-1)
此部分代码混杂在最后熵编码的整个流程中,截取部分代码:
… // DC 系数的差分脉冲调制编码(DPCM) diff = block[0] - dc; dc = block[0]; code = diff; // 对code做中间格式计算 … JPEG 中为了更进一步节约空间,并不直接保存数据的具体数值,而是将数据按照位数分为 16 组,保存在表里面。这也就是所谓的变长整数编码 VLI。即,第 0 组中保存的编码位数为 0,其编码所代表的数字为 0;第 1 组中保存的编码位数为 1,编码所代表的数字为 -1 或者 1 ……,如下面的表格所示,这里,暂且称其为 VLI 编码表:

如果 DC 系数差值为 3,通过查找 VLI 可以发现,整数 3 位于 VLI 表格的第 2 组,因此,可以写成(2)(3)的形式,这里的2代表后面的数字(3)的编码长度为2位,该形式称之为 DC 系数的中间格式。
对于VLI可以扩展阅读下可变长度整数的编码,这类思想核心就是用较小的空间存储小数字,而用较大的空间存储大数字,采用这种算法来对整数进行编码是有意义的,它可以节省存储数据需要的空间或者传输数据时所需的带宽。
讯享网// 接上一章节最后传入其Code可进行DC系数的中间格式计算 // 这里category的命名如果觉得不好理解可以进一步去看下 // https://sce.umkc.edu/faculty-sites/lizhu/teaching/2018.fall.video-com/notes/lec04.pdf 第16页 void HuffmanCodec::categoryEncode(int &code, int &size) {
<span class="kt">unsigned</span> <span class="n">absc</span> <span class="o">=</span> <span class="n">abs</span><span class="p">(</span><span class="n">code</span><span class="p">);</span> <span class="kt">unsigned</span> <span class="n">mask</span> <span class="o">=</span> <span class="p">(</span><span class="mi">1</span> <span class="o"><<</span> <span class="mi">15</span><span class="p">);</span> <span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">15</span><span class="p">;</span> <span class="k">if</span> <span class="p">(</span><span class="n">absc</span> <span class="o">==</span> <span class="mi">0</span><span class="p">)</span> <span class="p">{</span> <span class="n">size</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="k">return</span><span class="p">;</span> <span class="p">}</span> <span class="k">while</span> <span class="p">(</span><span class="n">i</span> <span class="o">&&</span> <span class="o">!</span><span class="p">(</span><span class="n">absc</span> <span class="o">&</span> <span class="n">mask</span><span class="p">))</span> <span class="p">{</span> <span class="n">mask</span> <span class="o">>>=</span> <span class="mi">1</span><span class="p">;</span> <span class="n">i</span><span class="o">--</span><span class="p">;</span> <span class="p">}</span> <span class="n">size</span> <span class="o">=</span> <span class="n">i</span> <span class="o">+</span> <span class="mi">1</span><span class="p">;</span> <span class="k">if</span> <span class="p">(</span><span class="n">code</span> <span class="o"><</span> <span class="mi">0</span><span class="p">)</span> <span class="p">{</span> <span class="n">code</span> <span class="o">=</span> <span class="p">(</span><span class="mi">1</span> <span class="o"><<</span> <span class="n">size</span><span class="p">)</span> <span class="o">-</span> <span class="n">absc</span> <span class="o">-</span> <span class="mi">1</span><span class="p">;</span> <span class="p">}</span> }
游程编码 RLC(Run Length Coding)是一种比较简单的压缩算法,其基本思想是将重复且连续出现多次的字符使用(连续出现次数,字符)来描述,从而来更进一步降低数据的传输量,举例来说,一组数据“AAAABBBCCDEEEE”,由4个A、3个B、2个C、1个D、4个E组成,经过RLC可将数据压缩为4A3B2C1D4E(由14个单位转成10个单位)。简而言之,其优点在于将重复性高的数据量压缩成小单位,然而,其缺点在于─若该数据出现频率不高,可能导致压缩结果数据量比原始数据量大,例如:原始数据“ABCDE”,压缩结果为“1A1B1C1D1E”(由5个单位转成10个单位)。
但是,在JPEG编码中,RLC的含义就同其原有的意义略有不同。在JPEG编码中,假设RLC编码之后得到了一个(M,N)的数据对,其中M是两个非零AC系数之间连续的0的个数(即,行程长度),N是下一个非零的AC系数的值。采用这样的方式进行表示,是因为AC系数当中有大量的0,而采用Zigzag扫描也会使得AC系数中有很多连续的0的存在,如此一来,便非常适合于用RLC进行编码。
举个例子来解释一下,假设有以下数据:
57, 45, 0, 0, 0, 0, 23, 0, -30, -8, 0, 0, 1, 000…
经过 0 RLC 之后:
(0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)
注意,如果 AC 系数之间连续 0 的个数超过 16,则需要用一个扩展字节 (15,0) 来表示 16 连续的 0。这是因为后面 huffman 编码的要求,每组数字前一个表示 0 的数量的必须是 4 bit,因此只能是 0~15,所以,如果有这么一组数字:
57, 十八个0, 3, 0, 0, 0, 0, 2, 三十三个0, 895, EOB
我们实际这样编码:
(0,57) ; (15,0) (2,3) ; (4,2) ; (15,0) (15,0) (1,895) , (0,0) 注意 (15,0) 表示了 16 个连续的 0。
EOB:EOB 是一个结束标记, 表示后面都是 0 了。我们用 (0,0) 表示 EOB,但是,如果这组数字不以 0 结束, 那么就不需要 EOB。
讯享网/* RLE的数据 */ typedef struct {
unsigned runlen : 4; unsigned codesize : 4; unsigned codedata : 16; } RLEITEM;
// AC 系数的游程长度编码(RLE)
讯享网// AC 系数的中间格式计算 // rle encode for ac
for (i = 1, j = 0, n = 0, eob = 0; i < 64 && j < 63; i++) {

if (du[i] == 0 && n < 15) { n++; } else { code = du[i]; size = 0; // AC 系数的中间格式计算 categoryEncode(code, size); rlelist[j].runlen = n; rlelist[j].codesize = size; rlelist[j].codedata = code; n = 0; j++; if (size != 0) { eob = j; } } } // 设置 eob if (du[63] == 0) {
讯享网rlelist[eob].runlen = 0; rlelist[eob].codesize = 0; rlelist[eob].codedata = 0; j = eob + 1;
}
以DC 系数的中间格式计算中的编码表以及AC 系数的 RLE中所举例的RLC后的数据为例:
(0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)
我们只处理每对数据中右边的那个数,对其进行 VLI 编码 :查找上面的 VLI 编码表,可以发现,57 在第 6 组当中,因此可以将其写成 (0,6),57 的形式,该形式便称之为 AC 系数的中间格式。
同样的 (0,45) 的中间格式为 (0,6),45 ;(1,-30) 的中间格式为 (1,5),-30 。
该部分在上面章节中已有涉及,就不贴代码了。
在得到 DC 系数的中间格式和 AC 系数的中间格式之后,为进一步压缩图像数据,有必要对两者进行熵编码,通过对出现概率较高的字符采用较小的 bit 数编码达到压缩的目的。JPEG 标准具体规定了两种熵编码方式:Huffman 编码和算术编码。JPEG 基本系统规定采用 Huffman 编码。
熵编码的介绍可以扩展阅读下三分钟学习 | 熵编码,简单说熵编码就是在信息熵的极限范围内进行编码,即无损压缩。
Huffman 编码:对出现概率大的字符分配字符长度较短的二进制编码,对出现概率小的字符分配字符长度较长的二进制编码,从而使得字符的平均编码长度最短。Huffman 编码的原理可以扩展阅读下算法科普:有趣的霍夫曼编码。
Huffman 编码时 DC 系数与 AC 系数分别采用不同的 Huffman 编码表,对于亮度和色度也采用不同的 Huffman 编码表。因此,需要 4 张 Huffman 编码表才能完成熵编码的工作,等到具体 Huffman 编码时再采用查表的方式来高效地完成。然而,在 JPEG 标准中没有定义缺省的 Huffman 表,用户可以根据实际应用自由选择,也可以使用 JPEG 标准推荐的 Huffman 表,或者预先定义一个通用的 Huffman 表,也可以针对一副特定的图像,在压缩编码前通过搜集其统计特征来计算 Huffman 表的值。
结合 Huffman 编码以及上述的DPCM、RLE以及对应的中间格式,参照VLI编码表,我们再来整体地通过一个例子解释下数据最终压缩后的样子:
假定经过RLE之后有如下AC数据:
(0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)
只处理每对数右边的那个:
| 57 是第 6 组的, 实际保存值为 , 所以被编码为 (6,)
| 45 , 同样的操作, 编码为 (6,)
| 23 -> (5,10111)
| -30 -> (5,00001)
| -8 -> (4,0111)
| 1 -> (1,1)
最后,最开始的那串数字就变成了:
(0,6), ; (0,6), ; (4,5), 10111; (1,5), 00001; (0,4) , 0111 ; (2,1), 1 ; (0,0)
括号里的数值正好合成一个字节,后面被编码的数字表示范围是 -32767..32767。合成的字节里,高 4 位是前续 0 的个数,低 4 位描述了后面数字的位数。
再进一步通过 Huffman 查找得到如果 (0,6) 的 huffman 编码为 ,那么最终编码的数据便是:
最后看下DC的编码,假设DC的diff值是-511,编码为 (9, 000000000) ,如果 9 的 Huffman 编码是 ,那么在 JPG 文件中, DC 的 2 进制表示为000000000,最终加上上面AC的第一个数据,编码为:
000000000 …
/* 初始化编码表 */ HuffmanCodec::HuffmanCodec() {讯享网<span class="n">initCoddList</span><span class="p">(</span><span class="nb">true</span><span class="p">,</span> <span class="nb">true</span><span class="p">);</span> <span class="n">initCoddList</span><span class="p">(</span><span class="nb">true</span><span class="p">,</span> <span class="nb">false</span><span class="p">);</span> <span class="n">initCoddList</span><span class="p">(</span><span class="nb">false</span><span class="p">,</span> <span class="nb">true</span><span class="p">);</span> <span class="n">initCoddList</span><span class="p">(</span><span class="nb">false</span><span class="p">,</span> <span class="nb">false</span><span class="p">);</span>
void HuffmanCodec::initCoddList(bool dc, bool luminance) {
<span class="kt">int</span> <span class="n">i</span><span class="p">,</span> <span class="n">j</span><span class="p">,</span> <span class="n">k</span><span class="p">;</span> <span class="kt">int</span> <span class="n">symbol</span><span class="p">;</span> <span class="kt">int</span> <span class="n">code</span><span class="p">;</span> <span class="kt">uint8_t</span> <span class="n">hufsize</span><span class="p">[</span><span class="mi">256</span><span class="p">];</span> <span class="kt">int</span> <span class="n">hufcode</span><span class="p">[</span><span class="mi">256</span><span class="p">];</span> <span class="kt">int</span> <span class="n">tabsize</span><span class="p">;</span> <span class="n">k</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">code</span> <span class="o">=</span> <span class="mh">0x00</span><span class="p">;</span> <span class="k">const</span> <span class="kt">uint8_t</span> <span class="o">*</span><span class="n">hufTable</span><span class="p">;</span> <span class="n">HUFCODEITEM</span> <span class="o">*</span><span class="n">codeList</span><span class="p">;</span> <span class="k">if</span> <span class="p">(</span><span class="n">dc</span> <span class="o">&&</span> <span class="n">luminance</span><span class="p">)</span> <span class="p">{</span> <span class="n">hufTable</span> <span class="o">=</span> <span class="n">STD_HUFTAB_LUMIN_DC</span><span class="p">;</span> <span class="n">codeList</span> <span class="o">=</span> <span class="n">mCodeListDCLumin</span><span class="p">;</span> <span class="p">}</span> <span class="k">else</span> <span class="nf">if</span> <span class="p">(</span><span class="n">dc</span> <span class="o">&&</span> <span class="o">!</span><span class="n">luminance</span><span class="p">)</span> <span class="p">{</span> <span class="n">hufTable</span> <span class="o">=</span> <span class="n">STD_HUFTAB_CHROM_DC</span><span class="p">;</span> <span class="n">codeList</span> <span class="o">=</span> <span class="n">mCodeListDCChrom</span><span class="p">;</span> <span class="p">}</span> <span class="k">else</span> <span class="nf">if</span> <span class="p">(</span><span class="o">!</span><span class="n">dc</span> <span class="o">&&</span> <span class="n">luminance</span><span class="p">)</span> <span class="p">{</span> <span class="n">hufTable</span> <span class="o">=</span> <span class="n">STD_HUFTAB_LUMIN_AC</span><span class="p">;</span> <span class="n">codeList</span> <span class="o">=</span> <span class="n">mCodeListACLumin</span><span class="p">;</span> <span class="p">}</span> <span class="k">else</span> <span class="p">{</span> <span class="n">hufTable</span> <span class="o">=</span> <span class="n">STD_HUFTAB_CHROM_AC</span><span class="p">;</span> <span class="n">codeList</span> <span class="o">=</span> <span class="n">mCodeListACChrom</span><span class="p">;</span> <span class="p">}</span> <span class="k">for</span> <span class="p">(</span><span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="n">MAX_HUFFMAN_CODE_LEN</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="n">hufTable</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">hufsize</span><span class="p">[</span><span class="n">k</span><span class="p">]</span> <span class="o">=</span> <span class="n">i</span> <span class="o">+</span> <span class="mi">1</span><span class="p">;</span> <span class="n">hufcode</span><span class="p">[</span><span class="n">k</span><span class="p">]</span> <span class="o">=</span> <span class="n">code</span><span class="p">;</span> <span class="n">code</span><span class="o">++</span><span class="p">;</span> <span class="n">k</span><span class="o">++</span><span class="p">;</span> <span class="p">}</span> <span class="n">code</span> <span class="o"><<=</span> <span class="mi">1</span><span class="p">;</span> <span class="p">}</span> <span class="n">tabsize</span> <span class="o">=</span> <span class="n">k</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="n">tabsize</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">symbol</span> <span class="o">=</span> <span class="n">hufTable</span><span class="p">[</span><span class="n">MAX_HUFFMAN_CODE_LEN</span> <span class="o">+</span> <span class="n">i</span><span class="p">];</span> <span class="n">codeList</span><span class="p">[</span><span class="n">symbol</span><span class="p">].</span><span class="n">depth</span> <span class="o">=</span> <span class="n">hufsize</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="n">codeList</span><span class="p">[</span><span class="n">symbol</span><span class="p">].</span><span class="n">code</span> <span class="o">=</span> <span class="n">hufcode</span><span class="p">[</span><span class="n">i</span><span class="p">];</span> <span class="p">}</span> } /* 编码 / bool HuffmanCodec::huffmanEncode(HUFCODEITEM codeList, int size) {
讯享网<span class="kt">unsigned</span> <span class="n">code</span><span class="p">;</span> <span class="kt">int</span> <span class="n">len</span><span class="p">;</span> <span class="k">if</span> <span class="p">(</span><span class="o">!</span><span class="n">mBitStream</span><span class="p">)</span> <span class="p">{</span> <span class="k">return</span> <span class="nb">false</span><span class="p">;</span> <span class="p">}</span> <span class="n">code</span> <span class="o">=</span> <span class="n">codeList</span><span class="p">[</span><span class="n">size</span><span class="p">].</span><span class="n">code</span><span class="p">;</span> <span class="n">len</span> <span class="o">=</span> <span class="n">codeList</span><span class="p">[</span><span class="n">size</span><span class="p">].</span><span class="n">depth</span><span class="p">;</span> <span class="k">if</span> <span class="p">(</span><span class="n">EOF</span> <span class="o">==</span> <span class="n">bitstr_put_bits</span><span class="p">(</span><span class="n">mBitStream</span><span class="p">,</span> <span class="n">code</span><span class="p">,</span> <span class="n">len</span><span class="p">))</span> <span class="p">{</span> <span class="k">return</span> <span class="nb">false</span><span class="p">;</span> <span class="p">}</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span>
}
JPEG 文件大体上可以分成两个部分:标记码(Tag)和压缩数据。
常用的标记有 SOI、APP0、APPn、DQT、SOF0、DHT、DRI、SOS、EOI:
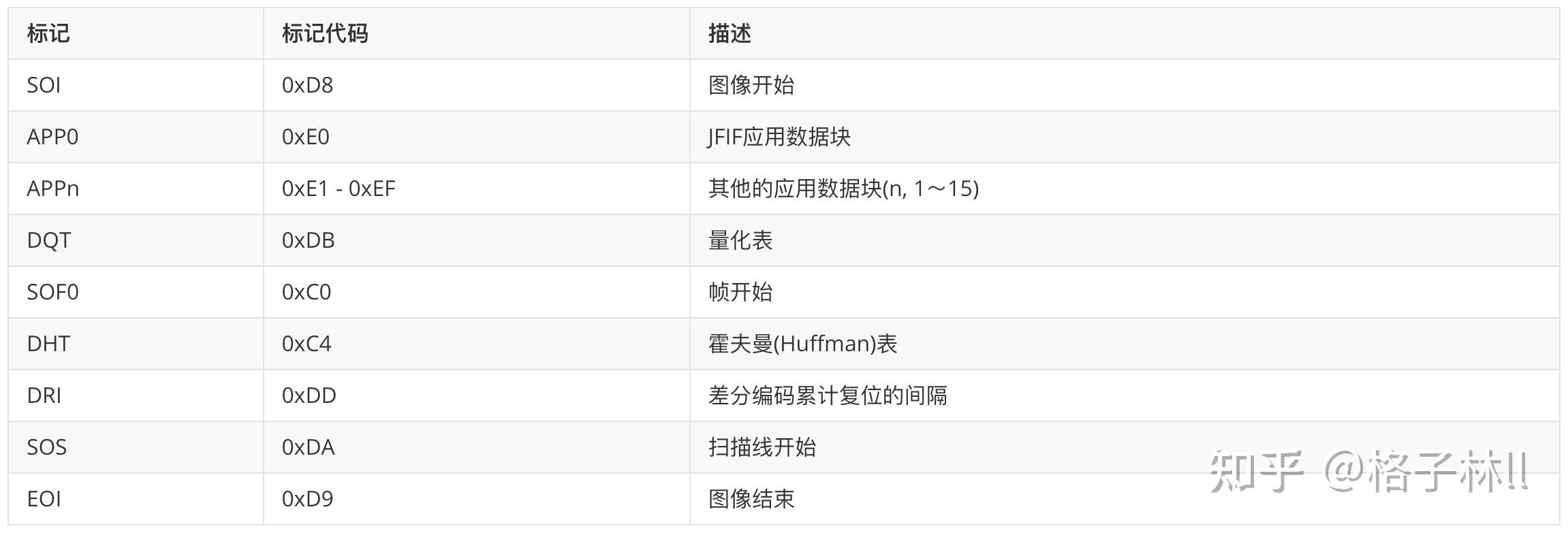
更具体的细节可扩展阅读下JPEG文件格式详解。
bool JpegEncoder::writeToFile(char* buffer, long dataLength,讯享网 <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">w</span><span class="p">,</span> <span class="k">const</span> <span class="kt">unsigned</span> <span class="kt">int</span> <span class="o">&</span><span class="n">h</span><span class="p">)</span> <span class="p">{</span> <span class="n">FILE</span> <span class="o">*</span><span class="n">fp</span> <span class="o">=</span> <span class="n">fopen</span><span class="p">(</span><span class="n">mOutputPath</span><span class="p">.</span><span class="n">data</span><span class="p">(),</span> <span class="s">"wb"</span><span class="p">);</span> <span class="c1">// SOI
fputc(0xff, fp);
<span class="n">fputc</span><span class="p">(</span><span class="mh">0xd8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="c1">// DQT const int *pqtab[2] = {JpegQuant::STD_QUANT_TAB_LUMIN, JpegQuant::STD_QUANT_TAB_CHROM};
讯享网<span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">2</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="kt">int</span> <span class="n">len</span> <span class="o">=</span> <span class="mi">2</span> <span class="o">+</span> <span class="mi">1</span> <span class="o">+</span> <span class="mi">64</span><span class="p">;</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xff</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xdb</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">i</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="mi">64</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">fputc</span><span class="p">(</span><span class="n">pqtab</span><span class="p">[</span><span class="n">i</span><span class="p">][</span><span class="n">JpegZigzag</span><span class="o">::</span><span class="n">ZIGZAG_INDEX</span><span class="p">[</span><span class="n">j</span><span class="p">]],</span> <span class="n">fp</span><span class="p">);</span> <span class="p">}</span> <span class="p">}</span> <span class="c1">// SOF0
int SOF0Len = 2 + 1 + 2 + 2 + 1 + 3 * 3;
<span class="n">fputc</span><span class="p">(</span><span class="mh">0xff</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xc0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">SOF0Len</span> <span class="o">>></span> <span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">SOF0Len</span> <span class="o">>></span> <span class="mi">0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="c1">// precision 8bit fputc(h >> 8, fp); // height fputc(h >> 0, fp); // height fputc(w >> 8, fp); // width fputc(w >> 0, fp); // width fputc(3, fp);
讯享网<span class="n">fputc</span><span class="p">(</span><span class="mh">0x01</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x11</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x00</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x02</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x11</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x01</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x03</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x11</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x01</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="c1">// DHT AC
const uint8_t *huftabAC[] = {
<span class="n">HuffmanCodec</span><span class="o">::</span><span class="n">STD_HUFTAB_LUMIN_AC</span><span class="p">,</span> <span class="n">HuffmanCodec</span><span class="o">::</span><span class="n">STD_HUFTAB_CHROM_AC</span> <span class="p">};</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">2</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xff</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xc4</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="kt">int</span> <span class="n">len</span> <span class="o">=</span> <span class="mi">2</span> <span class="o">+</span> <span class="mi">1</span> <span class="o">+</span> <span class="mi">16</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="mi">16</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">len</span> <span class="o">+=</span> <span class="n">huftabAC</span><span class="p">[</span><span class="n">i</span><span class="p">][</span><span class="n">j</span><span class="p">];</span> <span class="p">}</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">i</span> <span class="o">+</span> <span class="mh">0x10</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fwrite</span><span class="p">(</span><span class="n">huftabAC</span><span class="p">[</span><span class="n">i</span><span class="p">],</span> <span class="n">len</span> <span class="o">-</span> <span class="mi">3</span><span class="p">,</span> <span class="mi">1</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="p">}</span> <span class="c1">// DHT DC const uint8_t *huftabDC[] = {
讯享网 <span class="n">HuffmanCodec</span><span class="o">::</span><span class="n">STD_HUFTAB_LUMIN_DC</span><span class="p">,</span> <span class="n">HuffmanCodec</span><span class="o">::</span><span class="n">STD_HUFTAB_CHROM_DC</span> <span class="p">};</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">i</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">i</span> <span class="o"><</span> <span class="mi">2</span><span class="p">;</span> <span class="n">i</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xff</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xc4</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="kt">int</span> <span class="n">len</span> <span class="o">=</span> <span class="mi">2</span> <span class="o">+</span> <span class="mi">1</span> <span class="o">+</span> <span class="mi">16</span><span class="p">;</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="mi">16</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">len</span> <span class="o">+=</span> <span class="n">huftabDC</span><span class="p">[</span><span class="n">i</span><span class="p">][</span><span class="n">j</span><span class="p">];</span> <span class="p">}</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">len</span> <span class="o">>></span> <span class="mi">0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">i</span> <span class="o">+</span> <span class="mh">0x00</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fwrite</span><span class="p">(</span><span class="n">huftabDC</span><span class="p">[</span><span class="n">i</span><span class="p">],</span> <span class="n">len</span> <span class="o">-</span> <span class="mi">3</span><span class="p">,</span> <span class="mi">1</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="p">}</span> <span class="c1">// SOS
int SOSLen = 2 + 1 + 2 * 3 + 3;
<span class="n">fputc</span><span class="p">(</span><span class="mh">0xff</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0xda</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">SOSLen</span> <span class="o">>></span> <span class="mi">8</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="n">SOSLen</span> <span class="o">>></span> <span class="mi">0</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mi">3</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x01</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x00</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x02</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x11</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x03</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x11</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x00</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x3F</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fputc</span><span class="p">(</span><span class="mh">0x00</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="c1">// data fwrite(buffer, dataLength, 1, fp);
讯享网<span class="c1">// EOI
fputc(0xff, fp);
<span class="n">fputc</span><span class="p">(</span><span class="mh">0xd9</span><span class="p">,</span> <span class="n">fp</span><span class="p">);</span> <span class="n">fflush</span><span class="p">(</span><span class="n">fp</span><span class="p">);</span> <span class="n">fclose</span><span class="p">(</span><span class="n">fp</span><span class="p">);</span> <span class="k">return</span> <span class="nb">true</span><span class="p">;</span> }
到这里我们编写的JpegEncoder就可以将传入的RGB24格式的数据压缩编码成YUV444的JPEG文件了,可以运行 avcodec_tutorial 项目,运行后将在你的桌面看到如下内容随机生成的图片:

手动生成一张JPEG图片
JPEG 简易文档
JPEG图像压缩算法流程详解
JPEG编解码原理及代码调试
JPEG standard
Variable Length Coding (VLC) in JPEG
JPEG编码&算术编码、LZW编码
图像的时频变换——离散余弦变换
图像上的频率指的是什么
为什么说图像的低频是轮廓,高频是噪声和细节
DCT变换与图像压缩、去燥
JPEG压缩原理与DCT离散余弦变换
JPEG 标准推荐的亮度、色度DC、AC Huffman 编码表
一文读懂 YUV 的采样与格式
JPEG文件格式详解
数据压缩之游程编码
要出门了,在我出片率极高的富士GS645s里装上了细腻的黑白胶片伊尔富Delta 100 120

顺手拿起富士XT3 XF 35mm f2给它留个影。再一看外边多云,天气开始回暖,一派午后光线漫反射带来的低动态曝光景色,

带上一台富士GW690?装上富士velvia 100 120 反转片吗?
悉尼还在lockdown,冲洗反转片要等到周一邮寄。干嘛不干脆直接带着GS645s和富士XT3出门呢?

我们有的时候因为形式而忘记了内容。

fuji velvia simulation
NR-4, H-1 S+2 Sharp+2

Classic Chrome

Kodachrome simulation
NR-4, H+1,S+2,Sharp+2,WB red+2 Blue+5,DR 200

AcrosII simulation
NR-4, H-1 S+2 Sharp+2

Acros Red filter simulation
NR-4, H+2,S+2,Sharp+4,Red filter

Acros Yellow Filter simulation
NR-4, H+1, S+2,Sharp+3,yellow filter

Acros Red Filter simulation
NR-4, H+2,S+2,Sharp+4,DR200,Red filter
在大部分ISP系统中,一般都是先从RAW到RGB然后再转到YUV进行压缩编码存储,出于编写仿真系统的原因,需要实现一个UYVY也就是YUV422格式的压缩编码,网上找了一圈基本都是说libjpeg是事实标准,以libjpeg关键字基本都是RGB数据压缩编解码的例子,关于YUV数据的操作范例寥寥。查阅了libjpeg的readme.txt以后成功地把UYVY压缩编码成jpeg,本文纯应用记录分享,不涉及YUV转DCT系数,以及霍夫曼编码等细节;
好了,let‘s roll。
几个细节问题:
- libjpeg默认以8x8像素为一个block进行压缩编码,所以图像最好是8的偶数倍长宽,如果不是,则需要事先进行补齐,补齐内容默认是最后一行,一列的重复;
- UYVY排列需要转换为planar排列,就是说Y占一个连续空间,然后是U连续空间,再然后是V连续空间;
- 正确的设置压缩数据的色域,YUV downsample ratio;
- 使用jpeg_write_raw_data()代替jpeg_write_scanlines(),根据UV downsample ratio设置每次写入的行数,对于YUV422来说,UV只是image width减半,高度不变,因此每次写入8行即可,如果是YUV420,则每次需要写入16行Y,8行UV数据;
讯享网#include <stdio.h> #include “jpeglib.h” #include <setjmp.h> #include <stdlib.h> #include <string.h> #include <stdint.h> int main() {
<span class="k">struct</span> <span class="n">jpeg_compress_struct</span> <span class="n">cinfo</span><span class="p">;</span> <span class="k">struct</span> <span class="n">jpeg_error_mgr</span> <span class="n">jerr</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">err</span> <span class="o">=</span> <span class="n">jpeg_std_error</span><span class="p">(</span><span class="o">&</span><span class="n">jerr</span><span class="p">);</span> <span class="n">jpeg_create_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="n">FILE</span><span class="o">*</span> <span class="n">infile</span> <span class="o">=</span> <span class="nb">NULL</span><span class="p">;</span> <span class="n">fopen_s</span><span class="p">(</span><span class="o">&</span><span class="n">infile</span><span class="p">,</span> <span class="s">"https://www.zhihu.com/topic//_ATM8636_yuv422conv_dump.yuv"</span><span class="p">,</span> <span class="s">"rb"</span><span class="p">);</span> <span class="c1">//UYVY if (infile == NULL)
讯享网<span class="p">{</span> <span class="n">jpeg_destroy_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="k">return</span> <span class="n">EXIT_FAILURE</span><span class="p">;</span> <span class="p">}</span> <span class="k">const</span> <span class="n">int32_t</span> <span class="n">width</span> <span class="o">=</span> <span class="mi">6016</span><span class="p">;</span> <span class="k">const</span> <span class="n">int32_t</span> <span class="n">height</span> <span class="o">=</span> <span class="mi">4016</span><span class="p">;</span> <span class="n">uint8_t</span><span class="o">*</span> <span class="n">buffer</span> <span class="o">=</span> <span class="p">(</span><span class="n">uint8_t</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">uint8_t</span><span class="p">)</span><span class="o">*</span><span class="n">width</span><span class="o">*</span><span class="n">height</span> <span class="o">*</span> <span class="mi">2</span><span class="p">);</span> <span class="n">fread</span><span class="p">(</span><span class="n">buffer</span><span class="p">,</span> <span class="k">sizeof</span><span class="p">(</span><span class="n">uint8_t</span><span class="p">),</span> <span class="n">width</span><span class="o">*</span><span class="n">height</span> <span class="o">*</span> <span class="mi">2</span><span class="p">,</span> <span class="n">infile</span><span class="p">);</span> <span class="n">fclose</span><span class="p">(</span><span class="n">infile</span><span class="p">);</span> <span class="n">uint8_t</span><span class="o">*</span> <span class="n">buffer_y</span> <span class="o">=</span> <span class="p">(</span><span class="n">uint8_t</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">uint8_t</span><span class="p">)</span><span class="o">*</span><span class="n">width</span><span class="o">*</span><span class="n">height</span><span class="p">);</span> <span class="n">uint8_t</span><span class="o">*</span> <span class="n">buffer_u</span> <span class="o">=</span> <span class="p">(</span><span class="n">uint8_t</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">uint8_t</span><span class="p">)</span><span class="o">*</span><span class="n">width</span><span class="o">*</span><span class="n">height</span><span class="o">/</span><span class="mi">2</span><span class="p">);</span> <span class="n">uint8_t</span><span class="o">*</span> <span class="n">buffer_v</span> <span class="o">=</span> <span class="p">(</span><span class="n">uint8_t</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">uint8_t</span><span class="p">)</span><span class="o">*</span><span class="n">width</span><span class="o">*</span><span class="n">height</span><span class="o">/</span><span class="mi">2</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="n">int32_t</span> <span class="n">row</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">row</span> <span class="o"><</span> <span class="n">height</span><span class="p">;</span> <span class="n">row</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">for</span> <span class="p">(</span><span class="n">int32_t</span> <span class="n">col</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">col</span> <span class="o"><</span> <span class="n">width</span> <span class="o">*</span> <span class="mi">2</span><span class="p">;</span> <span class="n">col</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="k">if</span> <span class="p">(</span><span class="n">col</span> <span class="o">%</span> <span class="mi">2</span> <span class="o">==</span> <span class="mi">1</span><span class="p">)</span> <span class="p">{</span> <span class="n">buffer_y</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">+</span> <span class="p">(</span><span class="n">col</span><span class="o">-</span><span class="mi">1</span><span class="p">)</span><span class="o">/</span><span class="mi">2</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">*</span> <span class="mi">2</span> <span class="o">+</span> <span class="n">col</span><span class="p">];</span> <span class="p">}</span> <span class="k">else</span> <span class="k">if</span> <span class="p">(</span><span class="n">col</span> <span class="o">%</span> <span class="mi">4</span> <span class="o">==</span> <span class="mi">0</span><span class="p">)</span> <span class="c1">//U
{
<span class="n">buffer_u</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">/</span> <span class="mi">2</span> <span class="o">+</span> <span class="n">col</span> <span class="o">/</span> <span class="mi">4</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">*</span> <span class="mi">2</span> <span class="o">+</span> <span class="n">col</span><span class="p">];</span> <span class="p">}</span> <span class="k">else</span> <span class="k">if</span> <span class="p">(</span><span class="n">col</span> <span class="o">%</span> <span class="mi">4</span> <span class="o">==</span> <span class="mi">2</span><span class="p">)</span> <span class="c1">//V {
讯享网 <span class="n">buffer_v</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">/</span> <span class="mi">2</span> <span class="o">+</span> <span class="n">col</span> <span class="o">/</span> <span class="mi">4</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer</span><span class="p">[</span><span class="n">row</span><span class="o">*</span><span class="n">width</span> <span class="o">*</span> <span class="mi">2</span> <span class="o">+</span> <span class="n">col</span><span class="p">];</span> <span class="p">}</span> <span class="p">}</span> <span class="p">}</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer</span><span class="p">);</span> <span class="n">FILE</span><span class="o">*</span> <span class="n">outfile</span> <span class="o">=</span> <span class="nb">NULL</span><span class="p">;</span> <span class="n">fopen_s</span><span class="p">(</span><span class="o">&</span><span class="n">outfile</span><span class="p">,</span> <span class="s">"https://www.zhihu.com/topic//yuv422-out-4016-6016.jpg"</span><span class="p">,</span> <span class="s">"wb"</span><span class="p">);</span> <span class="k">if</span> <span class="p">(</span><span class="n">outfile</span> <span class="o">==</span> <span class="nb">NULL</span><span class="p">)</span> <span class="p">{</span> <span class="n">jpeg_destroy_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_y</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_u</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_v</span><span class="p">);</span> <span class="k">return</span> <span class="n">EXIT_FAILURE</span><span class="p">;</span> <span class="p">}</span> <span class="n">jpeg_stdio_dest</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">,</span> <span class="n">outfile</span><span class="p">);</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">image_width</span> <span class="o">=</span> <span class="n">width</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">image_height</span> <span class="o">=</span> <span class="n">height</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">input_components</span> <span class="o">=</span> <span class="mi">3</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">in_color_space</span> <span class="o">=</span> <span class="n">JCS_YCbCr</span><span class="p">;</span> <span class="n">jpeg_set_defaults</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">raw_data_in</span> <span class="o">=</span> <span class="n">TRUE</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">do_fancy_downsampling</span> <span class="o">=</span> <span class="n">FALSE</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">h_samp_factor</span> <span class="o">=</span> <span class="mi">2</span><span class="p">;</span> <span class="c1">//for Y
cinfo.comp_info[0].v_samp_factor = 1;
<span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">h_samp_factor</span> <span class="o">=</span> <span class="mi">1</span><span class="p">;</span> <span class="c1">//for Cb cinfo.comp_info[1].v_samp_factor = 1;
讯享网<span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">h_samp_factor</span> <span class="o">=</span> <span class="mi">1</span><span class="p">;</span> <span class="c1">//for Cr
cinfo.comp_info[2].v_samp_factor = 1;
<span class="n">printf</span><span class="p">(</span><span class="s">"block size=%d</span><span class="se">\n</span><span class="s">"</span><span class="p">,</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">);</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">width_in_blocks</span> <span class="o">=</span> <span class="n">width</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">height_in_blocks</span> <span class="o">=</span> <span class="n">height</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">width_in_blocks</span> <span class="o">=</span> <span class="p">(</span><span class="n">width</span><span class="o">/</span><span class="mi">2</span><span class="p">)</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">height_in_blocks</span> <span class="o">=</span> <span class="n">height</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">width_in_blocks</span> <span class="o">=</span> <span class="p">(</span><span class="n">width</span><span class="o">/</span><span class="mi">2</span><span class="p">)</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">height_in_blocks</span> <span class="o">=</span> <span class="n">height</span> <span class="o">/</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">JSAMPARRAY</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">3</span><span class="p">];</span> <span class="n">JSAMPARRAY</span> <span class="n">y_ptr</span><span class="p">;</span> <span class="n">JSAMPARRAY</span> <span class="n">u_ptr</span><span class="p">;</span> <span class="n">JSAMPARRAY</span> <span class="n">v_ptr</span><span class="p">;</span> <span class="kt">int</span> <span class="n">y_row_stride</span><span class="p">,</span> <span class="n">y_col_stride</span><span class="p">;</span> <span class="c1">//unsigned int y_row_blocks, y_col_blocks; int u_row_stride, u_col_stride, v_row_stride, v_col_stride;
讯享网<span class="n">y_row_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">width_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">y_col_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">height_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">u_row_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">width_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">u_col_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">height_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">v_row_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">width_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">v_col_stride</span> <span class="o">=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">height_in_blocks</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">printf</span><span class="p">(</span><span class="s">"y width=%d, height=%d, u width=%d, height=%d, v width=%d, height=%d</span><span class="se">\n</span><span class="s">"</span><span class="p">,</span> <span class="n">y_row_stride</span><span class="p">,</span> <span class="n">y_col_stride</span><span class="p">,</span> <span class="n">u_row_stride</span><span class="p">,</span> <span class="n">u_col_stride</span><span class="p">,</span> \ <span class="n">v_row_stride</span><span class="p">,</span> <span class="n">v_col_stride</span><span class="p">);</span> <span class="n">y_ptr</span> <span class="o">=</span> <span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="o">*</span><span class="n">y_col_stride</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="n">y_col_stride</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">y_ptr</span><span class="p">[</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer_y</span> <span class="o">+</span> <span class="n">y_row_stride</span> <span class="o">*</span> <span class="n">j</span><span class="p">;</span> <span class="p">}</span> <span class="n">u_ptr</span> <span class="o">=</span> <span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="o">*</span><span class="n">u_col_stride</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="n">u_col_stride</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">u_ptr</span><span class="p">[</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer_u</span> <span class="o">+</span> <span class="n">u_row_stride</span> <span class="o">*</span> <span class="n">j</span><span class="p">;</span> <span class="p">}</span> <span class="n">v_ptr</span> <span class="o">=</span> <span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="n">malloc</span><span class="p">(</span><span class="k">sizeof</span><span class="p">(</span><span class="n">JSAMPROW</span><span class="o">*</span><span class="p">)</span><span class="o">*</span><span class="n">v_col_stride</span><span class="p">);</span> <span class="k">for</span> <span class="p">(</span><span class="kt">int</span> <span class="n">j</span> <span class="o">=</span> <span class="mi">0</span><span class="p">;</span> <span class="n">j</span> <span class="o"><</span> <span class="n">v_col_stride</span><span class="p">;</span> <span class="n">j</span><span class="o">++</span><span class="p">)</span> <span class="p">{</span> <span class="n">v_ptr</span><span class="p">[</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">buffer_v</span> <span class="o">+</span> <span class="n">v_row_stride</span> <span class="o">*</span> <span class="n">j</span><span class="p">;</span> <span class="p">}</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">=</span> <span class="n">y_ptr</span><span class="p">;</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">=</span> <span class="n">u_ptr</span><span class="p">;</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">2</span><span class="p">]</span> <span class="o">=</span> <span class="n">v_ptr</span><span class="p">;</span> <span class="n">jpeg_start_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">,</span> <span class="n">TRUE</span><span class="p">);</span> <span class="k">while</span> <span class="p">(</span><span class="n">cinfo</span><span class="p">.</span><span class="n">next_scanline</span> <span class="o"><</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">image_height</span><span class="p">)</span> <span class="p">{</span> <span class="n">jpeg_write_raw_data</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">,</span> <span class="n">yuvbuffer</span><span class="p">,</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">v_samp_factor</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">);</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">+=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">0</span><span class="p">].</span><span class="n">v_samp_factor</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">+=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">1</span><span class="p">].</span><span class="n">v_samp_factor</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="n">yuvbuffer</span><span class="p">[</span><span class="mi">2</span><span class="p">]</span> <span class="o">+=</span> <span class="n">cinfo</span><span class="p">.</span><span class="n">comp_info</span><span class="p">[</span><span class="mi">2</span><span class="p">].</span><span class="n">v_samp_factor</span><span class="o">*</span><span class="n">cinfo</span><span class="p">.</span><span class="n">block_size</span><span class="p">;</span> <span class="p">}</span> <span class="n">free</span><span class="p">(</span><span class="n">y_ptr</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">u_ptr</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">v_ptr</span><span class="p">);</span> <span class="n">jpeg_finish_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="n">jpeg_destroy_compress</span><span class="p">(</span><span class="o">&</span><span class="n">cinfo</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_y</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_u</span><span class="p">);</span> <span class="n">free</span><span class="p">(</span><span class="n">buffer_v</span><span class="p">);</span> <span class="k">return</span> <span class="mi">0</span><span class="p">;</span>
}
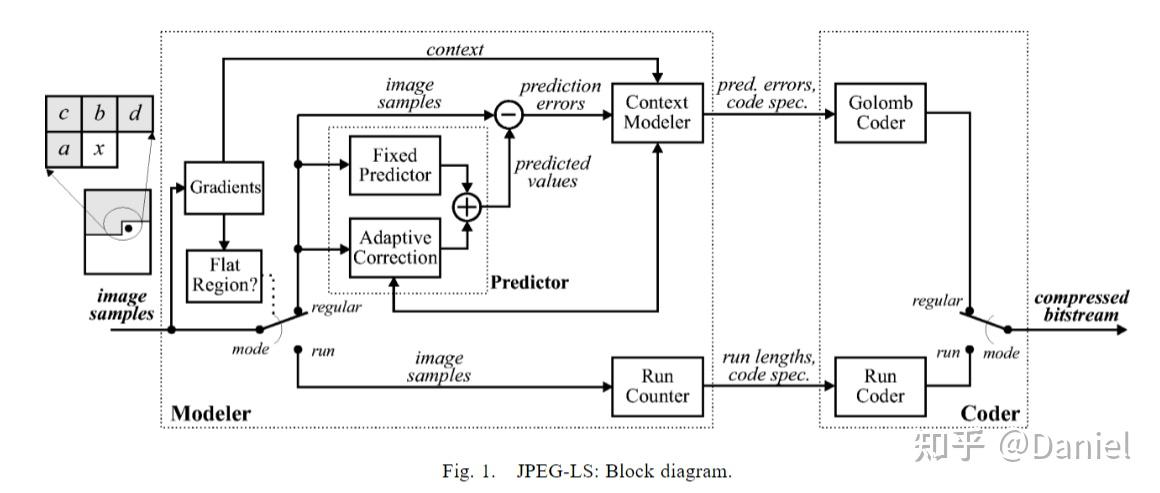
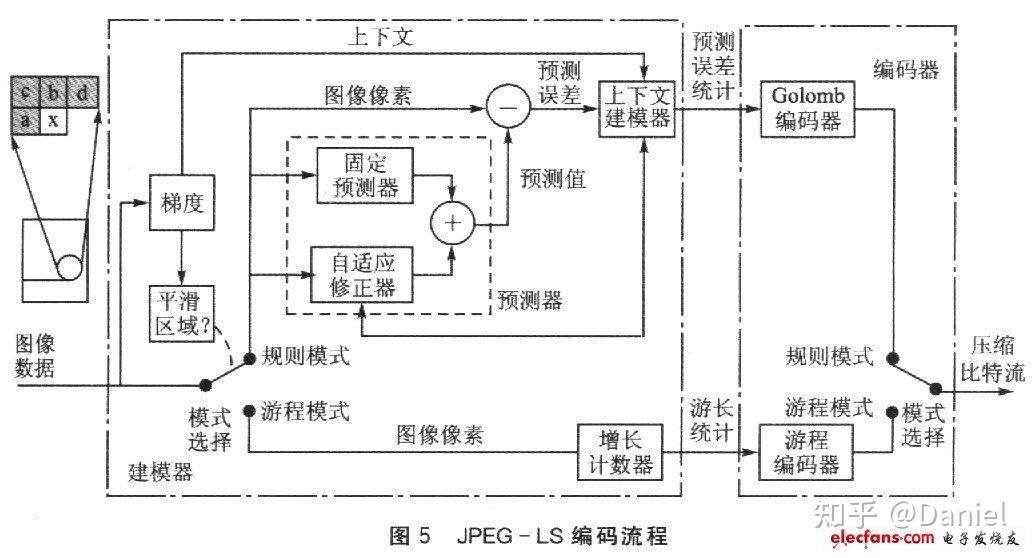
本文是基于论文
The LOCO-I lossless image compression algorithm: principles and standardization into JPEG-LS
写作而成,该论文系统地,详细地介绍了JPEG-LS的工作原理以及理论基础.
JPEG-LS是一种对连续色调图像的无损或者近无损的压缩标准,它的官方名称叫做:ISO-14495-1/ITU-T.87。它是由独立且有区别的建模阶段和编码阶段组成,其简单而又有效。JPEG-LS追求一种更加低复杂度的无损或者近似无损的图像压缩标准,这样就可以比无损JPEG压缩效率更好。它能够得以发展是因为基于哈弗曼编码的无损JPEG压缩或者其他压缩算法其压缩效果不理想,且在刚开始时无法做到完全去相关性.JPEG-LS,在去相关性上表现的较为良好,该标准的第一部分是在1999年 (T.87)完成的,第二部分是在2003 (T.870)对外公开的,且引入了算法编码。JPEG-LS的核心是LOCO-I算法,预测,建立误差模型,基于上下文误差编码是该算法的核心所在。这些低复杂度的算法模型是基于假设预测误差遵守双边几何分布(或者称为离散拉普拉斯分布)且使用类似于Golomb的编码方式(该方式对于几何分布编码效果较好)。除了无损压缩,JPEG-LS也有近无损压缩,该近无损压缩的最大误差值可以由编码段控制。JPEG-LS压缩在速度上比JPEG 2000快的多,且效果比无损的JPEG标准压缩要好的多。
无损压缩包含两个独立过程: 建立模型 和 编码.
把像素按照某种方式按照时间方式处理成为一维数据  ,希望通过假定的条件概率分布
,希望通过假定的条件概率分布
 推断
推断  .
.
在新的无损压缩算法里,概率的分配被分为三项工作:
- 通过
 的一个子集给出
的一个子集给出  的一个预测
的一个预测
- 确定
 的上下文,通常为
的上下文,通常为 的一个子集的一个函数
的一个子集的一个函数 - 给出上下文预测误差
 的概率模型
的概率模型
1.预测流程
2.上下文模型
- 编码分布
- 上下文确定
3.编码
- Golomb-Rice编码
- 序列参数估计
- 偏差删除
4.嵌入字母表扩展
1.对于上下左右边缘都不存在时:
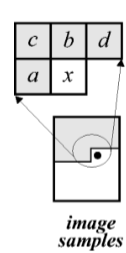

 就是这三个数字
就是这三个数字  的中位数.
的中位数.
2.对于左边缘不存在时:
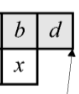
对于左边缘不存在的情况,选择  .
.
3.对于上边缘不存在时:
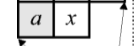
对于上边缘不存在的情况,选择  .
.
上下文模型中,关键的目标是减少参数的数量,以避免参数的稀释作用.
先验知识: 一般认为,连续色调图像的预测目标近似的服从拉普拉斯分布.
TSGD model:a two-sided geometric distribution model(双侧的几何分布,也就是拉普拉斯分布)
对于预测误差  ,偏移参数
,偏移参数  表示为整数部分与小数部分的差有
表示为整数部分与小数部分的差有
 有概率密度函数
有概率密度函数  :
:

其中  ,R称为整数自适应项.
,R称为整数自适应项.
特别的对于R=0的情况:

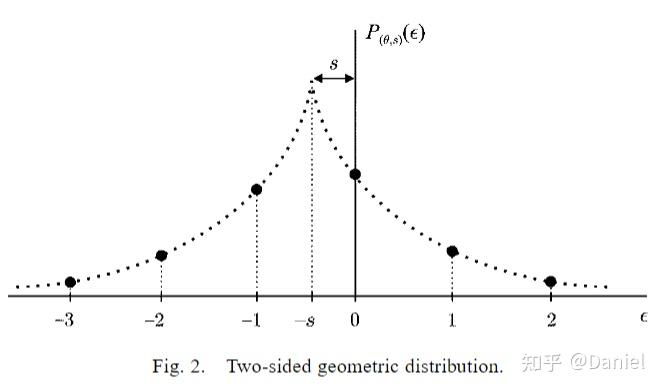
下面讨论误差  的范围:
的范围:
对于预测值  ,由于
,由于  是比特数.
是比特数.
两边减去  ,得到
,得到  .
.
可以认为  ,这个式子后面有大用.
,这个式子后面有大用.
在实际应用中,由于  比较大,所以把
比较大,所以把  看作无界的.
看作无界的.
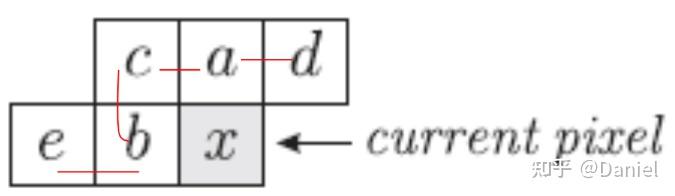
这是jpeg-ls官方文件定义的上下文.
可以计算几个差值

记  为量化得到的相应区间,由于环绕x的对称性,可以假设
为量化得到的相应区间,由于环绕x的对称性,可以假设
 的可能区域有
的可能区域有  个,在官方文件中取得是
个,在官方文件中取得是  ,对应的9个区间为
,对应的9个区间为

 的可能区域为
的可能区域为  个,在官方文件中取
个,在官方文件中取  ,对应的3个区间为
,对应的3个区间为

为什么q4对应的区间稀疏那么多呢?这是因为像素b和e距离x比较远,所以T一般远小于R.
这样,对像素x来说就有了  个可能上下文个数了,但是再考虑对称性
个可能上下文个数了,但是再考虑对称性

所以上下文的可能个数减半,变成  .
.
这样像素x就有  个上下文,事实上官方说,可以有的时候省略掉q4,因为b和e距离x比较远,这样所有可能的上下文个数变成了
个上下文,事实上官方说,可以有的时候省略掉q4,因为b和e距离x比较远,这样所有可能的上下文个数变成了  .
.
一元编码(Unary coding)是一种简单的只能对非负整数进行编码的方法,对于任意非负整数num,它的一元编码就是num个1后面紧跟着一个0,或者num个0后面紧跟着一个1,具体哪种情况需要协议的约定,如无特殊约定,一般默认使用第一种。

对于正整数m,非负整数n可以使用Golomb编码进行表示,符号记作  ,用小学就学过的带余除法,
,用小学就学过的带余除法,
非负整数n可以使用Golomb编码表示为以下两部分拼在一起
 的二进制表示
的二进制表示![\left[\frac{n}{m}\right]](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg) 的一元码表示
的一元码表示
显然,当m较小时,Golomb编码码长开始很短,但随着n增长,码长迅速增加;这适用于0出现的概率p较小的游程编码,即只有很少的长游程。当m较大时,Golomb编码的初始码长较长(对于n=1,2…),但是随着n增长,其码长增加速度较慢;这适用于0出现的概率p较大的游程编码,即存在较多的长游程。
m的选择
容易知道Golomb编码对于分布
 的时候是最优的.
的时候是最优的.
所以**的m取决于p,当平均编码长度最短,可以证明其是最接近  的整数,即其值满足以下条件:
的整数,即其值满足以下条件:

更进一步,可以获得**的m的值为

Golomb-Rice编码是Golomb编码的特殊形式,被除数m的取值为  .
.
所以正整数n的Golomb-Rice编码为把n表示为二进制的 1至k位 与 的一元码表示.
的一元码表示.
该编码方式记为  .
.
所以  的码长为
的码长为 ![k+1+\left[ \frac{n}{2^k} \right]](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg) .
.
我们要编码的对象为预测误差,它是可正可负的
取变换 
得到范围 
如果  服从以0为中心的拉普拉斯分布,则
服从以0为中心的拉普拉斯分布,则  近似的服从几何分布,这就是为什么要使用Golomb-Rice编码,因为Golomb-Rice编码对几何分布是最优的.
近似的服从几何分布,这就是为什么要使用Golomb-Rice编码,因为Golomb-Rice编码对几何分布是最优的.
LOCO-I算法是这样估计k的:在估计  的基础上估计k.
的基础上估计k.
 的概率密度函数为
的概率密度函数为  为了取值的和为一.
为了取值的和为一.
数学期望是: 
所以对于k的较好估计为 ![\left[ \log_2 \mathbb{E}(|\epsilon|)\right]+1.](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg)

- N,上下文出现的个数
- B,上下文累积误差(+C之后)
- C,纠正值,用来加在
 上,C的初始值为0,修正后误差的均值
上,C的初始值为0,修正后误差的均值  的时候增加,
的时候增加,  的时候减少,这样会使得平均误差偏差趋于
的时候减少,这样会使得平均误差偏差趋于 ![\left[ -0.5,0.5 \right]](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg) .
.
Golomb-Rice编码对于理论编码位数小于1的符号,编码效率不高(平均码长大于理论值).
LOCO-I算法给出的解决方案是在上下文条件中嵌入字母表扩展.
之后我们可以距离了解JPEG-LS Baseline的工作原理.
上一篇文章中我们了解JPEG图像的基础知识,以及核心的几个步骤,接下来,我们针对源码深入学习一下相关原理,废话不多说,直接开始。
Fenngtun:音视频编解码–JPEG格式介绍JPEG官网推荐了两个多媒体开源库,如下链接:
https://jpeg.org/jpeg/software.html
libjpeg-turbo 是一种 JPEG 图像编解码器,它使用 SIMD 指令(MMX、SSE2、NEON、AltiVec)在 x86、x86-64、ARM 和 PowerPC 系统上加速基线 JPEG 压缩和解压缩。在此类系统上,libjpeg-turbo 通常是 libjpeg 的 2-6 倍,其他条件相同。在其他类型的系统上,libjpeg-turbo 凭借其高度优化的霍夫曼编码例程,仍然可以在很大程度上胜过 libjpeg。在许多情况下,libjpeg-turbo 的性能可与专有的高速 JPEG 编解码器媲美。
libjpeg-turbo 实现了传统的 libjpeg API 以及功能较弱但更直接的 TurboJPEG API。libjpeg-turbo 还具有色彩空间扩展功能,允许它从/解压缩到 32 位和大端像素缓冲区(RGBX、XBGR 等),以及一个全功能的 Java 接口。
- 在 x86、x86-64 和 ARM 平台上,速度是 libjpeg 的 2-6 倍
为流行的 Linux 发行版、Windows、OS X 和 iOS 提供的 32 位和 64 位二进制文件- 可用于 GPL 和专有应用程序
- 提供行业标准的 libjpeg API/ABI(可以模拟 libjpeg v6b、v7 或 v8,尽管 libjpeg-turbo 不支持 libjpeg v8 中引入的非标准 SmartScale 格式)
- 提供 VirtualGL 和 TurboVNC 使用的 TurboJPEG API
- 与商业/闭源加速 JPEG 编解码器的性能相似
- 功能齐全的 Java 包装器
因此JPEG代码走读以 libjpeg-turbo为例,其基本调用流程在libjpeg-turbo-main\example.c 中给出明确实例:
- 初始化压缩对象jpeg_create_compress;
- 设置压缩后的数据的输出形式jpeg_stdio_dest,比如输出到文件设置压缩的参数jpeg_set_defaults。 这里最重要,也就是我们需要把optimize_coding设置为true。 因为默认是false。
- 开始压缩jpeg_start_compress;
- 按行循环写入,jpeg_write_scanlines;
结束压缩,jpeg_finish_compress;
释放压缩对象。
jpeg_destroy_compress
https://www.jianshu.com/p/20902ca448ae?utm_source=oschina-app
https://blog.csdn.net/ta71/article/details/
https://glumes.com/post/opengl/libjpeg-turbo-compile-and-practice/
接下来我们继续深入函数内部了解其相关实
jpeg_create_compress 做了一次宏定义:
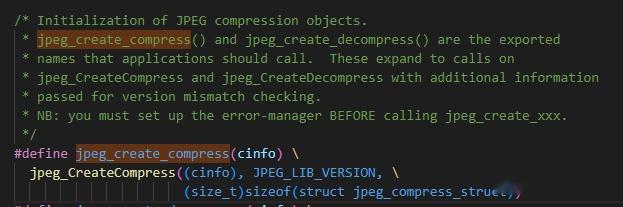
目录:libjpeg-turbo-main\jcapimin.c,主要作用:JPEG 压缩对象的初始化。
设置JPEG编码器的输出目标,即将编码后的图像数据写入文件。具体实现是通过定义一个名为jpeg_stdio_dest的函数,并传入一个指向已打开的文件的指针作为参数。
依据cinfo->dest是否为空决定是否重新alloc一段内存,其目的就是为了不用多次执行jpeg_stdio_dest。
在设置完目标位置之后,代码接着将dest指针转化为my_dest_ptr类型,并设置其结构体的三个函数指针:init_destination、empty_output_buffer和term_destination,它们分别表示初始化目标位置、清空输出缓存和结束输出操作。
最后,将outfile指针保存到my_dest_ptr结构体的outfile字段中,以备后续写入数据时使用。
设置压缩所需要的默认参数集,

第一,会检查cinfo->global_state的值是否为CSTATE_START,如果不是,则会通过ERREXIT1函数发出一个错误消息(JERR_BAD_STATE)。

第二,如果write_all_tables为真,则会将所有的表标记为要写入。
第三,该函数会调用cinfo->err->reset_error_mgr函数和cinfo->dest->init_destination函数来重新初始化错误管理器和目标模块。
第四,通过调用jinit_compress_master函数,选择并初始化所有必要的压缩模块。
第五,调用cinfo->master->prepare_for_pass函数来设置第一遍扫描的参数和状态。
最后,将cinfo->next_scanline设置为0,表示还没有扫描过任何扫描线,将cinfo->global_state设置为CSTATE_RAW_OK或CSTATE_SCANNING,表示已经准备好开始第一遍压缩操作了。
将一些扫描行的数据写入到JPEG压缩器中,函数的返回值是实际写入的行数。如果写入的行数小于提供的num_lines,则只有在数据目标模块请求暂停压缩器的情况下才会发生;或者如果传递了超过图像高度的扫描线数。
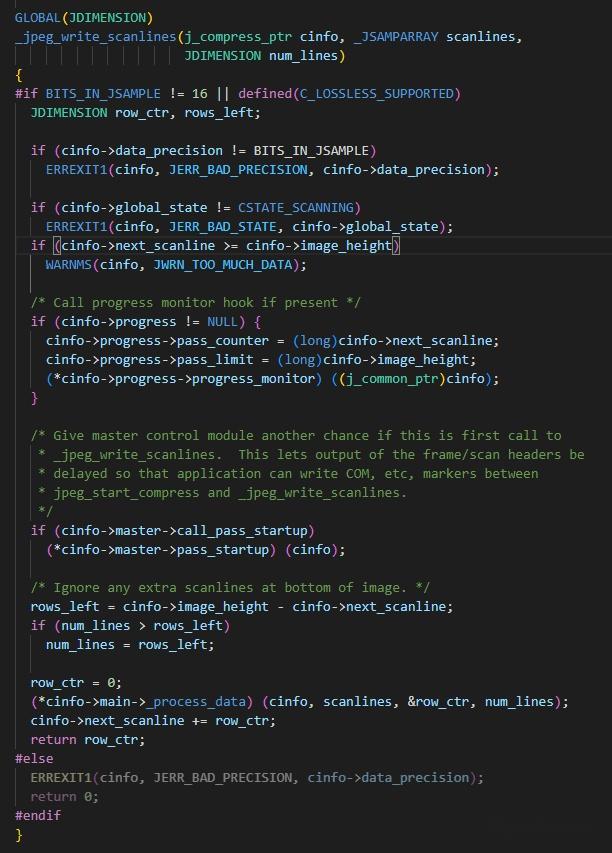
jpeg_finish_compress完成JPEG压缩操作。如果选择了多通道操作模式,则可能需要进行大量的工作,包括实际输出的大部分内容。
第一,会根据global_state进行不同模式判断,判断压缩状态并终止第一次遍历(pass),如果需要进行更多的遍历,则执行它们,最后写入文件尾并清理资源。
第二,执行pass判断,调用 cinfo->master->prepare_for_pass(),准备进行下一轮压缩。并依据位深精度不同,分别调用compress_data接口
第三,完成一些必要的清理工作:调用了标记处理模块(marker)中的函数,用于在图像流的结尾写入EOI(End of Image)标记,并完成一些与标记相关的清理工作;调用了目标数据源(destination)中的函数,用于完成输出图像的最终写入操作;调用了jpeg_abort函数,释放内存并重置全局状态。
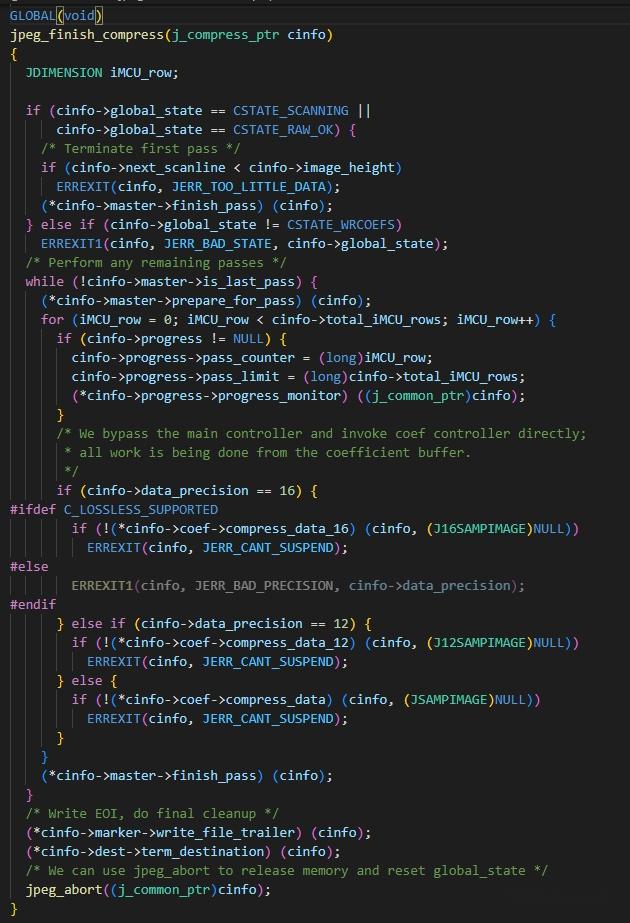
JPEG压缩器销毁函数jpeg_destroy_compress,它调用了通用的jpeg_destroy函数来销毁压缩器对象cinfo。通用的jpeg_destroy函数会释放该对象所使用的所有资源,并将对象本身的内存也释放掉。
我是一枚爱跑步的程序猿,维护公众号和知乎专栏《MediaStack》,有兴趣可以关注,一起学习音视频知识,时不时分享实战经验。
adobe家族陆续更新到2024版,Lightroom也支持了导出为JPEG XL和AVIF两种先进图片格式。为了考察这两种图片在工作流的可用性,做了简单测试。
1.将143张延时序列raw文件从Lightroom导出为各种格式图片(分辨率统一为3840x2560), 对比文件大小,导出花费时长。
2.将导出的各种格式的图片序列分别用FFMPEG编码为视频。比较兼容情况,编码速度。编码参数为 ffmpeg.exe -f image2 -r 25 -i %%04d.JXL -vf “zscale=m=709, format=yuv420p10le” -vcodec libx265 -crf 9
3.在图片查看、管理软件中确认JPEG XL和AVIF的兼容性。
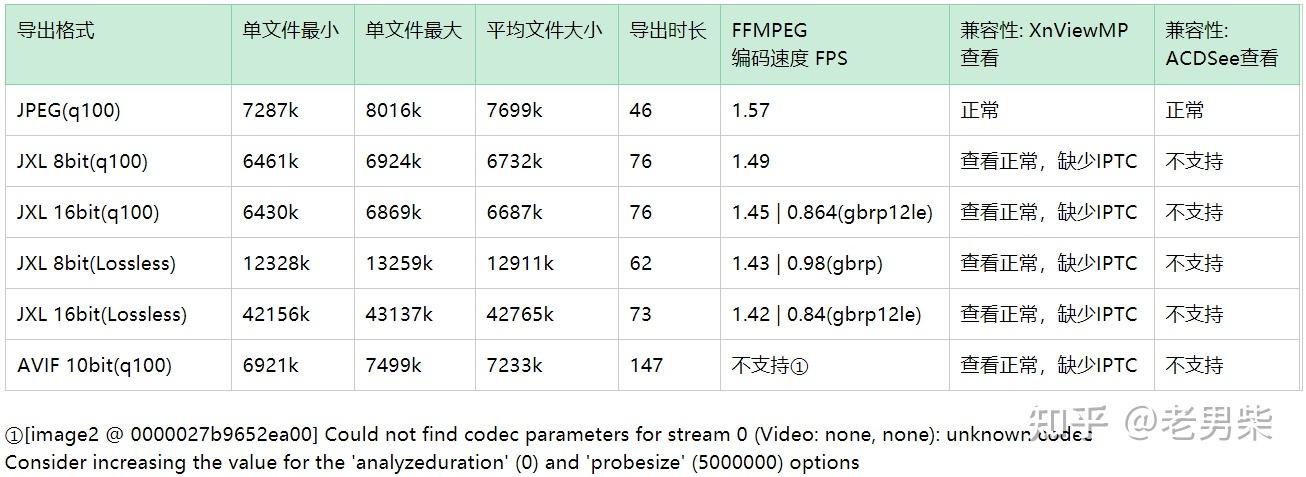
结论:
1.JPEG XL和AVIF在有损编码下,都用最高质量导出,体积都小于JPEG。特别是JPEG XL使用16bit精度时并不会增加体积。这一点令人兴奋。
2.JPEG XL在之前不少文章中说到无损压缩的压缩率较强,但经过我的对比,发现比png只小一点点而已,10%不到,无论8bit还是16bit下。
3.兼容性则令人沮丧。我用来管理图片的ACDSee即使是刚出的2024版也无法显示这两种图片。偶尔用一下的XnViewMP(v1.6.1)倒是能够正常显示图像,但缺少IPTC元数据。Lightroom在导出为avif和jxl时会提示这样将丢失元数据。暂时不知道IPTC的支持问题是Lightroom还是这两种格式自身的原因。不管怎么说,这对于依赖IPTC来管理图片的人来说是不可接受的。
对于使用苹果手机的用户来说,HEIC格式相信是再熟悉不过了。HEIC其实早在2015年就有了,只是2017年IOS将其作为默认的图片格式之后,才为大家所熟知。
作为苹果2017年才刚开始推行的图片格式,肯定会出现兼容性的问题。明明在手机上可以打开,但是在电脑上或者传到其他地方就不行了。
于是大家慢慢习惯于,将HEIC格式的图片转换成JPG或其他格式的图片。但实话说,我们并不建议你这样做。
为什么呢?

HEIC使用的是“高效图像格式(High Efficiency Image Format)”来保存照片,
JPEG 则是联合图像专家组(Joint Photographic Experts Group)的简称,主要借助彩色像素来存储照片。
JPEG之所以被广为使用,主要是因为其可以将图像压缩成非常小的文件。因此当年在制作网站时,前端人员会倾向于使用这种格式。
但事实上,现在的一些图片格式在图片大小上已经能做到比JPEG更小,且质量更高、压缩更少,HEIC就是其中之一(谷歌的WEBP也是)
不妨从压缩程度、存储大小、图片质量、兼容性等4个角度来看
压缩:你应该知道JPEG提供的是一种“有损压缩”,不过你可能不知道的是,事实上你每一次的编辑和保存JPEG格式图片时,都会损失一些背景数据,从而影响图片质量(虽然你可能看不出来,但对于设计来说影响是很大的)
而HEIC则可以在不影响质量的前提下,将图像分解成更小的文件。
注意,并不是说HEIC就是无损格式的,它同样是有损格式,但是图像质量更好,另外这种格式是可以储存编辑信息的,这样就可以确保将来有需要的时候对已经编辑的图像做还原。
存储大小:相比JPEG,HEIC的存储占用要小很多,差不多可以节省一半以上的空间。
比如一张JPEG要10MB的图片,用HEIC储存只需要5MB,当然你可能会说10MB对于现在的手机来说算什么?!
其实还真算个大问题,手机存储焦虑几乎是现在手机的头号问题,毕竟谁的手机里不是存着几百、上千甚至上万张照片的,这时候节省一半的空间可是个很大的数字!
而且,万一你需要进行备份或者传输,比如因为手机空间不够要把照片备份到Me盒之类的私有云设备里,那么HEIC可以大大加快整个备份传输的速度,节省时间。

图像质量:这一点上HEIC同样更优秀,透明度以及更宽的动态范围让HEIC格式的图片质量要优于JEPG
兼容性:这点毋庸置疑是JPEG更好,而且是“完爆”,基本上所有的设备都会支持JPEG,但是HEIC则基本上主要是在苹果的设备上,另外etsme的产品也都支持HEIC格式。
综上来看,除了兼容性,其他任何方面HEIC都要好于JPEG,所以不妨就把照片用HEIC格式存着。
当然,也不能忽视兼容性的问题,毕竟这是个“一白遮百丑”的大问题。解决的办法无非两类:
使用支持HEIC格式的软件打开照片,或者将HEIC转换成JPEG
首先是苹果全家桶,这个是自然的……不管是Mac还是IOS都支持HEIF
如果是Windows,在Win10的18.09版本之后都已经支持HEIC格式了,只需要在Microsoft Store里搜索“HEIF图像扩展”,下载安装后就可以打开HEIC格式的照片了。
P.S.Win11开始已经默认内置HEIF扩展了
安卓10之后的版本也开始支持HEIF,Ubuntu则是在20.04之后的版本开始支持

如果你的设备不是以上操作系统的版本,或者实在想要将HEIC转换成JPEG的格式。
那么大概有以下几种方法
苹果当然知道HEIC的兼容性问题,所以提供了“在通过USB将文件传输到Win10时自动转换格式”的功能
打开【设置】——【照片】——传输到PC或Mac这里,选择“自动”
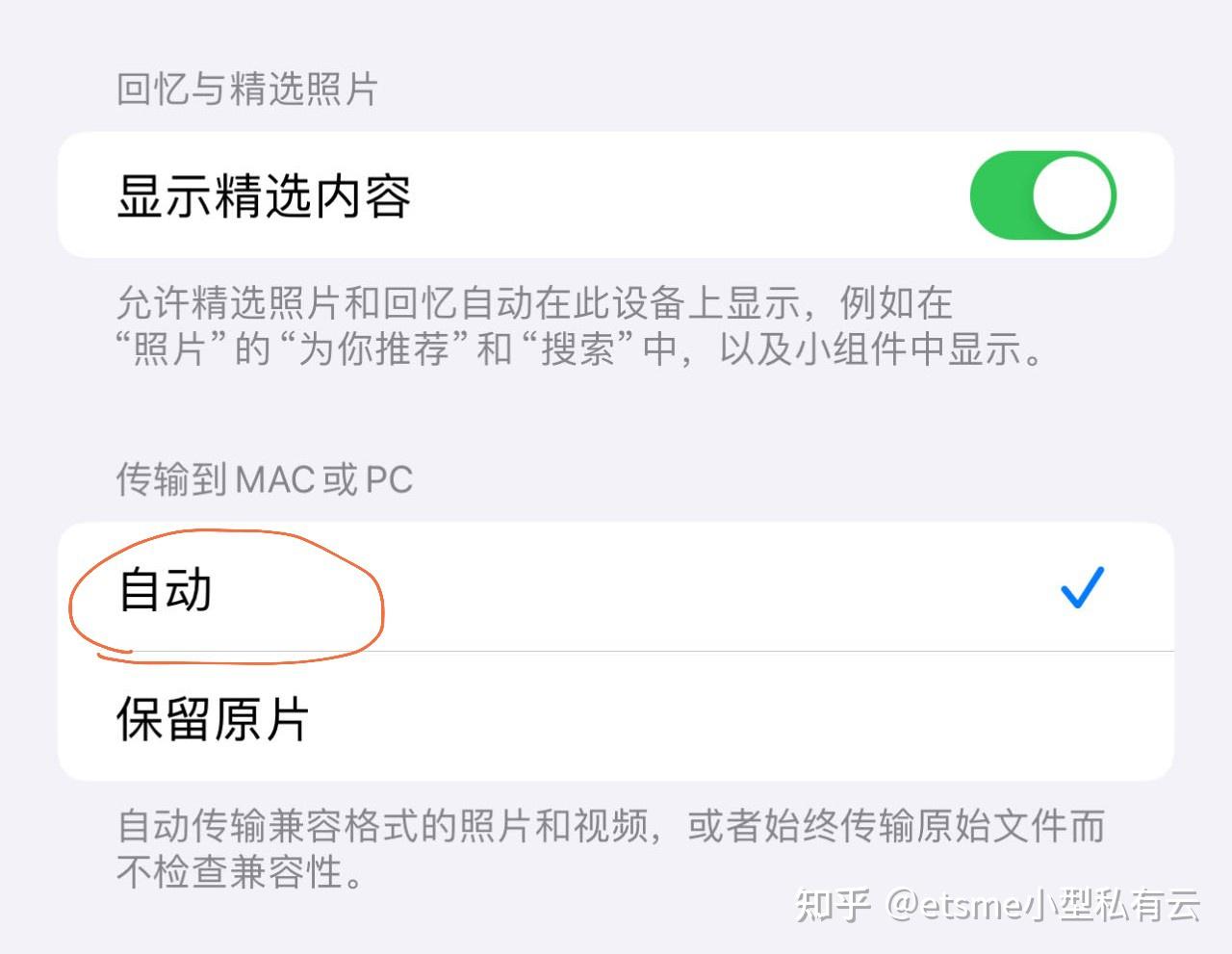
这种方式有几个缺点,一个是你得通过USB传输,另一个是听说这种方式传输经常会出现一些问题导致传输失败……
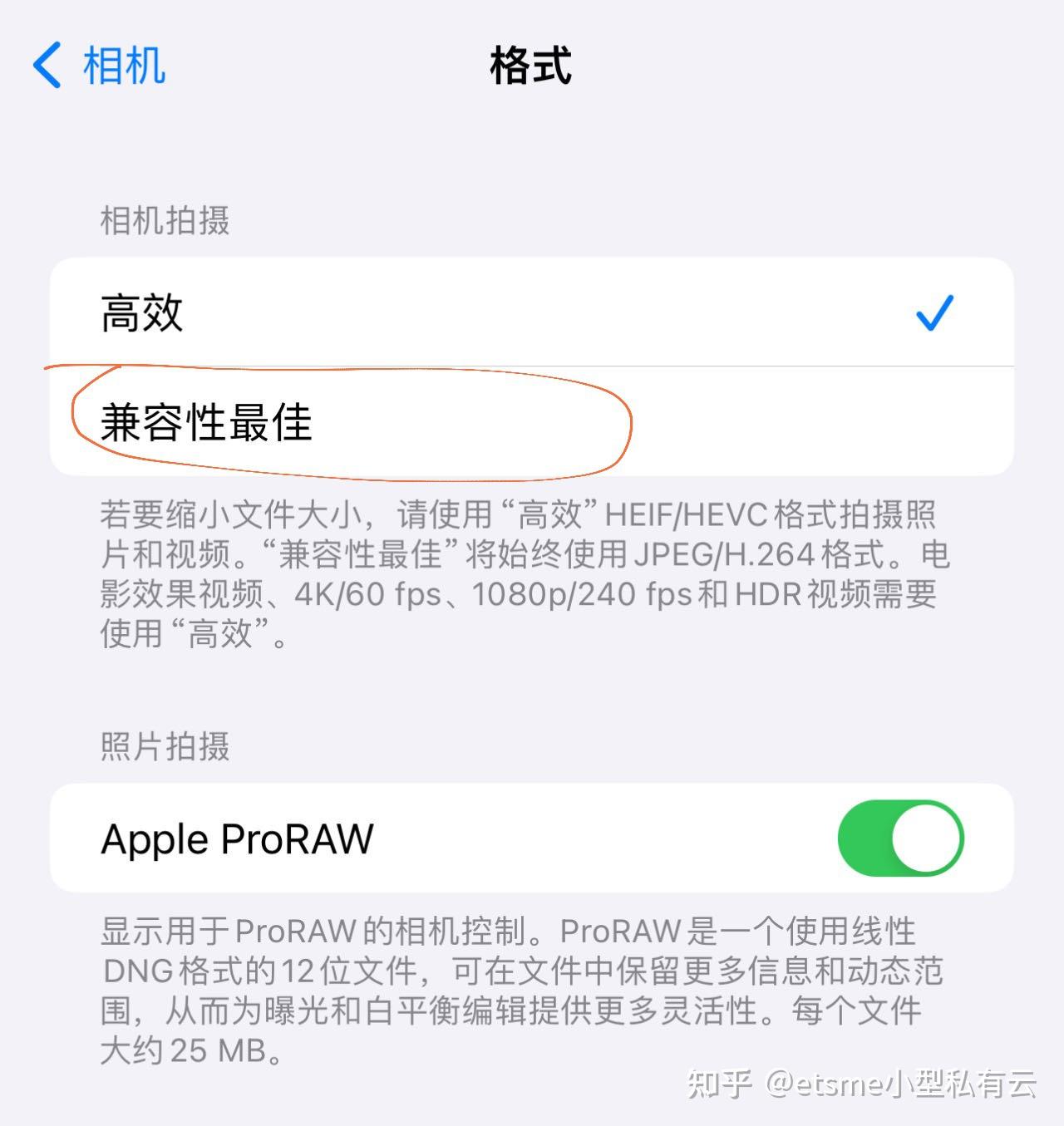
还有一种方式是,直接在苹果手机中关闭HEIC格式保存,直接用JPEG替代
方法是【设置】——【相机】——【格式】,然后选择“兼容性**”
有很多第三方的软件可以提供转换功能,比如iMazing HEIC Converter、HEIC Converter Free……
或者你也可以自己网上搜一下其他的软件,不过…千万注意,小心那些流氓软件和恶意广告。
有一些网站也会提供自动转换的功能,只要把照片上传上去就可以了。
还有一些网盘应用OneDrive、Dropbox等,或者大家常用的钉钉、微信都会在你上传HEIC文件时,自动转换成JPEG。
不过,老实说,我们并不建议你用最后的这种方法,在线传输的方式进行的转化,本质上都是将照片先上传到对方的服务器,也就是我们常说的公有云。
在服务器上处理好之后,再提供下载,也就是说服务器上一定会有存你上传的照片。
虽然一般来说,网站或网盘等服务都会有严格的隐私协议不动用户的数据,但用户数据泄露之类的事情终究还是偶尔能听到。
所以,如果是非常隐私或者非常重要的照片,不建议通过在线的方式进行转化。
另外,还是最开始的话,鉴于HEIC格式的种种好处,直接不转换成JPEG或许是更好的选择。
如果是要做图片处理,PS等软件是已经支持HEIC格式的,从大的趋势上也可以发现,目前越来越多的操作系统开始内置HEIC扩展。
未来很有可能会有越来越多的厂家默认使用HEIC格式作为照片的存储。
那这就引出了一个新的问题,如果不转化格式,我如何原汁原味的保存HEIC格式文件呢?
毕竟,网盘之类的工具都是自动转换格式的,每次都用USB传输又比较麻烦。
这里提供的一个解决方法是——通过etsme Me盒。
Me盒是一个小型私有云,将它摆在家里通电、联网后,就相当于你有了一个自己的小型云服务器(你可以暂且理解为网盘)。

然后,你就可以通过Me盒APP来将各个终端中的数据相互传输。
苹果手机里的HEIC文件当然也可以,而且是原汁原味100%保真的保存,不会压缩、不会改变格式。
另外,非常方便的一个点是,Me盒的“手机自动备份”功能就可以直接识别HEIC文件并自动保存,这样就不需要一个个手动勾选了。
想要把照片放到其他设备上,只要在其他设备上打开Me盒APP,再下载到本地就可以了。
通过本文,相信你应该已经了解了HEIC相比JPEG格式来说拥有很多的好处,虽然其兼容性上还远不如JPEG,但已经有越来越多的操作系统开始默认支持HEIC格式。
即便设备本身不支持,你也可以通过下载“支持HEIC格式的软件”来打开它。如果一定要将HEIC转换成JPEG格式,方法也有很多。
但如果是重要、隐私的数据,不建议通过上传公有云的方式来进行转换。
最后,作为一个未来有巨大潜力的图片格式,强烈建议你从现在开始就接受它,如果需要跨设备传输HEIC文件,请务必选择像Me盒这样能100%保真的工具,而不是使用自动会将其转换为JPEG格式的工具。
HEIC节省存储空间、高画质、可恢复编辑等一系列的特性都会给你带来巨大的好处。
我是 @etsme小型私有云 ,记得关注、评论和点赞哦~
etsme个人/小型私有云_小型云计算_家庭云存储_一体化设备-etsme官网etsme京东商城etsme官方小程序商城之前一直很好奇图片和视频是如何压缩的,由于视频格式会更复杂,所以先从JPEG下手
因为网上资料太难找太分散,有些又看不太懂,所以根据自己的理解整理了一下
JPEG(Joint Photographic Experts Group),全称为联合图像专家小组,同时也是我们生活中很常见的一种图像格式,一般以.jpg作扩展名。JPEG采用了多种方法来对图像进行有损压缩,从而使得观感相差不大的情况下减小了较多的文件体积
常见的JPEG图像数据按照如下流程进行压缩:
JPEG中会首先对图像以8x8的块为单位划分,不足8x8的会填充剩余部分。不过具体填充什么我没研究过,但是解码显示出来的时候会忽略掉这部分,所以应该是无所谓的。
对图像进行8x8分块也是为了方便下一步进行DCT变化
DCT(Discrete Cosine Transform,离散余弦变换)是一种把数据从时域转化到频域的数学方法,把图像数据转换到频域之后,我们就可以从中分离出各种频率的信息。
DCT变换过后数据按照不同频率进行划分,得到的数据实际上是不同频率余弦波的系数,把这些系数乘上对应频率的余弦函数就能得到原来的数据
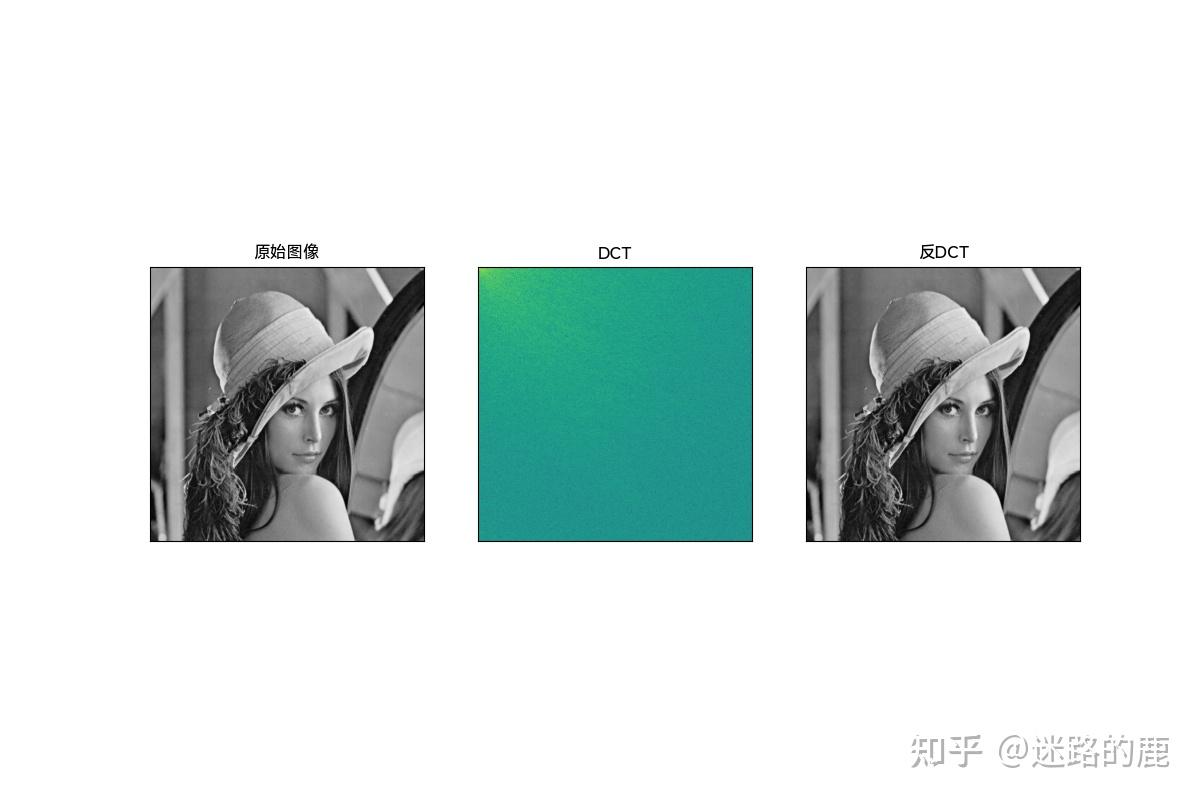
但要注意的是DCT变换过后数据的大小也不会发生改变,相当于把数据用另一种方式表示,就好像同一句话你用普通话和方言讲出来就是两种表达方式。
DCT变换后我们就能区分不同频率的信息了,其中高频信息是图像中的一些细节,将变换后的高频部分系数置0则可以去除这些细节。因为人眼对高频信息不是很敏感,所以观感差距不会很大,就像你有轻度的近视,但不影响你看清一个物体。
比如下图

我们会发现,假如只保留DCT变换后左上角的低频部分,还原出来的图像其实和原图差距不大;而如果看保留高频后还原出来的图像,仔细看会发现只留下了物体边缘等细节部分的一些痕迹(也就是高频部分)
此时选择去除哪些频率的信息就成了关键点,我们要给图片选择一个“近视程度”来让减少高频信息。好在JPEG标准已经准备好了几种量化表,对应了不同的图像质量,我们只需要把DCT变换后的数据除以量化表中的对应项就完成了量化操作。
对数据进行过量化之后仍然没有减小体积,因为去除的高频系数只是被替换成了0,占用的空间还是不变,这时候就轮到Z字形扫描(Zig-Zag Scan)出场了。
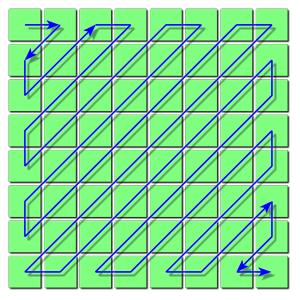
Z字形扫描就如同字面意思一样,按照上图顺序重新排序顺序。因为高频信息聚集在右下角,按照这种方式扫描后就可以把被替换成0的高频系数连续排列了
顺带一提,知名音视频编解码工具FFmpeg的图标就来源于Z字形扫描

什么是DC系数和AC系数?
简单地说, DC系数就是一个块中第一个数,而 AC系数就是剩余的数
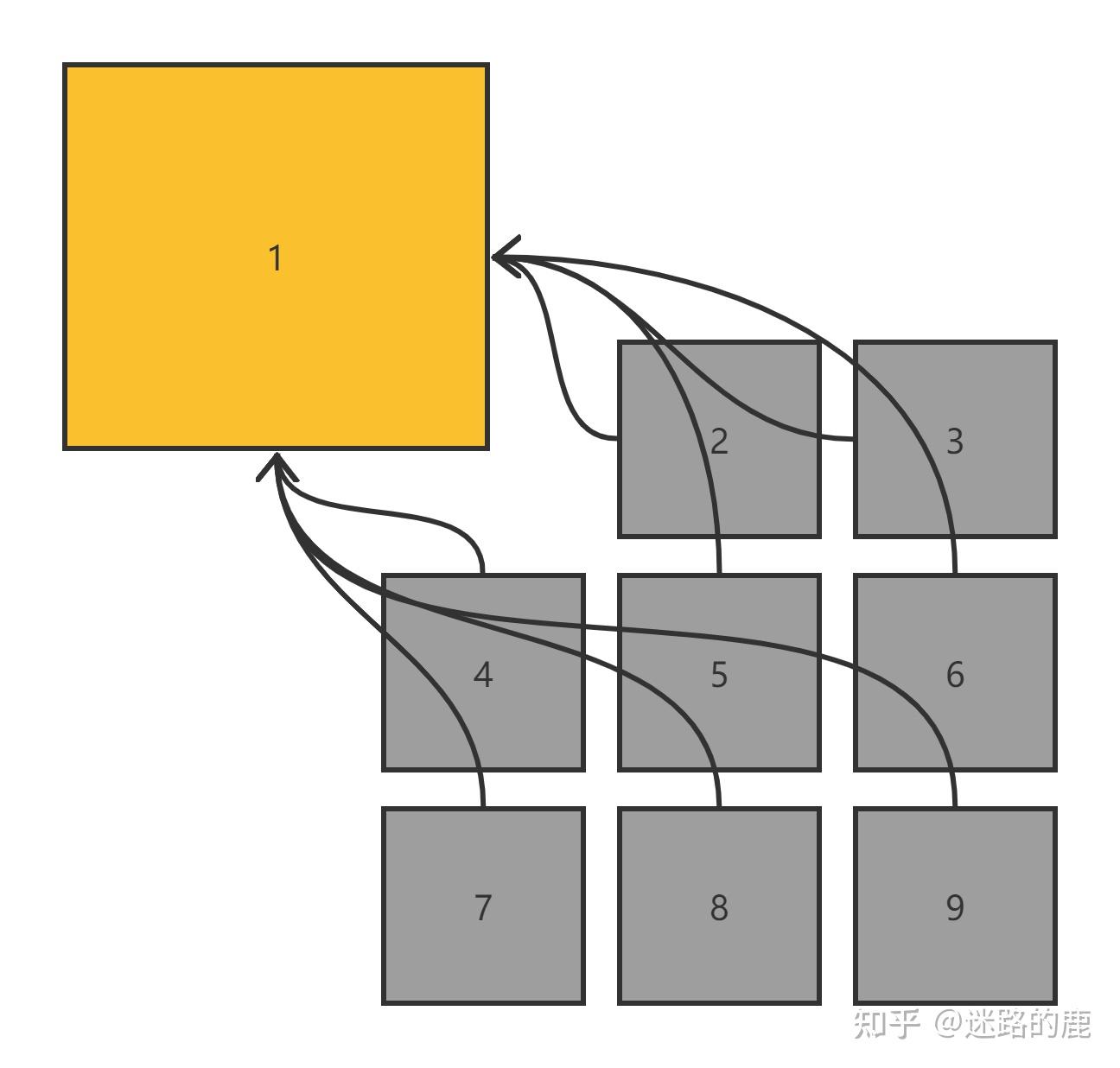
前面的Z字形扫描完成了准备操作,真正压缩则是交给游程编码(Run Length Encode, RLE)
游程编码以两个数为一组,第一个数表示第二个数的重复次数,对于压缩经过Z字形扫描过后,存在大量连续的0的数据来说再合适不过了
假如直接舍弃后面一半的信息,对画质影响不大的情况下,减少了差不多一半的数据量!
对于DC系数,采用的是一种叫差分脉冲编码调制(Differential Pulse code modulation,DPCM)的编码方式
听起来很高深,实际上就是把DC系数换成这一个块和上一个块的DC系数的差值。比如上一个块的DC系数是20,这一个块的DC系数是10,那就写入-10。如果是第一个块,那就不用变(或者也可以看作前面有一个不存在的DC系数为0)。
JPEG中DC系数和AC系数的存储格式:
在实际存储的数据中,一个系数分成两部分
第一部分长度为一个byte。
对于AC系数来说采用了游程编码,低四位表示第二部分的长度(以bit为单位),高四位表示这一数据前0的个数; 对于DC系数来说这一整个byte就表示第二部分数据的长度(也是以bit为单位)
第二部分的第1位是符号位,0表示负数,1表示正数。如果是正数,无需处理;如果是负数,则是对原数包括符号位在内的每一位取反的结果
最后是对所有的数据进行熵编码,一般用的是范式霍夫曼编码(Canonical Huffman Code)。
范式霍夫曼编码基于霍夫曼编码,霍夫曼编码核心思想是为出现频率更高的数据分配更短的编号,为出现频率低的数据分配更长的编号,这样就可以实现无损压缩数据。而由于霍夫曼编码以bit为单位,长度又不确定,读取时无法区分,所以采用了范式霍夫曼编码。
JPEG中范式霍夫曼编码的存储格式:
首先用一个大小为16个字节的数组存储编码后数据中对应长度为1bit~16bit的原始数据的种类数,后面按同样的顺序紧跟所有种类的原始数据
而编码后的数据要通过如下方式得到:
数从长度为1bit的0开始,长度相同时每编码一个数就+1,长度每增加1bit就要左移1位
当然,JPEG标准中也给出了参考的范式霍夫曼编码的对照表
JPEG解码系列博客:多媒体-编解码 - 随笔分类 - OnlyTime_唯有时光 - 博客园 (cnblogs.com)
JPEG标准:Microsoft Word - T081E.DOC (w3.org)
白话文理解DCT离散余弦变换 - 乂墨EMO - 博客园 (cnblogs.com)
一个Rust写的JPEG解码器:MROS/jpeg_tutorial: 跟我寫 JPEG 解碼器 (Write a JPEG decoder with me) (github.com)
我学习过程中写的JPEG图片查看器:Ryan1202/my-tiny-jpeg-viewer: A Tiny Jpeg Viewer (github.com)
下一章:JPEG格式研究——(2)JPEG文件格式 - 知乎 (zhihu.com)
JPEG文件除了图像数据之外,还保存了与图片相关的各种信息,这些信息通过不同类型的TAG存储在文件中。
JPEG通过TAG标记压缩书记之外的信息。所有的TAG都包含一个TAG类型,TAG类型大小为两个字节,位于一个TAG的最前面。TAG类型的第一个字节一定为0xFF
以下是部分常见的TAG类型
| TAG类型 | 数值 | 备注 |
|---|---|---|
| SOF0 ~ SOF3 SOF5 ~ SOF7 SOF8 ~ SOF11 SOF13 ~ SOF15 |
FF C0 ~ FF C3 FF C5 \Lh~ FF C7 FF C8 ~ FF CB FF CD ~ FF CF |
不同的编码模式对应不同的SOF,详见JPEG标准Table B.1。本文以常见的SOF0为研究对象 |
| DHT | FF C4 | Define Huffman table(s),定义了解码所需的哈夫曼表 |
| RSTm | FF D0 ~ FF D7 | 遇到时重置DC系数,数字会递增,具体含义不清楚 |
| SOI | FF D8 | Start of Image,表示图像文件的开始 |
| EOI | FF D9 | End of Image,表示图像文件结束 |
| SOS | FF DA | Start of scan,表示这一个TAG后就是压缩的图像数据,记录了DHT、DQT与图像不同部分的对应关系 |
| DQT | FF DB | Define quantization table(s),定义了解码所需的量化表 |
| APP0 ~ APP15 | FF E0 ~ FF EF | 应用保存的图片相关信息(如相机信息等) |
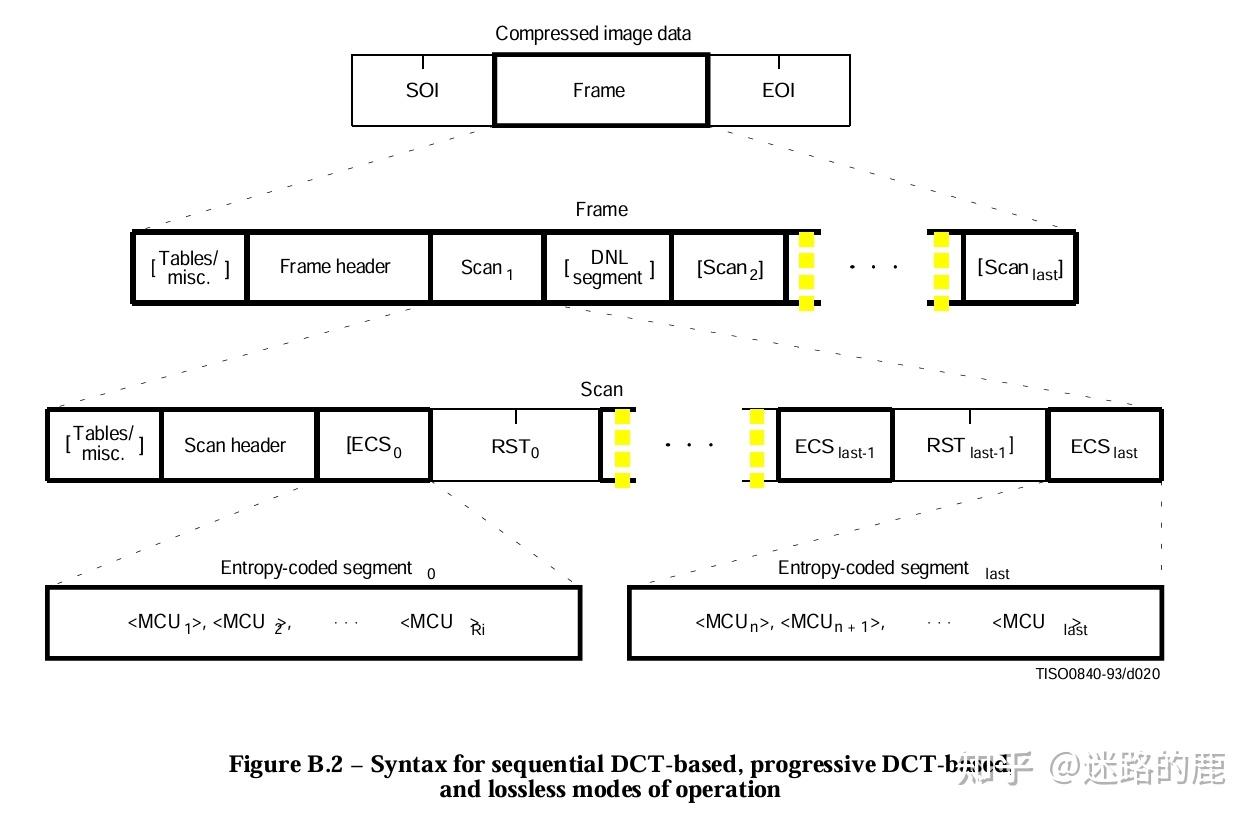
压缩数据中也是存在TAG的,虽然大部分TAG都在文件开头,但是也有少部分是例外。如EOI就在文件的末尾,RSTm会出现在压缩数据当中。
那么问题来了,如果压缩数据中有一个字节本身就是0xFF怎么办?JPEG的做法是在0xFF后面再加一个字节0x00,用于表示这不是一个TAG。
因为不知道解码需要哪些TAG,我在尝试写JPEG解码器的时候耗费了大量的时间在研究TAG上。总结出对于常见的JPEG图片解码需要的TAG:
1.SOI和EOI:用于确定文件的开头和结尾
2.DQT和DHT:保存了解码时需要用到的哈夫曼表和量化表
3.SOS:保存了图片不同部分的需要用哪个哈夫曼表
4.SOF:图片的长和宽、采样精度等、使用哪个量化表都保存在SOF中
5.RST:部分图片存在RST,遇到RST时要重置DC系数才能得到正确的图像
这里有个小坑,我原先一直以为DQT和DHT都是一个TAG对应一个表,后来发现一个TAG可以不只一个表
哈夫曼表的存储格式如下:
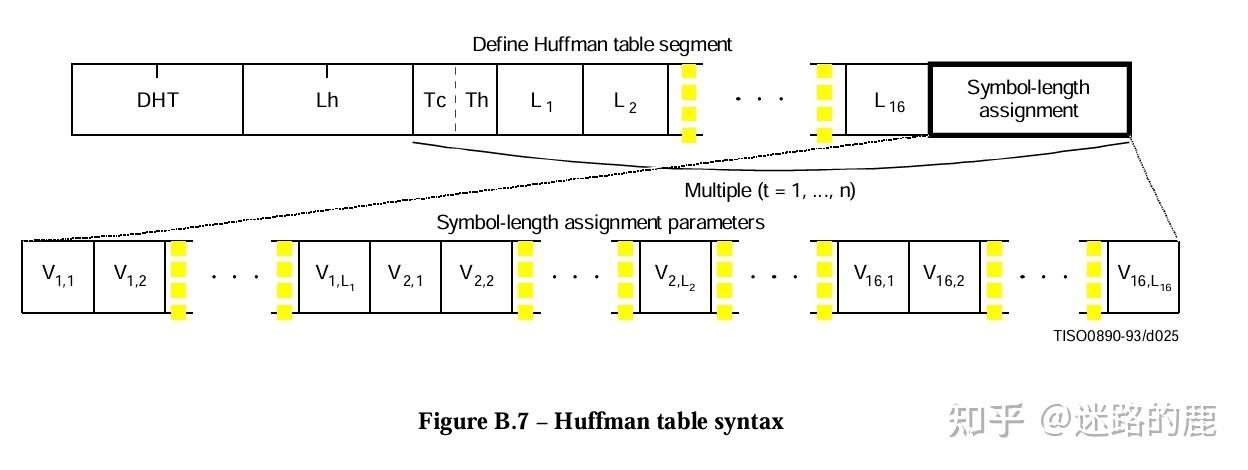
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Lh | 16 | 表示这一个TAG的长度(包括TAG类型的两个字节) |
| Tc | 4 | Table class,0=DC表,1=AC表 |
| Th | 4 | Huffman table destination identifier,表示该哈夫曼表的id |
| Li | 8 | 表示这一长度的编码个数 |
| V i,j | 8 | 表示编码前的原始数据 |
一个DHT中的哈夫曼表个数可以通过长度Lh算出:

其中

除了TAG类型和Lh一个TAG只有一个外,其余的都是每个哈夫曼表都有的。
Th之后是一个长度为16字节的数组,分别对应长度从1bit到16bit的编码个数。
再之后存的是各个编码对应的原始数据(以字节为单位)。JPEG采用的范式哈夫曼编码,可以这些信息推导出数据编码前后的对应关系。
DQT的结构与DHT结构相似,比DHT还稍微简单一些
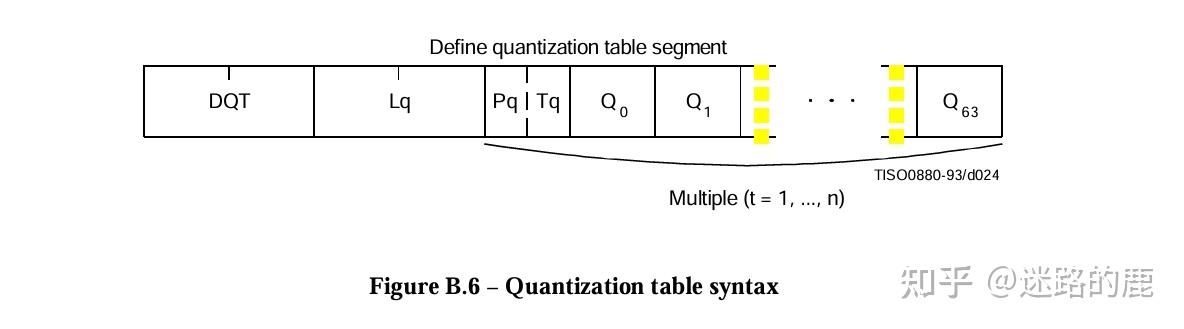
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Lq | 16 | 与Lh意义相同,表示这一TAG的长度 |
| Pq | 4 | 量化表的精度,0=8bit,1=16bit |
| Pq | 4 | 量化表的id |
| Qk | 8 | 量化表中的数据 |
量化表大小固定为8x8,也就是一个表有64个数,DQT长度与量化表个数也有类似的关系:

SOF(Start of Frame) TAG的结构如下:
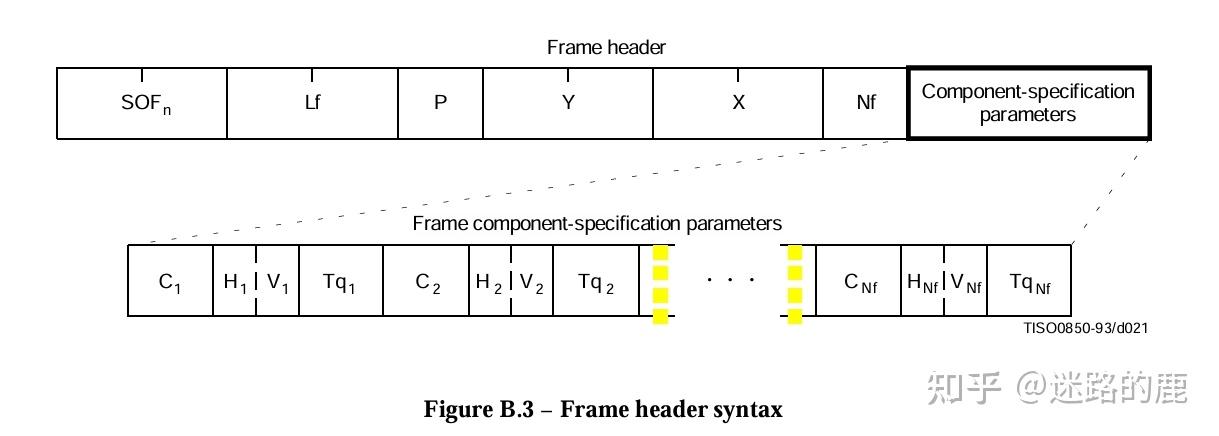
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Lf | 16 | 这一TAG的长度 |
| P | 8 | 采样精度 |
| Y | 16 | 图片的高度 |
| X | 16 | 图片的宽度 |
| Nf | 4 | Component的个数 |
Component的结构如下:
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Ci | 8 | Compoenent的id |
| Hi | 4 | 水平缩放因子 |
| Vi | 4 | 垂直缩放因子 |
| Tqi | 8 | 对应的量化表id |
根据我的理解,这里的Component个数相当于色度分量的个数,比如RGB和YUV都是3,灰度图像则是1.
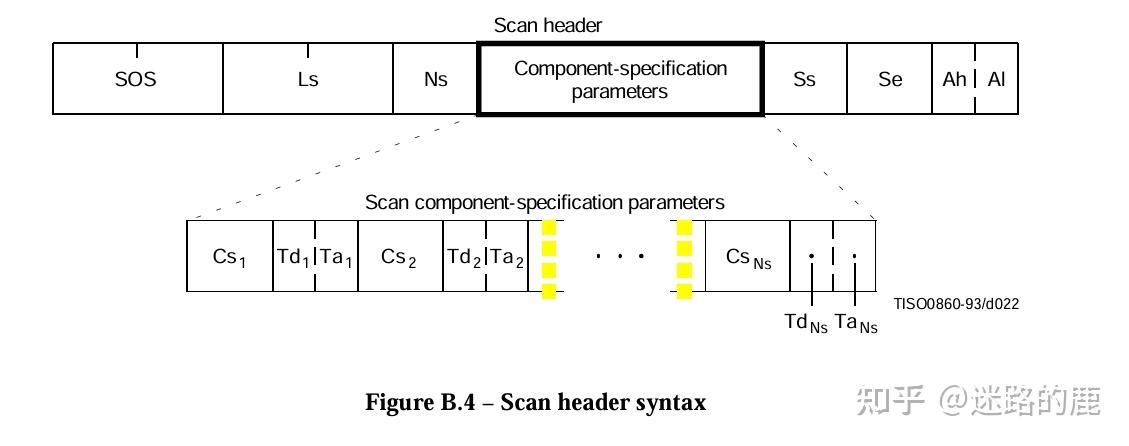
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Ls | 16 | 这一TAG的长度 |
| Ns | 8 | 一个scan内的component数量 |
| Ss | 8 | 没用 |
| Se | 8 | 没用 |
| Ah | 4 | 没用 |
| Al | 4 | 没用 |
Scan中还描述了这一Scan内不同Component中哈夫曼表和量化表的对应关系:
| 名称 | 长度(bit) | 备注 |
|---|---|---|
| Csi | 8 | 通过id选择Component |
| Tdi | 4 | 通过id选择DC哈夫曼表 |
| Tai | 4 | 通过id选择AC哈夫曼表 |
到这里JPEG解码所需要的几个重要TAG的结构就介绍完了,接下来就做好准备工作就可以开始解码了。
JPEG解码系列博客:多媒体-编解码 - 随笔分类 - OnlyTime_唯有时光 - 博客园 (cnblogs.com)
JPEG标准:Microsoft Word - T081E.DOC (w3.org)
一个Rust写的JPEG解码器:MROS/jpeg_tutorial: 跟我寫 JPEG 解碼器 (Write a JPEG decoder with me) (github.com)
我学习过程中写的JPEG图片查看器:Ryan1202/my-tiny-jpeg-viewer: A Tiny Jpeg Viewer (github.com)
下一章:迷路的鹿:JPEG格式研究——(3)霍夫曼解码
因为霍夫曼编码以bit为单位,长度又不确定,读取时无法区分,JPEG采用了范式霍夫曼编码。
JPEG中DC系数和AC系数是分别进行编码将霍夫曼表保存在DQT中。
直接上代码解释可能更直接:
let mut code = 0usize; let mut length = [0; 16]; for i in 0..16 { length[i] = data[offset + i + 1]; for j in 0..length[i] as usize { if code >= (1 << (i + 2)) { return Err(HuffmanErrorType::InvalidCode(data[off + j], code)); } map.insert(Binary::new(code, i + 1), data[off + j]); code += 1; } off += length[i] as usize; code <<= 1; } 首先定义了一个变量code,用于计算对应的编码,根据范式霍夫曼编码的计算方法从0开始。因为霍夫曼编码的长度最大为16bit,所以用了长16字节的数组,保存了不同长度的编码个数
讯享网let mut code = 0usize; let mut length = [0; 16];
然后依次读取不同长度的编码个数
for i in 0..16 { length[i] = data[offset + i + 1]; … } 然后根据编码长度进行循环计算,相同长度的编码每计算出一个就将code+1。这里为了后面解码方便直接用map保存键值对。
Binary是一个保存了值和二进制长度的结构体,用于区分不同长度的二进制串
讯享网for j in 0..length[i] as usize { // 错误处理部分省略 map.insert(Binary::new(code, i + 1), data[off + j]); code += 1; }
然后在编码长度+1时将code左移一位
code <<= 1; 霍夫曼表数量=颜色分量数2,比如RGB和YCbCr都是3个颜色分量,而灰度则是1个颜色分量,颜色分量数以及每一个颜色分量的DC、AC系数解码所需的霍夫曼表编号都保存在SOF中。
选择出需要的DC、AC系数的霍夫曼表后,就可以开始解码了
JPEG中将图像按8x8大小进行分块,所以都是以64个数为一组进行解码的,其中第一个数是DC系数,其余的63个则是AC系数
DC系数需要首先读取一个经过霍夫曼编码的数据,这个数表示需要读取的bit长度。再以这一长度读取一个二进制串(未经过霍夫曼编码),如果长度为0则表示这里的数据就是0。
这一个二进制串的最高位是符号位,为1表示正数,为0表示负数,如果只有1位那就是只有符号位。然后要对符号位之外表示的数按位取反,按符号位得出正负得到DPCM编码。
DPCM编码实际上也很简单,就是加上上一个DC系数就好了(如果是第一个DC系数则不用加或者加0)
代码如下:
讯享网let codeval = dc.huff.decode(bs)?; let len = codeval as usize; if len == 0 { code[0] = last_dc; } else if len == 1 { code[0] = last_dc + bs.read(len)? as isize 2 - 1; // 0 -> -1, 1 -> 1 } else { let sign = bs.read(1)?; let num = sign << (len - 1) | bs.read(len - 1)?; let result; if sign == 0 { result = -(((!num) & ((1 << len) - 1)) as isize); // Rust中按位取反是!有点不适应 } else { result = num as isize; } code[0] = result + last_dc; }
先用霍夫曼解码出一个数,这个数的高4位表示0的个数,而低4位后面的数据的bit长度。其中有两种特殊情况:全为0则是EOB(End Of Block),直接结束AC系数解码,剩余的部分用0填充;高4位为1,低4为0则表示有连续16个0.
后面读取出的数据和DC系数解码的方式一样,先是1位符号位,后面跟着剩余位的数据。
代码如下:
let mut i = 1; while i < 64 { let codeval = ac.huff.decode(bs)?; let zero = codeval >> 4; let len = (codeval & 0x0f) as usize; if len == 0 { if codeval == 0xf0 { // 连续16个0 i += 16; continue; } else { // End Of Block,直接结束 break; } } else if len == 1 { i += zero as usize; code[i] = bs.read(len)? as isize * 2 - 1; // 0 -> -1, 1 -> 1 } else { let sign = bs.read(1)?; let num = sign << (len - 1) | bs.read(len - 1)?; let result; if sign == 0 { result = -(((!num) & ((1 << len) - 1)) as isize); } else { result = num as isize; } i += zero as usize; code[i] = result; } i += 1; } 博客园博客:JPEG解码——(4)霍夫曼解码 - OnlyTime_唯有时光 - 博客园 (cnblogs.com)
JPEG标准:Microsoft Word - T081E.DOC (w3.org)
一个Rust写的JPEG解码器:MROS/jpeg_tutorial: 跟我寫 JPEG 解碼器 (Write a JPEG decoder with me) (github.com)
我学习过程中写的JPEG图片查看器:Ryan1202/my-tiny-jpeg-viewer: A Tiny Jpeg Viewer (github.com)

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/196264.html