2025年分层图是什么意思？（分层图是什么意思）

科技前沿 • 2025-05-31 23:33 • 阅读 33

大家好，我是讯享网，很高兴认识大家。

前置芝士：最短路算法

所谓分层图，即把一整个完整的图，分为若干层，每层对应着原图中的某种状态。

分层图每一层大致有如下特点：

而分层图的边通常有两种情况：

注意： 由于有很多层，分层图的数据范围通常和状压一样，有很明显的特征，如果数据很大那么分层图可能不适用。

Revamping Trails G

约翰一共有个牧场.由条布满尘埃的小径连接。小径可以双向通行。每天早上约翰从牧场出发到牧场去给奶牛检查身体。

通过每条小径都需要消耗一定的时间。约翰打算升级其中条小径，使之成为高速公路。在高速公路上的通行几乎是瞬间完成的，所以高速公路的通行时间为。

请帮助约翰决定对哪些小径进行升级，使他每天从号牧场到第号牧场所花的时间最短。

如果直接枚举所有可能的高速公路情况，需要枚举时间复杂度是，绝对不行。

可以发现，如果按升级的高速公路数量为依据，对原图所有状态进行划分，将其分为：

按照连边的思想，应该这么连：

一条边，其中在同一层，那么不做改变，连接一条到，权重为的边，表示布满尘埃的小径；
一条边，其中在层，在层（规定不能一次性修建两条或删除高速公路），那么做改变，连接一条到，权重为的边，的具体值在此题中应为，相当于原本要花费，但是现在免费了，同时状态改变，表示高速公路。

而最后的答案即为每一层，也就是修建任意条高速公路中号点的最短路中的最小值

对样例进行建图：

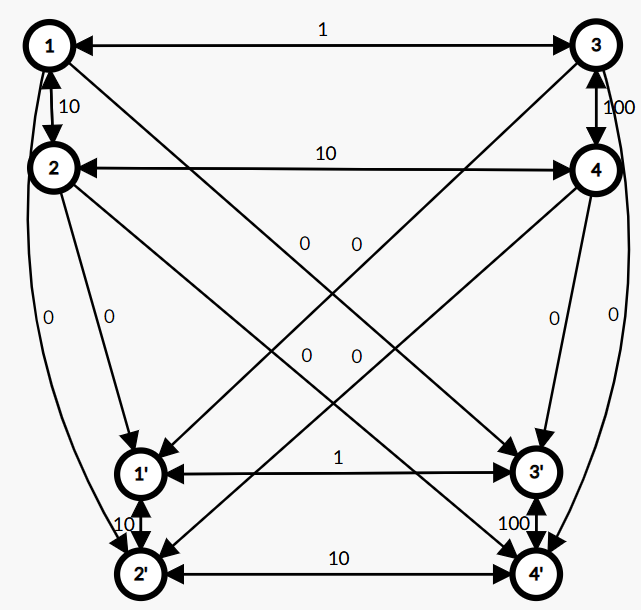
由于所以只有两层，分别对应和。

如果不修建高速公路，路径是，答案是；

如果修建一条高速公路，路径是，答案是

正确答案是：

Code

讯享网

孤岛营救

前置芝士：

一个网格图，其中格子之间有墙或是门，门需要拿到对应的钥匙才可以开启，钥匙分布在网格图之中，问从走到的最短距离。

可以发现，这题的钥匙种类，因此可以以这个为依据分层。

同时发现一个性质，如果当前格子有钥匙那么就一定会拿，这样可能不赚，但是绝对不亏，所以如果当前格子有钥匙，就向下一层连一条边权为的边，再加上原本的图，分层图就建好了。

由于边权只有我们可以采用实现算法。

我的代码采用逻辑建边。

Code

讯享网

[TJOI2019]大中锋的游乐场

这是我的题解，如有错误，恳请各位大佬指出：[TJOI2019]大中锋的游乐场题解