广度优先搜索树是最小生成树嘛（广度优先搜索的生成树）

科技前沿 • 2025-06-02 11:29 • 阅读 42

大家好，我是讯享网，很高兴认识大家。

　　G=(V,E)

　　G代表图

　　V代表|V|为结点数

　　E代表|E|为边的条数

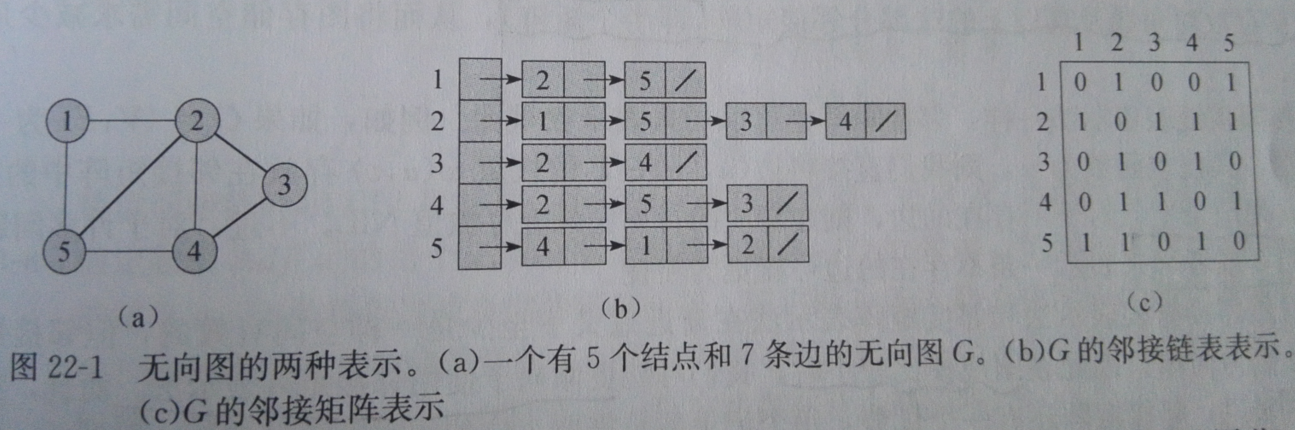
　　图的常规标准表示方式有两种，一种是邻接链表、一种是邻接矩阵。

　　在稀疏图中多用链表，稠密图中多用矩阵。（稀疏与稠密看的是|E|与|V|的2次方的比较，|E|远远小于|V|的2次方为稀疏图）

　　邻接链表的一大缺点是无法快速判断一条边是否是图中的，唯一的办法是搜索结点找边。

　　图规模比较小时，更倾向于使用邻接矩阵表示法。

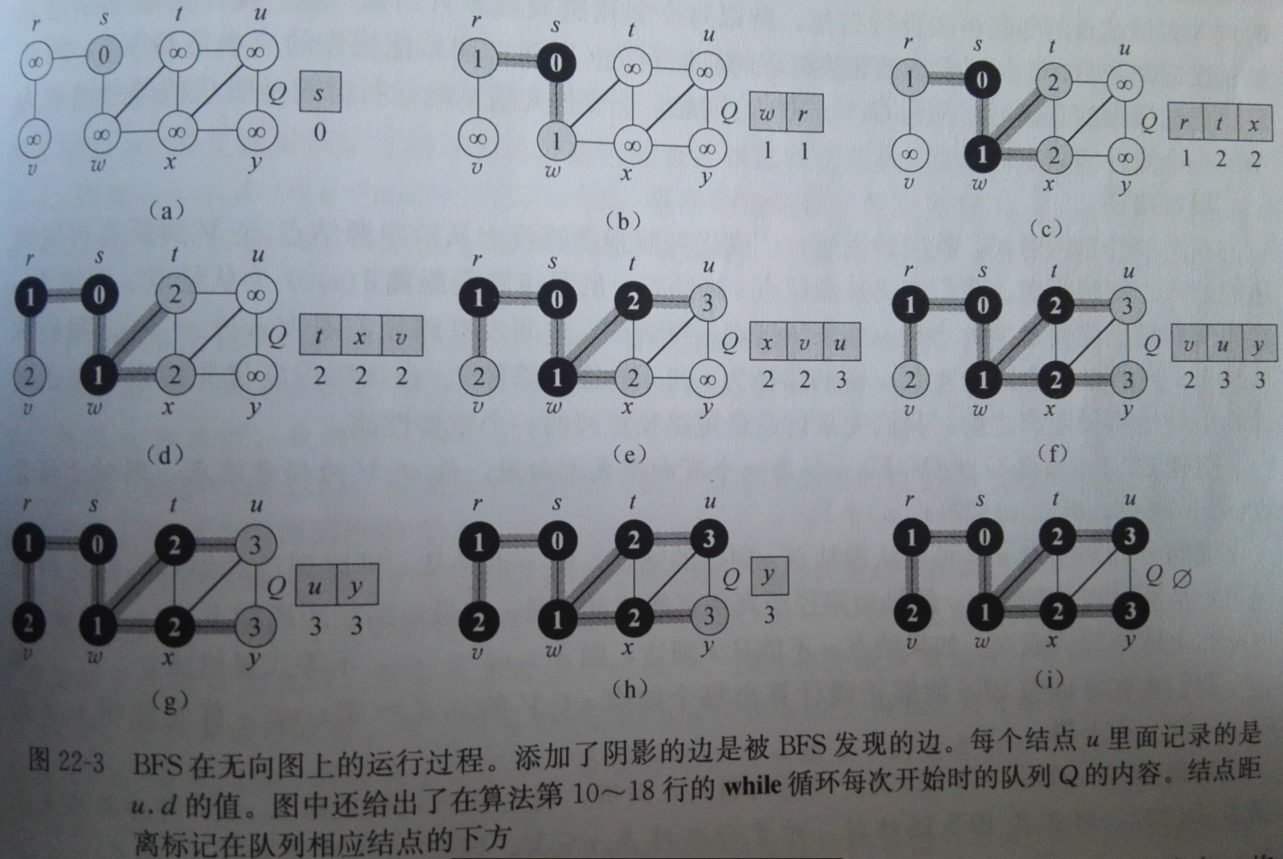
　　Prim的最小生成树算法和Dijkstra的单源最短路径算法都用了广度优先搜索。

　　无向图中的最小权重树为最小生成树

　　定义：在连通无向图G=(V,E)中找到一个无环子集T属于E，既能够将所有的结点（针脚）连接起来，又具有最小的权重。由于T是无环的，并且连通所有结点，因此，T必然是一棵树。我们称之为最小生成树。

　　这两个算法都是最小生成树算法

　　每次找最小的边，看是否在同一个树里（边（u，v）中u和v都在树里则为不安全）

　　用的贪心策略

　　下面为伪代码和解释

　　从一个点开始贪心其中最小的权边加入树中

　　下面为伪代码

　　定义：给定一个图G=（V,E），我们希望找到从给定源结点s∈V到每个结点v∈V的最短路径。

　　几个变体问题：

　　　　1）单目的地最短路径问题：每个结点v到给定目的地点的最短路径

　　　　2）单结点对最短路径问题：结点u到结点v的最短路径

　　　　3）所有结点对最短路径问题：对于每个结点u和v，找到其最短路径

　　两个结点之间的一条最短路径包含着其他的最短路径（最短路径的子路径也是最短路径）。

　　用前驱子图的表示方法，具体形式为每个结点开辟一个空间存储它的上一结点。（其实另开辟一个数组也是可以的）

　　松弛技术：对于每个结点v来说，我们维持一个属性v.d，用来记录从源结点s到结点v的最短路径权重的上界。我们称v.d为s到v的最短路径估计。

　　松弛过程：v结点本身有一个最短估计值为v.d，又找到一条到v的路径把权值跟v.d进行比较，如果后者小，则更新v.d和v.π。

　　以下是伪代码

　　注意：此算法可处理边权值为负值的情况，此算法可判断出负值成环的存在。

　　以下为伪代码

　　根据结点的拓扑排序次序来对带权重的有向无环图G=（V，E）进行边的松弛。

　　注意：1.如果源结点s不是拓扑排序后的第一个结点，直到找到源结点s前的所有结点可以无视。

　　　　　2.边权非负

　　以下是伪代码

　　解决带权重的有向图上单源最短路径问题

　　注意：1.边权非负

　　　　　2.Dijkstra算法比Bellman-Ford算法运行速度快。

　　算法核心思想：重复从结点集V-S中选择最短路径估计最小的结点u，加入集合S，对从u出发的边进行松弛。（V为全部结点集合，S为已使用结点集合）

　　以下是伪代码