泊松分布的基本描述:
泊松分布在对一个时间或空间间隔内事件发生的次数的建模是非常常用的。
泊松分布的例子:
①1年内落到地球上直径大于1米的流星的
②在晚上10点到11点内到达急诊室的病人的数量。
泊松分布建模必须满足的假设:
①变量k表示的是在一个区间内事件发生的次数,且k能够从0到n取值。
②事件的发生时相互独立的。
③事件发生率的常数,也就是说在相同的长度的间隔内,事件平均发生的次数是一样的。
④某一个瞬间只能发生一个事件。
⑤事件发生的概率与区间是成比例的。
⑥泊松分布能够由一个二项分布给出。
泊松分布中事件概率的计算:
在一个区间内事件可以发生0次,1次,2次,...,那么在这个区间内,事件发生的平均次数我们称之为λ(lambda)。lambda又叫做事件率,或者是率参数。通过引入lambda,我们可以计算出一个区间内事件发生k次的概率,由以下公式给出。

这里λ表示在每个区间内时间发生的平均次数,e是自然常数,k能够从0到n取值。这个方程就是泊松分布的概率质量函数(PMF)。由于在计算机中计算指数项以及阶乘项会很容易发生溢出的情况,而且四舍五入可能会产生误差,因此我们可以等价地改变方程的表示来满足计算机的计算特性。公式如下。

泊松分布的一些属性:
①泊松分布的期望值和方差都等于lambda。
②满足泊松分布的多个相互独立的随机变量之和仍是满足泊松分布的,lambda为所有泊松分布变量的lambda之和。
泊松分布的属性图:
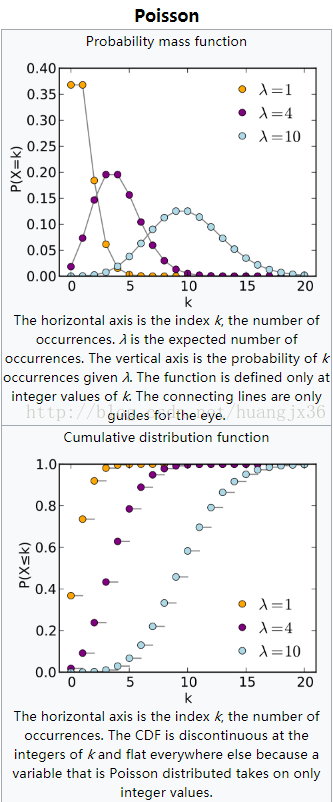
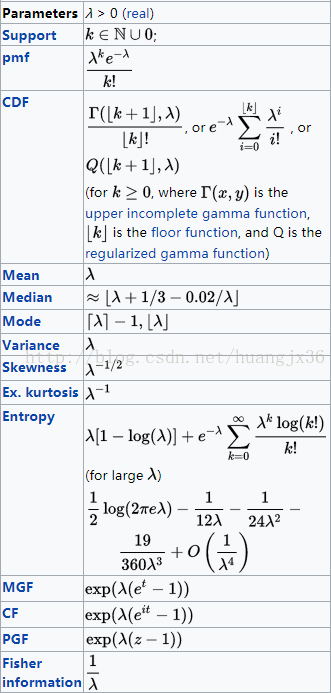
参考资料:
泊松分布-维基百科 https://en.wikipedia.org/wiki/Poisson_distribution


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/136066.html