2025年单摆控制教程

大家好，我是讯享网，很高兴认识大家。

1. 单摆模型

$\ddot{\theta} = -asin(\theta)-b\dot{\theta}+cT$
讯享网

为使得单摆在 $\theta = \delta$ 处保持平衡，力矩必须有一个稳态分量 $T_{ss}$ 满足

$0 = -asin(\delta)+cT_{ss}$

选择状态变量为 $x_1 = \theta-\delta, x_2 = \dot{\theta}$ , 控制变量为 $u = T- T_{ss}$ ,则状态方程变为

$\dot{x}_1=x_2$

$\dot{x}_2=-a[sin(x_1+\delta)-sin(\delta)]-bx_2+cu$

2. 线性化控制

将系统在原点线性化得：

$A= \begin{bmatrix} 0 & 1 \\ -acos(x_1+\delta) & -b \end{bmatrix} =\begin{bmatrix} 0 & 1 \\ -acos(\delta) & -b \end{bmatrix} B= \begin{bmatrix} 0 \\ c \end{bmatrix}$

取 K = [k_1,k_2] ，容易验证当

$k_1>-\frac{acos{\delta}}{c},k_2>\frac{b}{c}$

时，A-BK是赫尔维茨矩阵，力矩为

$T=\frac{asin(\delta)}{c}-Kx=\frac{asin(\delta)}{c}-k_1(\theta-\delta)-k_2\dot{\theta}$

3. matlab仿真代码

%=========== 单摆控制-状态反馈 ===========% clear all;clc;close all; %% 参数设置 g = 9.8; % 重力加速度 l = 1; % 摆长 k = 0.5; % 摩擦系数 m = 1; % 摆球质量 a = g/l; b = k/m; c = 1/(m*l^2); theta(1) = 0; delta = -pi/5; dtheta(1) = 0.2; interval = 0.05; t = 0:interval:40; k1 = -a*cos(delta)+5; k2 = -b/c + 5; A = [0 1; -a*cos(delta) -b]; B = [0;c]; K = [k1 k2]; eig(A - B*K) %% 状态变化 for i = 2:1:length(t) T = a*sin(delta)/c - k1*(theta(i-1)-delta) - k2*dtheta(i-1); % T = 0; ddtheta = -a*sin(theta(i-1)) - b*dtheta(i-1) +c*T; dtheta(i) = dtheta(i-1) + ddtheta*interval; theta(i) = theta(i-1) + dtheta(i)*interval; end figure plot(t,theta,'r') figure %绘制横梁 colordef black plot([-0.2;0.2],[0;0],'-y','LineWidth',20); x0=l*sin(theta(1));% 初始 x 坐标 y0=-l*cos(theta(1));% 初始 y 坐标 axis([-0.75,0.75,-1.25,1.25]); axis off %创建摆锤 %擦除模式为 xor % head=line(x0,y0,'color','r','linestyle','.',... % 'erasemode','xor','markersize',40); hold on %创建摆杆 body=line([0;x0],[-0.05;y0],'color','g','linestyle','-','erasemode','xor','LineWidth',2); head = []; for i = 2:1:length(t) x=l*sin(theta(i)); y=-l*cos(theta(i)); % set(head,'xdata',x,'ydata',y);% 改变擦除对象的坐标数据 set(body,'xdata',[0;x],'ydata',[-0.05;y]); delete(head); head = plot(x,y,'m.','MarkerSize',40); drawnow;% 刷新屏幕 pause(0.1) F = getframe(gcf); I = frame2im(F); [I,map] = rgb2ind(I,256); if (i == 2) imwrite(I,map,'single.gif','gif','Loopcount',inf,'Delaytime',0.2); else imwrite(I,map,'single.gif','gif','WriteMode','append','DelayTime',0.2); end end

讯享网

4. 控制效果

5. 积分控制

积分控制中，不用寻找计算为保持平衡位置所需要的稳态力矩。此时的反馈控制率为：

$u= -k_1(\theta-\delta)-k2\dot{\theta}-k_3\sigma$

$\dot{\sigma}=\theta-\delta$

加入积分控制后，即不需要再寻找平衡力矩就可以实现稳态控制

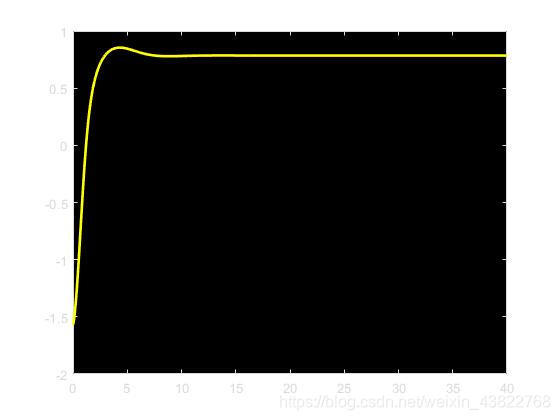
6. 仿真结果

讯享网%=========== 单摆控制-线性化状态反馈 ===========% clear all;clc;close all; %% 参数设置 g = 9.8; % 重力加速度 l = 1; % 摆长 k = 0.5; % 摩擦系数 m = 1; % 摆球质量 a = g/l; b = k/m; c = 1/(m*l^2); theta(1) = -pi/2; delta = pi/4; dtheta(1) = 0.2; interval = 0.05; t = 0:interval:40; k1 = -a*cos(delta)+5; k2 = -b/c + 5; A = [0 1; -a*cos(delta) -b]; B = [0;c]; K = [k1 k2]; k3 = 3; eig(A - B*K) alpha(1) = 0; %% 状态变化 for i = 2:1:length(t) % T = a*sin(delta)/c - k1*(theta(i-1)-delta) - k2*dtheta(i-1); % T = 0; dalpha = theta(i-1) - delta; alpha(i) = alpha(i-1) + dalpha*interval; T = - k1*(theta(i-1)-delta) - k2*dtheta(i-1) -k3*alpha(i); ddtheta = -a*sin(theta(i-1)) - b*dtheta(i-1) +c*T; dtheta(i) = dtheta(i-1) + ddtheta*interval; theta(i) = theta(i-1) + dtheta(i)*interval; end figure plot(t,theta,'y','LineWidth',2) figure %绘制横梁 colordef black plot([-0.2;0.2],[0;0],'-y','LineWidth',20); x0=l*sin(theta(1));% 初始 x 坐标 y0=-l*cos(theta(1));% 初始 y 坐标 axis([-1,1,-1.25,1.25]); axis off %创建摆锤 %擦除模式为 xor % head=line(x0,y0,'color','r','linestyle','.',... % 'erasemode','xor','markersize',40); hold on %创建摆杆 body=line([0;x0],[-0.05;y0],'color','g','linestyle','-','erasemode','xor','LineWidth',2); head = []; for i = 2:1:length(t) x=l*sin(theta(i)); y=-l*cos(theta(i)); % set(head,'xdata',x,'ydata',y);% 改变擦除对象的坐标数据 set(body,'xdata',[0;x],'ydata',[-0.05;y]); delete(head); head = plot(x,y,'m.','MarkerSize',40); drawnow;% 刷新屏幕 pause(0.1) % F = getframe(gcf); % I = frame2im(F); % [I,map] = rgb2ind(I,256); % if (i == 2) % imwrite(I,map,'single.gif','gif','Loopcount',inf,'Delaytime',0.2); % else % imwrite(I,map,'single.gif','gif','WriteMode','append','DelayTime',0.2); % end end