原文转载自:http://blog.csdn.net/b2b160/article/details/
遗传算法的手工模拟计算示例
为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各
个主要执行步骤。
例:求下述二元函数的最大值:
(1) 个体编码
遗传算法的运算对象是表示个体的符号串,所以必须把变量 x1, x2 编码为一种
符号串。本题中,用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数,所以分别用3位无符号二进制整数来表示,将它
们连接在一起所组成的6位无符号二进制数就形成了个体的基因型,表示一个可
行解。
例如,基因型 X= 所对应的表现型是:x=[ 5,6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。
(2) 初始群体的产生
遗传算法是对群体进行的进化操作,需要给其淮备一些表示起始搜索点的初始
群体数据。
本例中,群体规模的大小取为4,即群体由4个个体组成,每个个体可通过随机
方法产生。
如:011101,,011100,
(3) 适应度汁算
遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传
机会的大小。
本例中,目标函数总取非负值,并且是以求函数最大值为优化目标,故可直接
利用目标函数值作为个体的适应度。
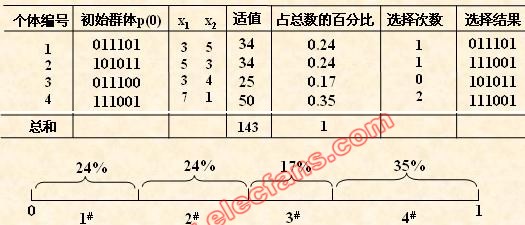
(4) 选择运算
选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代
群体中。
本例中,我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中
的数量。其具体操作过程是:
• 先计算出群体中所有个体的适应度的总和 fi ( i=1.2,…,M );
• 其次计算出每个个体的相对适应度的大小 fi / fi ,它即为每个个体被遗传
到下一代群体中的概率,
• 每个概率值组成一个区域,全部概率值之和为1;
• 最后再产生一个0到1之间的随机数,依据该随机数出现在上述哪一个概率区
域内来确定各个个体被选中的次数。
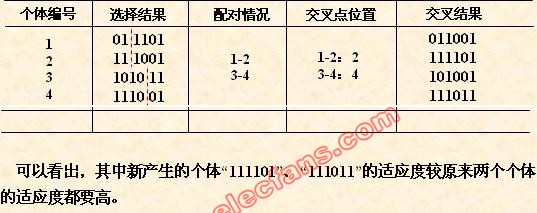
(5) 交叉运算
交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某
两个个体之间的部分染色体。
本例采用单点交叉的方法,其具体操作过程是:
• 先对群体进行随机配对;
• 其次随机设置交叉点位置;
• 最后再相互交换配对染色体之间的部分基因。
(6) 变异运算
变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进
行改变,它也是产生新个体的一种操作方法。
本例中,我们采用基本位变异的方法来进行变异运算,其具体操作过程是:
• 首先确定出各个个体的基因变异位置,下表所示为随机产生的变异点位置,
其中的数字表示变异点设置在该基因座处;
• 然后依照某一概率将变异点的原有基因值取反。
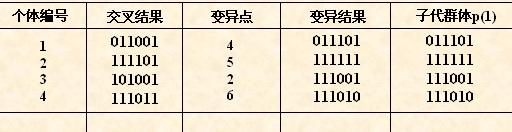
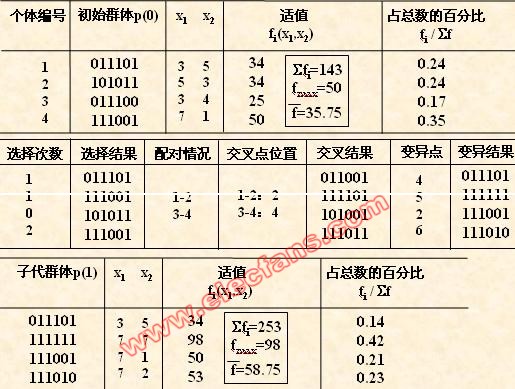
对群体P(t)进行一轮选择、交叉、变异运算之后可得到新一代的群体p(t+1)。
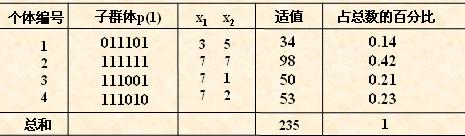
从上表中可以看出,群体经过一代进化之后,其适应度的最大值、平均值都得
到了明显的改进。事实上,这里已经找到了**个体“”。
[注意]
需要说明的是,表中有些栏的数据是随机产生的。这里为了更好地说明问题,
我们特意选择了一些较好的数值以便能够得到较好的结果,而在实际运算过程中
有可能需要一定的循环次数才能达到这个最优结果。
//
1、遗传算法,核心是达尔文优胜劣汰适者生存的进化理论的思想。一个种群,通过长时间的繁衍,种群的基因会向着更适应环境的趋势进化,适应性强的个体基因被保留,后代越来越多,适应能力低个体的基因被淘汰,后代越来越少。经过几代的繁衍进化,留下来的少数个体,就是相对能力最强的个体了。
那么在解决一些问题的时候,我们所学习的便是这样的思想。比如先随机创造很多很多的解,然后找一个靠谱的评价体系,去筛选适应性高的解,再用这些适应性高的解衍生出更好的解,然后再筛选,再衍生。反复迭代一定次数,可以得到近似最优解。
2、首先,我们先看看一个经典组合问题:“背包问题”
“背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。”
这个问题的衍生简化问题 “0-1背包问题” 增加了限制条件:每件物品只有一件,可以选择放或者不放,更适合我们来举例这样的问题如果数量少,当然最好选择穷举法
比如一共3件商品,用0表示不取,1表示取,那么就一共有
000 001 010
011 100 101
110 111
这样8种方案,然后让计算机去累加和,与 重量上限 比较,留下来的解里取最大即可。
但如果商品数有300,3000,甚至3w种呢,计算量太大穷举法可能就不适用了,这时如果遗传算法使用得当,就能在较短的时间内帮我们找到近似的最优解,我们继续往下看:
新的问题是12件商品的0-1背包问题
我们先让计算机随机产生1000个12位的二进制数。把总重量超过背包上限的解筛掉,剩下的两两一对随机交换“基因片段”产生下一代
交换前:
0000 1100 1101
0011 0101 0101
交换后:
0000 0101 1101
0011 1100 0101
再筛选,再交配,如此反复几代,留下的“基因型“差不多就是最好的了,如此这般与生物进化规律是一样的。
同时,在生物繁殖过程中,新产生的基因是有一定几率突变的,这是很多优良性状的重要来源,遗传算法中可也不能忽略它
比如:
变异前:
000101100101
变异后:
000101110101
三个基本操作:选择,交叉,变异
一.适度函数
适度函数其实就是指解的筛选标准,比如上文所说的把所有超过上限重量的解筛选掉,但是不是有更好的筛选标准呢?这将直接影响最后结果的 接近程度 以及 求解所耗费的时间 ,所以设置一个好的适度函数很重要
二.选择
在遗传算法中 选择 也是个概率问题,在解的范围中 适应度 更高的基因型有 更高的概率 被选择到。所以,在选择一些解来产生下一代时,一种常用的选择策略是 “比例选择” ,也就是个体被选中的概率与其适应度函数值成正比。假设群体的个体总数是M,那么那么一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) )。常用的选择方法――轮盘赌(Roulette Wheel Selection)选择法。
三.交叉
在均等概率下基因位点的交叉,衍生出新的基因型。上述例子中是通过交换两个基因型的部分”基因”,来构造两个子代的基因型。
四.变异
在衍生子代的过程中,新产生的解中的“基因型”会以一定的概率出错,称为变异。变异发生的概率设置为Pm,记住该概率是很小的一个值。因为变异是小概率事件!
五.基本遗传算法优化
为了防止进化过程中产生的最优解被变异和交叉所破坏。《遗传算法原理及应用》介绍的最优保存策略是:即当前种群中适 应度最高 的个体不参与交叉运算和变异运算,而是用它来替换掉本代群体中经过交叉、变异等遗传操作后所产生的适应度最低的个体。
遗传算法的优点:
1、 与问题领域无关且快速随机的全局搜索能力。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,复盖面大,利于全局择优。
2、 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较,鲁棒性高!
3、 搜索使用评价函数启发,过程简单。
4、使用概率机制进行迭代,具有随机性。遗传算法中的选择、交叉和变异都是随机操作,而不是确定的精确规则。这说明遗传算法是采用随机方法进行最优解搜索,选择体现了向最优解迫近,交叉体现了最优解的产生,变异体现了全局最优解的复盖。

5、具有可扩展性,容易与其他算法结合。遗传算法求解时使用特定问题的信息极少,仅仅使用适应值这一信息进行搜索,并不需要问题导数等与问题直接相关的信息。遗传算法只需适应值和串编码等通用信息,故几乎可处理任何问题,容易形成通用算法程序。
6、具有极强的容错能力。遗传算法的初始串集本身就带有大量与最优解甚远的信息;通过选择、交叉、变异操作能迅速排除与最优解相差极大的串;这是一个强烈的滤波过程;并且是一个并行滤波机制。故而,遗传算法有很高的容错能力。
遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。
遗传算法的缺点:
1、遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码
2、三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验
3、没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间
4、算法对初始种群的选择有一定的依赖性(下图所示),能够结合一些启发算法进行改进
5、算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
同时,遗传算法的 局部搜索能力较差 ,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生过早收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。下面举例来说明遗传算法用以求函数最大值
函数为y = -x2+ 5的最大值,-32<=x<=31
一、编码以及初始种群的产生
编码采用二进制编码,初始种群采用矩阵的形式,每一行表示一个染色体,每一个染色体由若干个基因位组成。关于染色体的长度(即基因位的个数)可根据具体情况而定。比如说根据要求极值的函数的情况,本文-32<=X<=31,该范围内的整数有64个,所以可以取染色体长度为6,(26=64)。综上所述,取染色体长度为6,前5个二进制构成该染色体的值(十进制),第6个表示该染色体的适应度值。若是所取得染色体长度越长,表示解空间搜索范围越大,对应的是待搜索的X范围越大。关于如何将二进制转换为十进制,文后的C代码中函数x即为转换函数。
初始种群结构如下图所示:
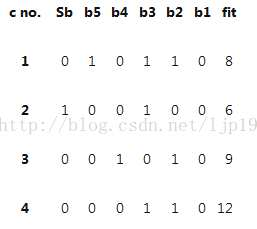
该初始种群共有4个染色体,第1列表示各个染色体的编号,第2列表示该染色体值的正负号,0表示正,1表示负。第3列到第7列为二进制编码,第8列表示各个染色体的适应度值。第2列到第7列的0-1值都是随机产生的。
二、适应度函数
一般情况下,染色体(也叫个体,或一个解)的适应度函数为目标函数的线性组合。本文直接以目标函数作为适应度函数。即每个染色体的适应度值就是它的目标函数值,f(x)=-x^2+ 5。
三、选择算子
初始种群产生后,要从种群中选出若干个体进行交叉、变异,那么如何选择这些个体呢?选择方法就叫做选择算子。一般有轮盘赌选择法、锦标赛选择法、排序法等。本文采用排序法来选择,即每次选择都选出适应度最高的两个个体。那么执行一次选择操作后,得到的新种群的一部分为下图所示:

四、交叉算子
那么接下来就要对新种群中选出的两个个体进行交叉操作,一般的交叉方法有单点交叉、两点交叉、多点交叉、均匀交叉、融合交叉。方法不同,效果不同。本文采用最简单的单点交叉。交叉点随机产生。但是交叉操作要在一定的概率下进行,这个概率称为交叉率,一般设置为0.5到0.95之间。通过交叉操作,衍生出子代,以补充被淘汰掉的个体。交叉后产生的新个体组成的新种群如下:

黑体字表示子代染色体继承父代个体的基因。
五、变异
变异就是对染色体的基因进行变异,使其改变原来的结构(适应值也就改变),达到突变进化的目的。变异操作也要遵从一定的概率来进行,一般设置为0到0.5之间,即以小概率进行基因突变。这符合自然规律。本文的变异方法直接采取基因位反转变异法,即0变为1,1变为0。要进行变异的基因位的选取也是随机的。
六、终止规则
遗传算法是要一代一代更替的,那么什么时候停止迭代呢?这个规则就叫终止规则。一般常用的终止规则有:若干代后终止,得到的解达到一定目标后终止,计算时间达到一定限度后终止等方法。本文采用迭代数来限制。
代码如下所示:
[cpp] view plain copy

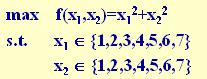
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/46755.html