一、图
图G=（V，E）是由其顶点集V和边集E定义的。在无向图中，边集是一组无序的顶点对。 图（也称为“网络”）通常用于建模事物之间的连接或关系，其中“事物”是顶点。
常见的“自然”图形示例有：
- 友谊图：人是顶点，边存在于朋友对之间（假设关系是对称的）；
- 网络图：设备、路由器和计算机是顶点，边缘存在于连接的对之间；
- 电路图：电子元件是顶点，边缘存在于由电线连接的对之间；
- 蛋白质-蛋白质相互作用图：蛋白质是顶点。边表示相互作用。
二、图的矩阵
2.1 Matrix as a Spreadsheet
我们通常为图的顶点集写V，让n表示顶点的数量。有时我们需要对顶点进行排序并为其分配编号。在这种情况下，它们通常是{1，…，n}。例如，如果我们希望绘制一个矩阵作为表，那么我们需要确定哪个顶点对应于哪个行和列。与图G关联的最自然的矩阵是其邻接矩阵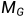
讯享网:
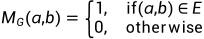
2.2 Matrix as an Operator
2.1.1 概率转移矩阵
与图G相关的最自然的算子可能是其扩散算子。该运算符描述了图顶点之间的物质扩散。想象一个过程，其中每个顶点都可以包含一定量的物质（例如气体）。在每个时间步，顶点处的填充物将均匀分布到其邻居。顶点处的任何东西都不会保留在顶点处，但可以从其他顶点进入。为了构造扩散矩阵，假设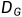
是对角矩阵，其中
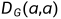是顶点a的度数。我们通常将
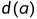写为顶点a的度。
概率转移矩阵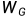
的定义为：
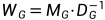
当图是规则的，即每个顶点都具有相同的度数时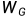，只是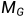的重新缩放。
有时考虑慵懒随机游走更方便。它通常被定义为以一半的概率保持在原地，以一半的几率游走到相邻接点。即：
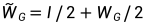
2.2 拉普拉斯矩阵
与图相关联的最自然的二次形式根据其拉普拉斯矩阵来定义，
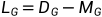
给定顶点上的函数
，其中边（a，b）具有权重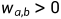
的加权图的拉普拉斯二次型为:
此形式表示函数x的平滑度。如果函数x不在任何边上跳跃明显，那么它就会很小。
三、谱图理论
我们假设向量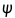
是具有特征值
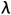的矩阵M的特征向量，如果 
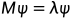,也就是说λ是特征值当且仅当
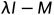是奇异矩阵。
定义3.1【正定/半正定】如果矩阵是对称的并且其所有特征值都是正的，则矩阵是正定的。如果它是对称的，并且它的所有特征值都是非负的，则它是半正定的。
定理3.2【谱定理】如果M是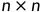
的实对称矩阵，则存在实数
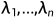和n个相互正交的单位向量
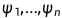，并且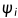
是矩阵M中特征值
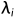的特征向量。
如果矩阵不是对称的，它可能没有n个特征值。 而且，即使它有n个特征值，它们的特征向量也不会是正交的。如果M不是对称的，那么研究它的特征值和特征值可能是错误的。
定理3.4 对于任意图G，图的拉普拉斯矩阵是半正定的。 证明：设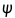是L的特征值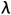的的单位特征向量。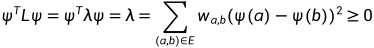 
我们对拉普拉斯算子的特征值从最小到最大进行编号。因此，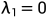
。我们将
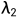到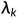
称为低频特征值。
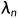是高频特征值。
四、谱图性质
4.1特征向量绘图
低频特征值所对应的特征向量可用于图结构模拟。对于一个 d 维空间的柏拉图立体（即正多面体），将其拉普拉斯矩阵的第 2 至 d+1 个特征值（即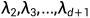
）所对应的特征向量（即
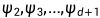）作为对应坐标系的坐标，即可得到该图结构的模拟。下文展示了二维空间的网格图和三维空间的十二面体图上，使用特征向量进行图结构绘制的结果。这一结论的严格证明请见本书第三章。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请联系我们，一经查实，本站将立刻删除。
如需转载请保留出处：https://51itzy.com/kjqy/45059.html