2025年canvas绘图学习：坐标正算

大家好，我是讯享网，很高兴认识大家。

前言

在进行canvas绘图的过程中我遇到了一个问题：我想将圆心与圆的边线上的某个点进行连线，我需要基于圆心坐标、圆半径和连线的角度去计算圆边点的坐标，这实际就是测量学中的坐标正算。

1.坐标正算介绍

坐标正算的概念如下:

根据直线起点的坐标、直线的水平距离及其坐标方位角来计算直线终点的坐标，称为坐标正算。

坐标正算的计算公式如下：

讯享网

2.坐标正算的原理

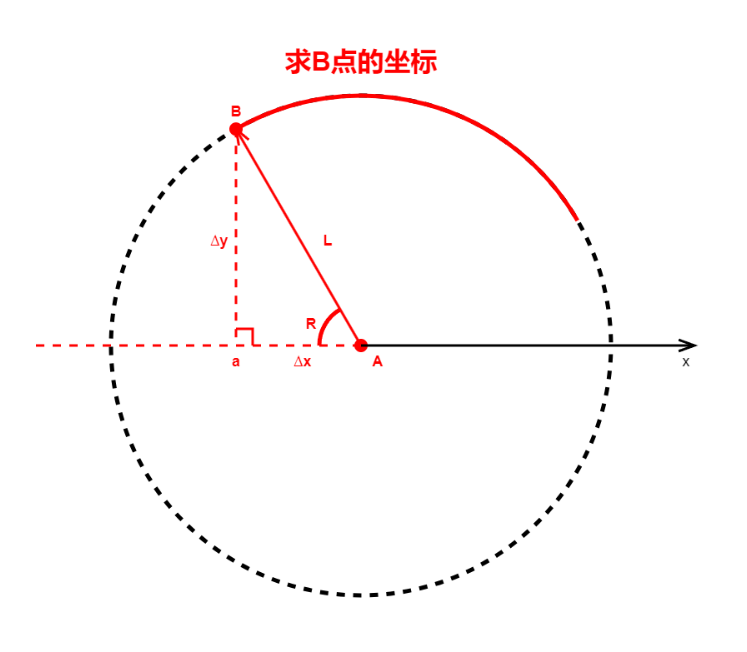
在上图中，已知A点的坐标，要求B点的坐标。可以看出用A点的坐标减去∆x、∆y这两个值就可以算出B点的坐标；而∆x、∆y这两个值都可以用三角函数sin(R)和cos(R)算出；R是直线AB的象限角，可以通过方位角αAB计算出象限角R。

因此坐标正算的步骤如下：

第一步，根据方位角计算出象限角

第二步，使用三角函数计算出坐标增量

第三步，用起始点坐标加减坐标增量得到未知的结束点坐标

3.坐标方位角与象限角

我们先了解一下测量学中坐标方位角和象限角的概念：

坐标方位角是平面直角坐标系中某一直线与坐标主轴（X轴正北向）之间的夹角，从主轴起算，顺时针方向旋转。

以基本方向的北端或南段算起，顺时针或逆时针方向量至直线的水平角，称为象限角。

但是注意canvas坐标系与测量学的平面直角坐标系是有区别的，

canvas坐标系中向右为x轴正方向，向下为y轴正方向
测量平面直角坐标系中向上为x轴正方向，向右为y轴正方向

因此在canvas当中坐标方位角为从x轴正方向开始顺时针旋转到某一直线的角度；象限角为某一直线沿顺时针或逆时针到x轴的角度。

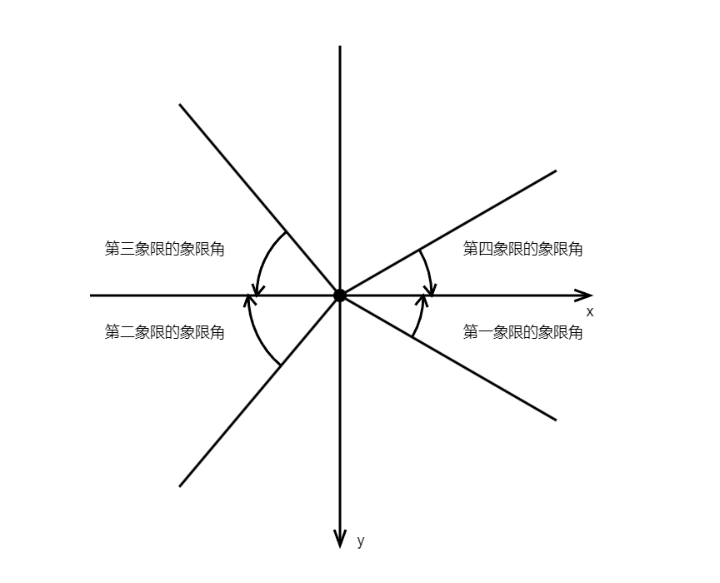
象限角与坐标方位角的转换方式如下：

坐标方位角及其所在的象限	方位角转象限角	象限角转方位角
0° ~ 90° （第一象限）	R = α	α = R
90° ~ 180° （第二象限）	R = 180° - α	α = 180° - R
180° ~ 270° （第三象限）	R = α - 180°	α = R + 180°
270° ~ 360° （第四象限）	R = 360° - α	α = 360° - R

转换成代码就是：

 if ( α >= 0 && α < 90) { R = α } else if (α >= 90 && α < 180) { R = 180 - angle } else if (α >= 180 && α < 270) { R = α - 180 } else { R = 360 - α }

讯享网

4.通过三角函数求坐标增量

坐标增量∆x和∆y可以通过三角函数计算出来，公式如下：

∆x = cos(θ) * L

∆y = sin(θ) * L

公式的推导过程如下：

下图中的三角形ABa是一个直角三角形所以可以使用三角函数。因为sin() = 对边/斜边cos() = 临边/斜边，所以sin(R) = ∆y / L cos(R) = ∆x / L。最后就可以推导出 ∆x = cos(θ) * 300 ∆y = sin(θ) * 300。

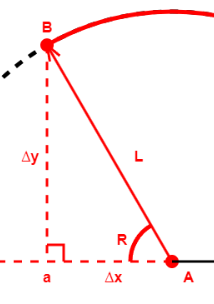
上面的公式可以用如下的代码表示:

讯享网// l是线段的长度 ∆x = Math.cos(R * 180 / Math.PI) * L ∆y = Math.sin(R * 180 / Math.PI) * L

注意：JS的Math.cos()和Math.sin()方法都只接收弧度制角度作为参数，所以普通角度要先乘以 π / 180° 转换为弧度制。

5. 起始点坐标加减坐标增量

在上一节中我们计算出了坐标增量，现在只需要用起始点A的坐标减去坐标增量就可以求出B点的坐标。

由于在上图中B点位于A点的左上方，而在canvas坐标系中越往左x坐标越小，越往上y坐标越小，所以这里要用B点的坐标减坐标增量。

XB = XA - ∆x

YB = YA - ∆y

但是难道所有情况下都是这样计算吗？答案显然是否定的。例如下面的例子中B点就在A点的右上方，因此根据canvas坐标系的规则此时的计算方式就应该是：

XB = XA + ∆x

YB = YA - ∆y

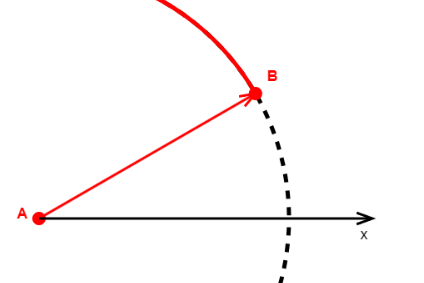
实际上对于坐标增量有如下的两种解释：

（1）坐标增量绝对值说

这种理解的核心观点是：“坐标增量∆x、∆y代表两条线段的长度，所以它们都是正数”。但是与此同时在根据线段的坐标方位角不同，未知点的计算方式也不同，可能是已知点坐标减坐标增量，也可能是已知点坐标加坐标增量。所以计算公式如：

XB = XA ± ∆x

YB = YA ± ∆y

方位角与计算方式的关系如下：

坐标方位角及其所在的象限	未知点的计算方式
0° ~ 90° （第一象限）	XB = XA + ∆x YB = YA + ∆y
90° ~ 180° （第二象限）	XB = XA - ∆x YB = YA + ∆y
180° ~ 270° （第三象限）	XB = XA - ∆x YB = YA - ∆y
270° ~ 360° （第四象限）	XB = XA + ∆x YB = YA - ∆y

（2）坐标增量有符号说

这种解释的核心是“坐标增量是线段两点的坐标差值，因此坐标增量有正有负”。所以计算公式为：

XB = XA + ∆x

YB = YA + ∆y

而坐标增量的符号与坐标方位角有关，它们的关系如下：

坐标方位角及其所在的象限	∆x的符号	∆y的符号
0° ~ 90° （第一象限）	+	+
90° ~ 180° （第二象限）	-	+
180° ~ 270° （第三象限）	-	-
270° ~ 360° （第四象限）	+	-

当然无论基于上面的那种解释，最后实际上都是殊途同归，上面的公式可以转换为如下的代码：

 if (angle >= 0 && angle < 90) { XB = XA + ∆x YB = YA + ∆y } else if (angle >= 90 && angle < 180) { XB = XA - ∆x YB = YA + ∆y } else if (angle >= 180 && angle < 270) { XB = XA - ∆x YB = YA - ∆y } else { XB = XA + ∆x YB = YA - ∆y }

5.封装坐标正算的方法

讯享网/ * * @param {Array} startPoint 起始点坐标 * @param {number} length 线段长度 * @param {number} angle 坐标方位角 */ function calcCoordinate(startPoint, length, angle) { // 第一步:计算象限角 let qAngle // 象限角 if (angle >= 0 && angle < 90) { qAngle = angle } else if (angle >= 90 && angle < 180) { qAngle = 180 - angle } else if (angle >= 180 && angle < 270) { qAngle = angle - 180 } else { qAngle = 360 - angle } // 第二步:计算坐标增量 const _x = Math.cos((qAngle * Math.PI) / 180) * length const _y = Math.sin((qAngle * Math.PI) / 180) * length // 第三步:求未知点坐标 let result const [x, y] = startPoint if (angle >= 0 && angle < 90) { result = [x + _x, y + _y] } else if (angle >= 90 && angle < 180) { result = [x - _x, y + _y] } else if (angle >= 180 && angle < 270) { result = [x - _x, y - _y] } else { result = [x + _x, y - _y] } return result }

参考资料

工程测量（第二版）第六章直线方位角测量
测量员系列二：坐标正反算
方位角与象限角的关系—博客园