集训日记：DAY3

Success is not final, failure is not fatal. It is the courage to continue that counts.
没有最终的成功，也没有致命的失败，最可贵的是继续前进的勇气。
You’re not perfect, but you’re strong. You’re a skeptic, which makes you wise.
虽然你不是完人，可是你很坚强。你抱有怀疑之心，所以你很睿智。
——至暗时刻

开头这两句话送给自己，今天真的可能是OI生涯中的至暗时刻如果明天不会更糟 千万别，在搞心态人没了QAQ。

早8:00到机房，今天考数据结构，发题之前满脑子想的都是线段树毕竟它太强大了 ……
发题之后老规矩先遍历一遍。
第一题……线段树怎么做？区间覆盖……有点麻烦……
第二题……线段树好像没法做……难搞啊！
第三题像个树上问题……好像线段树也没法做……
第四题……二维线段树？（此时过去10min）
如你所见考试前10分钟我想的全是线段树……
在断定线段树已死之后，我开始想其他思路。
观察了一会发现T4好像用二维树状数组能做，但是复杂度不太划算，如果枚举左上右下两端点是O（n^5），就算去掉一维枚举长度也有O（n ^4），就能过20分。
当时还是贪了，想怎么优化一下过个50分赛后看来二维树状数组这个思路真是sb，老老实实DP就能拿70分……
结果时间到了1h还没想出来，及时止损先把20分拿了。
写完调完时间过了1.5h。
回过头来开出题人认为最简单的T1。
看了半个小时之后发现这就是一个模拟的大水题，什么线段树就是大炮打蚊子。
30min写完调完，切了切了。（此时过去2h）
然后看T2，仍然认为不可做，暴力都没什么思路，于是转去看T3。
看T3的时候我认为自己已经切了一道题，并且还写了一个暴力虽然分不多
所以还是信心满满的。
看到加上司的操作类似于树上倍增，但是由于其码量大，细节多，像我这种代码能力弱的一批的人肯定写不完，写完了也得调一辈子。
所以没敢往下想，就这样我和正解失之交臂……
否了树上倍增之后，发现加上司的操作类似于并查集合并，脑袋一热就想用并查集做。
加上司就合并，发文件就标记代表元，查询就查询该集合代表元是否标记。
有了这样的思路之后代码还是挺好写，50min想完写完调完。（此时过去2h50min）
最后还剩下1h10min做T2。
T2仍然没啥思路，本着不能固输的原则乱搞一通，过了样例花了50min。（当时我觉得自己220分在手，T2扔了就扔了吧……）
有上次inf开小挂分的经验，最后20min仔仔细细检查了inf，数组的大小，确保编译都能过防止lyn大佬行为 （这里埋下伏笔）。

交题之后我就高高兴兴去吃饭，觉得这把应该挺好，路上有想了想T3……
完蛋！出锅了！并查集好像没考虑元素和文件进入集合先后的问题，这样把它们扔到一起明显不合适！这题没了！
虽然这道题没了，但是想到我还有T1和T4的20分，还算说得过去，T3挂了就挂了把……

下午吃完饭会机房看成绩……WOC，0？？？？？？？？？？？？？？？！！！！！！！！！！！！
当时我人都傻了，T1就一个模拟怎么可能出锅？！T4怎么也没分？！
当时第一时间想到freopen可能错了。
打开T1的码，发现freopen没写错
那是怎么回事？！
打开数据点一看……
md，少一行判断重复提前的码！
当时真想扇自己几巴掌，怎么就没想到自己在造个特殊样例呢QAQ！
T1找出原因后去看T4的码，
赫然映入眼帘的是……

讯享网
我真tm无语了……
交卷前20分钟什么都检查了，就是忘了它！万万想不到在这出锅……
我之前还一直笑话别人freopen写错……
这下破案了：
脑抽：100->0
眼瞎：20->0
于是我成为了全机房唯一爆零的人……
当时真的afo的心都有了
这能说我不会吗？省选，NOI同步赛那种更难更正式的比赛都能掏个50多，这种小模拟为什么没有分？……运气原因？有但也不能说全是。
还是给大赛积累经验吧，模拟最好把小错都犯一遍，大赛就能避免了吧QAQ……

本次模拟赛积累经验*2：
1.无论多水的题都至少自己造三组特殊样例进行测试
2.检查freopen！！！

最后贴上正解和标程（我订正过来的就贴了我写的）：

T1提前

我们考虑从最终序列的首位开始填补数字：
逆序扫描操作序列，如果遇到一个之前没被扫描过的操作数，那么就把它填
入当前未填序列的首位。
扫描完成后，将剩余未填入的数按从小到大的顺序依次填入未填序列即可。

水题……

#include<bits/stdc++.h> using namespace std; int t,n,m,a[50005],b[50005],c[50005],d[50005],f[50005]; int main() { 
    // freopen("forward.in","r",stdin); // freopen("forward.out","w",stdout ); cin>>t; while(t--) { 
    memset(d,0,sizeof(d)); memset(f,0,sizeof(f)); cin>>n>>m; for(int i=1;i<=n;i++) a[i]=i; // for(int i=1;i<=m;i++) // { 
    // cnt=1; // cin>>pos; // b[1]=pos; // for(int i=1;i<=n;i++) if(a[i]!=pos) b[++cnt]=a[i];  for(int i=1;i<=cnt;i++) cout<<b[i]<<" ";  cout<<endl; // a[1]=pos; // for(int i=2;i<=cnt;i++) a[i]=b[i];  for(int i=1;i<=cnt;i++) cout<<a[i]<<" ";  cout<<endl; // }  cout<<pos; // for(int i=1;i<=cnt;i++) cout<<b[i]<<" "; for(int i=1;i<=m;i++) cin>>b[i],d[b[i]]++,f[b[i]]++; for(int i=m;i>=1;i--) { 
    if(d[b[i]]!=0) cout<<b[i]<<" ";//就少这一行啊！！！100分啊！！！ d[b[i]]=0; } for(int i=1;i<=n;i++) if(!f[a[i]]) cout<<a[i]<<" "; cout<<endl; } return 0; } /* 2 5 2 4 2 5 3 1 3 5 */ 

T2分篮子

将一个篮子的 ABC 三个价值看作三维空间中的点，那么我们就要用(x<=a)、
(y<=b)、(z<=c)这三个区域的并来覆盖所有的点，并且要使得 a+b+c 最小。
我们可以直接得到一个枚举算法——枚举 a,b,c，检查三个区域的并是否覆
盖了所有的点并更新答案，这样时间复杂度是 O(n³)的，可以得到 50 分。
而如果确定了 a，那接下来的任务就是将剩下未覆盖的点用(y<=b)和(z<=c)
覆盖，此时问题转化到了二维平面上（横坐标 b 纵坐标 c）
右图中，黑点表示某个未覆盖的篮子，而淡青
色的点则表示可能最优的 b,c 取值，可以看出，当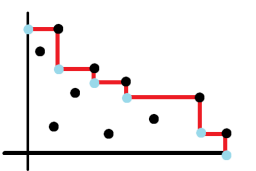

问题转化到二维平面上时，我们只要能求出黑点所
对应的红色阶梯形，再考虑红色阶梯形的每个淡青
色点处的解即可，而这显然是可以在 O(n)的时间
内求出来的，于是我们就有了一个 O(n²)的算法。
接下来，我们考虑对每一个枚举的 a 值维护这
样的 b,c 红色阶梯形并分别求出最优解——考虑
从大到小枚举 a 值，那么不能被(x<=a)覆盖的点便会越来越多，这些点需要被 bc
覆盖——在点逐渐被加入 bc 二维平面的过程中，阶梯形也会不停地发生变化。
注意到，维护阶梯形我们只需要维护在红色折线上的黑色点即可，而这可以
使用 C++STL 中的 set 来进行维护，也可以使用线段树（大致思路：先对权值离
散化，下标为离散化后的横坐标，维护的值为红色折线上该横坐标对应的纵坐标，
实现可能与这里描述的有差别）来维护红色折线以及淡青色点处的 b+c 最小值。
这样我们就得到了一个总时间复杂度 O(nlogn)的算法，足以通过本题。

思路是大概理解了，代码写不出来……可怜的代码能力

讯享网#include<bits/stdc++.h> using namespace std; inline int getint() { 
    char ch; while(!isdigit(ch=getchar())) ; int x=ch-'0'; while(isdigit(ch=getchar())) x=x*10+ch-'0'; return x; } const int N=; struct basket { 
    int a,b,c; }t[N]={ 
   }; bool basket_cmp(const basket &b1,const basket &b2) { 
    return b1.a>b2.a; } int n; typedef pair<int,int> point; typedef set<point> point_list; void init() { 
    n=getint(); for(int i=1;i<=n;++i) t[i].a=getint(),t[i].b=getint(),t[i].c=getint(); t[n+1]=(basket){ 
   0,0,0}; sort(t+1,t+n+1,basket_cmp); } void work() { 
    long long ans=t[1].a; point_list m; m.insert(make_pair(,0)); m.insert(make_pair(0,)); multiset<int> v; v.insert(0); for(int i=1;i<=n;++i) { 
    point p(t[i].b,t[i].c); if(m.count(p)) continue; m.insert(p); point_list::iterator next=m.find(p); point_list::iterator last=next++,it=last--; if(it->second <= next->second) m.erase(it); else { 
    v.insert(it->first + next->second); v.insert(last->first + it->second); v.erase(v.find(last->first + next->second)); while(it->second >= last->second) { 
    --last,--it,--next; v.erase(v.find(last->first + it->second)); v.erase(v.find(it->first + next->second)); v.insert(last->first + next->second); m.erase(it); it=m.find(p); last=it,--last; next=it,++next; } } ans=min(ans,((long long)t[i+1].a)+*v.begin()); } cout<<ans<<endl; } int main() { 
    freopen("basket.in","r",stdin); freopen("basket.out","w",stdout); int T=getint(); while(T--) { 
    init(); work(); } return 0; } 

T3管理

显然，该问题就相当于进行一系列的任命上司操作，并且记录一系列的时间
戳，并且询问在某个时间戳的时候某个人是否是另一个人的上司（直接或间接）。
首先，我们可以先读入所有的操作，在每次 2 操作记录时间戳的时候就回答
与这个时间戳相关联的所有问题（即 3 操作询问某人是否读过这次 2 操作的文
件，转换一下就是某人是否是这次 2 操作收到文件的人的上司）
对于测试点 1-4，使用简单粗暴的算法即可通过。
对于测试点 5-10，我们注意到，若询问 i 是否是 j>i 的上司，只需要判断
是否分别有 i 是 i+1 上司的任命，i+1 是 i+2 上司的任命……一直到是否有 j-1 是 j 的上司的任命即可，而这个可以使用并查集实现——若任命 i 是 i+1 的上
司，就将 i 和 i+1 的连通块连接起来，询问 i 是否是 j>i 的上司也等价于询问 i 和 j 是否连通——当 i 到 j 之间的全部任命都完成时，i 和 j 之间也就是连通的
了。
而对于测试点 11-16，在记录时间戳和询问的时候不会再有新的任命信息进
行干扰，那么 1 操作相当于构造了一个上司森林，判断上司的问题也就转化为询
问一个点 A 是否是某个点 B 的祖先，而这个判断可以使用树上倍增、树的 DFS 序
等多种方式解决，这里就不一一赘述了。
而将以上两个方面结合起来，并考虑到一个人的直接上司一旦被任命之后便
不会更改，我们就得到了标准解法：
在某个时间戳时 A 是 B 的上司，等价于以下两个条件同时成立：
1、所有 1 操作完成后 A 是 B 的上司（与测试点 11-16 的处理类似，只不过
实现时是先扫一遍，无视 2、3 操作而处理所有 1 操作，之后再扫一遍，无视 1
操作而处理 2、3 操作）
2、在该时间戳时 A 和 B 是连通的（连通的相关处理与测试点 5-10 类似）。

我否掉的思路居然是正解，就离谱……要是能写出来这题就切了……

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+5; int n,m; struct edge { 
    int to,nxt,w; }e[maxn]; struct file { 
    int x,t; }fi[maxn]; struct ask { 
    int x,id; }as[maxn]; int head[maxn],ecnt,cnt1,cnt2,cnt; void add(int x,int y,int z) { 
    e[++ecnt]=(edge){ 
   y,head[x],z}; head[x]=ecnt; } int dfn[maxn],siz[maxn],f[maxn][21],ti[maxn][21],dep[maxn],ru[maxn],mi[21]; void dfs(int u,int fa) { 
    dfn[u]=++cnt;siz[u]=1; for(int i=head[u];i;i=e[i].nxt) { 
    int v=e[i].to; if(v==fa) continue; f[v][0]=u;ti[v][0]=e[i].w; dep[v]=dep[u]+1; dfs(v,u); siz[u]+=siz[v]; } return; } void init() { 
    mi[0]=1; for(int i=1;i<=18;i++) mi[i]=mi[i-1]<<1; for(int i=1;i<=18;i++) { 
    for(int j=1;j<=n;j++) { 
    if(dep[j]<mi[i]) continue; int tr=f[j][i-1]; f[j][i]=f[tr][i-1]; ti[j][i]=max(ti[j][i-1],ti[tr][i-1]); } } return; } bool judge(int x,int y) { 
   return dfn[y]>=dfn[x]&&dfn[y]<=dfn[x]+siz[x]-1;} bool solve(ask fa) { 
    int u=fi[fa.id].x,v=fa.x; if(!judge(v,u)) return false; for(int i=18;i>=0;i--) { 
    if(dep[u]<mi[i]) continue; if(ti[u][i]>fi[fa.id].t) continue; u=f[u][i]; } return dep[u]<=dep[v]; } int main() { 
    cin>>n>>m; int op,a,b; for(int i=1;i<=m;i++) { 
    cin>>op; if(op==1) cin>>a>>b,add(b,a,i),ru[a]++; if(op==2) cin>>b,fi[++cnt1].t=i,fi[cnt1].x=b; if(op==3) cin>>a>>b,as[++cnt2].id=b,as[cnt2].x=a; } for(int i=1;i<=n;i++) if(!ru[i]) dfs(i,0); init(); for(int i=1;i<=cnt2;i++) { 
    if(solve(as[i])) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; } /* 4 9 1 4 3 2 4 3 3 1 1 2 3 2 2 3 1 2 1 3 1 2 2 3 1 3 */ 

T4正方形

题目来源：https://codeforces.com/contest/480/problem/E
考虑使用时间倒流方法来进行处理——将正向的空地变成障碍物的操作倒
流成反向的，将障碍物变为空地的操作。
假设矩阵在修改前有一个最大全空地正方形边长 ans，消除一个障碍物后，
所有可能的新产生的最优正方形必然经过这次修改的位置。
这样我们每次只需要在修改位置所在行重新计算一遍穿过该行的最大全空
地正方形的边长：在该行枚举正方形可能的右端点 r ，高效找对应最优左端点的
工作需要使用单调队列来完成。
预处理出每个位置往上连续走和往下连续走能走多长距离（每次修改操作后
需要更新修改位置所在列的数据），枚举正方形时从左往右扫，使用单调队列维
护当前右端点 r 为正方形右侧边界的时候，正方形可能的上边界范围与下边界范 围随选取左端点变化的取值：
对于一个左端点的位置 l ， l 能成为正方形的左边界，当且仅当单调队列中
位置 l 处往上和往下合起来提供了至少 r − l 的高度，同时注意到，随着 r 右移，
最靠左的合法的 l 也会随之右移，在往右扫维护单调队列的同时也可以算出结果。
如果想使用在线做法，可以考虑使用分治方式+线段树解决，不过这个做法
编写&运行耗时都相对长一些。

正解思路懂了，码没写完……不过改完之后70分的暴力是真的香

讯享网#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int N=2020,M=2020,K=2020; int n,m,k,up[N][M]={ 
   },down[N][M]={ 
   }; int q1[M]={ 
   },q2[M]={ 
   },v1[M]={ 
   },v2[M]={ 
   },x[K]={ 
   },y[K]={ 
   }; char ch[N][M]={ 
   }; void update(int p) { 
    for(int i=1;i<=n;++i) up[i][p]=ch[i][p]=='X' ? 0 : up[i-1][p]+1; for(int i=n;i>=1;--i) down[i][p]=ch[i][p]=='X' ? 0 : down[i+1][p]+1; } void init() { 
    scanf("%d%d%d\n",&n,&m,&k); for(int i=1;i<=n;++i) scanf("%s\n",ch[i]+1); } int calc(int mid) { 
    int h1=1,t1=0,h2=1,t2=0,pos=1,ans=0; for(int j=1;j<=m;++j) { 
    while(pos==j || pos-j <= v1[h1]+v2[h2]-1) { 
    ans=max(ans,pos-j); if(pos<=m) { 
    while(h1<=t1 && up[mid][pos]<=v1[t1]) --t1; ++t1,q1[t1]=pos,v1[t1]=up[mid][pos]; while(h2<=t2 && down[mid][pos]<=v2[t2]) --t2; ++t2,q2[t2]=pos,v2[t2]=down[mid][pos]; ++pos; } else break; } if(q1[h1]==j) ++h1; if(q2[h2]==j) ++h2; } return ans; } void work() { 
    for(int i=1;i<=k;++i) { 
    scanf("%d%d",&x[i],&y[i]); ch[x[i]][y[i]]='X'; } for(int j=1;j<=m;++j) update(j); int ans[K]={ 
   }; for(int i=1;i<n;++i) ans[k]=max(ans[k],calc(i)); for(int i=k;i>=1;--i) { 
    ch[x[i]][y[i]]='.'; update(y[i]); ans[i-1]=max(ans[i],calc(x[i])); } for(int i=1;i<=k;++i) printf("%d\n",ans[i]); } int main() { 
    freopen("square.in","r",stdin); freopen("square.out","w",stdout); init(); work(); fclose(stdin); fclose(stdout); return 0; }