2025年数学建模（6）图论

科技前沿 • 2025-03-19 14:21 • 阅读 91

大家好，我是讯享网，很高兴认识大家。

图定点与边组成的集合
G=(V(G),E(G))
V(G)定点集合
E(G)边的集合

有向图
边均为有序偶对，即每一条边都有确定的方向和指向，有头有尾

无向图
边均为无序偶对，即每一条边都没有方向和指向

混合图
既有有向边也有无向边的图

关联
边和它两端定点相互关联

相邻
与同一边关联的两个定点称为相邻，与同一点关联的边相邻

环，连杆
端点重合的一边称为环，端点不同的称为连杆

重边
一对定点之间有多条边

简单图
没有环和重边的图

赋权图
图中的每一条边被赋上相应的权重，则图与边上的权统称为赋权图

图的定点度
对于定点与其相关联的边数为其度数，对于有向图，从该点引出的边数为出度，引入的边数为入度

奇点和偶点度数为奇数的顶点为奇点，为偶数的顶点为偶点
一条边对应两个度

树
连通且不含圈的无向图成为树，以T表示
树中的边称为树枝，度为1的定点被称为树叶

邻接矩阵（很重要）
通过图中的点为cols和rows，对于图中对应的（col，row）的值即为两相邻定点所所关联的边的权重，而对于有向图有向为1，反向为0，对于不相邻的定点所对应矩阵元素的值为零，矩阵对角线为0
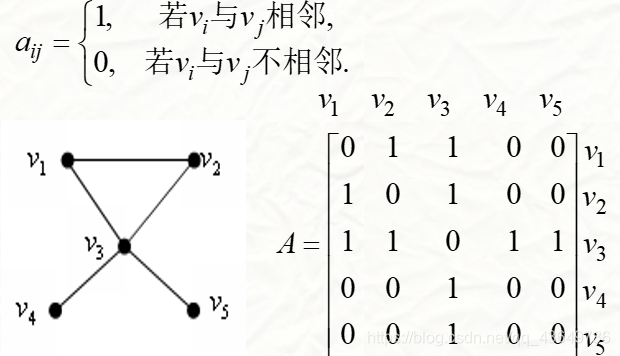
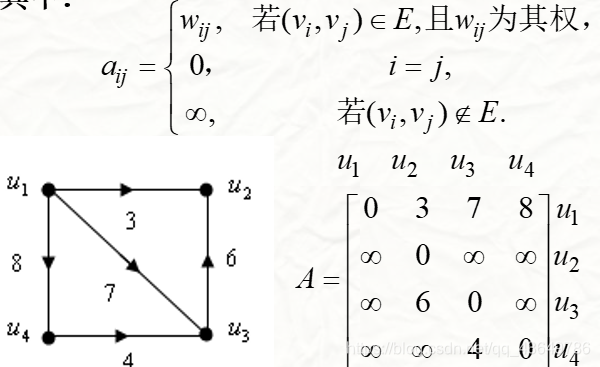
在这里插入图片描述

有向赋权图
在相邻的定点的边赋有权重的图，一般解决实际问题大多为有向赋权图，其中的权重大部分表示所需的时间，付出的代价等等
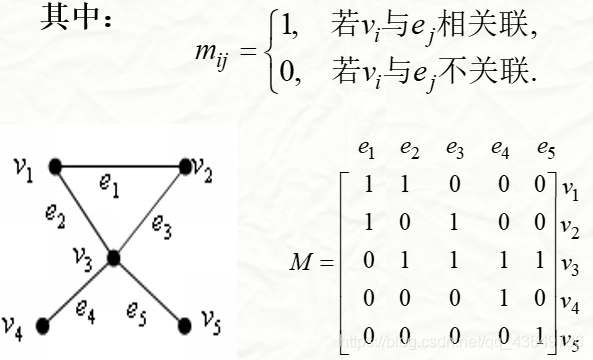
在这里插入图片描述
关联矩阵
图中对应的矩阵定点间所对应的矩阵元素，关联则为1，不关联则为0

有向图关联矩阵
正向的路为1，反向的路为-1

目的：
1.求赋权图中从给定点到其余顶点的最短路
2.求赋权图中任意两点间的最短路

最小生成树算法及其matlab的实现与结果解读