
讯享网
 作者简介:尹锋,一级教师,从教11年,参与6轮高三备考,培养近千余人学生考上本科大学,2018年培养了从教生涯来首个清华大学生。主持区级课题一项,参与区级课题一项,发表教育教学论文2篇。曾获“汉滨区教学能手”,“汉滨区优秀教师”,“高新区优秀教师”,“高新区教育先进个人”, “高新区优秀班主任”,“优秀备课组长”等荣誉称号
作者简介:尹锋,一级教师,从教11年,参与6轮高三备考,培养近千余人学生考上本科大学,2018年培养了从教生涯来首个清华大学生。主持区级课题一项,参与区级课题一项,发表教育教学论文2篇。曾获“汉滨区教学能手”,“汉滨区优秀教师”,“高新区优秀教师”,“高新区教育先进个人”, “高新区优秀班主任”,“优秀备课组长”等荣誉称号
[摘要]:因式分解贯穿整个数学学科,一元二次多项式的因式分解的应用更是无处不在。本文将给出高等数学中因式分解思想在初等数学中的一个应用。给出整系数一元二次多项式因式分解判定定理:整系数多项式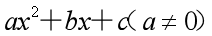 可分解为两个整系数一次多项式之积的充要条件是:
可分解为两个整系数一次多项式之积的充要条件是: 为完全平方数。并将定理推广至有理系数范围。
为完全平方数。并将定理推广至有理系数范围。
[关键词]:有理系数、整系数、一元二次多项式、因式分解、因式分解的判定。
首先引入几个概念:
多项式:n是一个非负整数,形式表达式 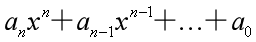 ,其中
,其中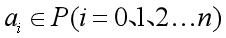 称为数域
称为数域 上的一元多项式。
上的一元多项式。
八年级我们初识因式分解,从此因式分解就和我们的数学学习分不开了,尤其是在整个中学阶段要学习的代数式化简、一元二次方程的根,一元二次函数等模块的应用。
我们知道有些多项式容易分解,有些多项式难分解,还有些多项式不能分解,并且很多时候因式分解的应用都在有理系数上讨论。既然要分解因式,首先得判断所给的多项式能不能因式分解,如果不能,显然就不用分解了,也就没必要费大力气去寻找分解方法了。那问题出来了,在初等数学中如何判定一个多项式能否因式分解呢?
纵观初等数学中有关因式分解的方法:
1、基本公式法(包括十字相乘法)

2、待定系数法
3、利用多项式对应方程的根来分解因式
基本公式法(包括十字相乘法)具有很大局限性,仅能判定少数具有基本公式型的多项式的因式分解情况;虽然待定系数法几乎能够判定所有的多项式能否因式分解,但运算能力的要求是相当高的,学生能力达不到,老师也不提倡;利用多项式的根分解,是一个较实用的方法,那得先求根,如果求根再需要用到因式分解,那又该怎么办呢?
寻求一个初等的能够快速的判定一个多项式能否因式分解的方法,还是很有意义的。本文将带领读者共同来寻找有理数域上一个有理系数一元二次多项式的因式分解的判定方法,思路分两步分析:
一、从高等数学的角度分析:
高等数学中有关因式分解的定理:
有理根判定定理[1]:

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/27819.html