几张卡牌 排成一行，每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。 每次行动，你可以从行的开头或者末尾拿一张卡牌，最终你必须正好拿 k 张卡牌。 你的点数就是你拿到手中的所有卡牌的点数之和。 给你一个整数数组 cardPoints 和整数 k，请你返回可以获得的最大点数。

示例 1：

输入：
cardPoints = [1,2,3,4,5,6,1], k = 3
输出：
12
解释：第一次行动，不管拿哪张牌，你的点数总是 1 。
但是，先拿最右边的卡牌将会最大化你的可获得点数。
最优策略是拿右边的三张牌，最终点数为 1 + 6 + 5 = 12 。

示例 2：

输入：
cardPoints = [2,2,2], k = 2
输出：4
解释：无论你拿起哪两张卡牌，可获得的点数总是 4 。

示例 3：

输入：
cardPoints = [9,7,7,9,7,7,9], k = 7
输出：55
解释：你必须拿起所有卡牌，可以获得的点数为所有卡牌的点数之和。

示例 4：

输入：
cardPoints = [1,1000,1], k = 1
输出：1
解释：你无法拿到中间那张卡牌，所以可以获得的最大点数为 1 。

示例 5：

讯享网

输入：
cardPoints = [1,79,80,1,1,1,200,1], k = 3
输出：202

提示：

1 <= cardPoints.length <= 10^5
1 <= cardPoints[i] <= 10^4
1 <= k <=cardPoints.length

（1）超时的DFS

最开始想到的是 dfs，从最开始的节点出发，要么选左，要么选右， 选择了一边之后如果还能选，那再继续上述过程，这不就是一棵树，然后就按dfs写的，但在用例较长的情况下超时了，只通过了 15/40 的样例。 提供一种思考的思路，耗时过多，没法通过本题。
python

class Solution: def maxScore(self, cardPoints: List[int], k: int) -> int: if k == len(cardPoints): return sum(cardPoints) scores = 0 def dfs(points, k, l, r, scores): if k == 1: # 边界条件，只能选一次的话，就选左或者右中的较大者 return max(points[l], points[r]) l_max = dfs(points, k - 1, l + 1, r, scores) + points[l] # 选择左边的情况，并继续向下dfs r_max = dfs(points, k - 1, l, r - 1, scores) + points[r] # 选择右边的情况，并继续向下dfs return max(l_max, r_max) # 返回选左或者选右的较大者 return dfs(cardPoints, k, 0, len(cardPoints) - 1, scores) 

（2）前缀和求解

前缀和写法，先求个前缀和，再求left(0-k) + right(k-i) 区间最大解即可
java

讯享网 public int maxScore2(int[] cardPoints, int k) { 
    int len = cardPoints.length; int[] pre = new int[len + 1]; pre[0] = 0; for (int i = 0; i < len; i++) { 
    pre[i + 1] = cardPoints[i] + pre[i]; } int max = -1; for (int i = 0; i <= k; i++) { 
    max = Math.max(max, pre[i] + pre[len] - pre[len - k + i]); } return max; } 

（3）暴力求解（贪心思想）

先求出前k个数的总和，然后前面去掉一个，后面加上一个，前面去掉一个，后面加上一个，求最大值就好了
java

 public int maxScore(int[] cardPoints, int k) { 
    int s = 0; int t = k; for (int i = 0; i < k; i++) { 
    s += cardPoints[i]; } int max = s; for (int i = cardPoints.length - 1; i >= cardPoints.length - k; i--) { 
    s = s - cardPoints[--t] + cardPoints[i]; max = Math.max(s, max); } return max; } 

（4）滑窗思想

逆向思维，按题中意思取左取右得最大值，反过来就是求中间连续子数组得和最小, 由于要取 k 张牌，所以反过来就是在中间找连续的长度为len(carPoints)-k 的子数组使其和最小，滑窗将移动 k 次，不断更新滑窗能得到和的最小值， 最后用输入数组的和减去这个最小值就是结果。主要还是算清楚滑窗的左右边界和题中已知量的关系。
下面举一个范例

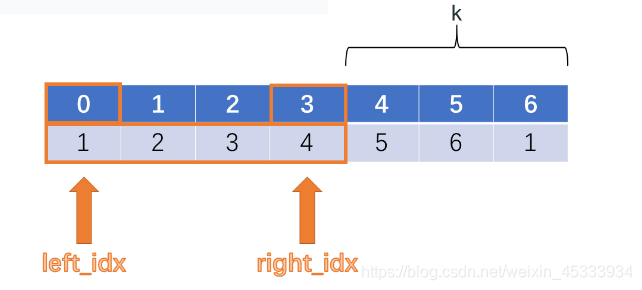
第一次移动

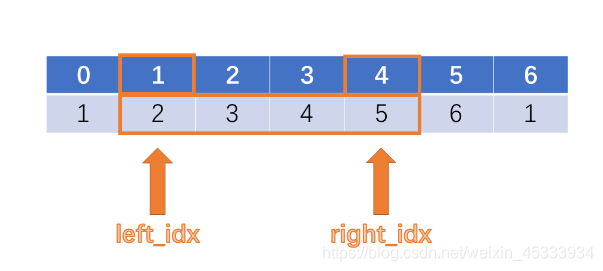
第二次移动

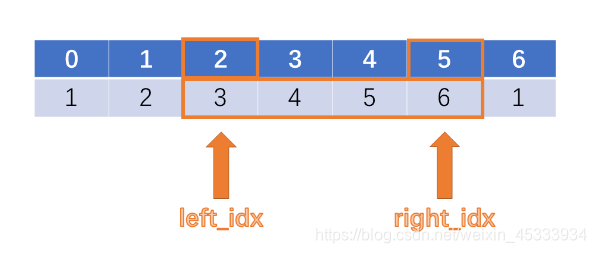
第三次移动

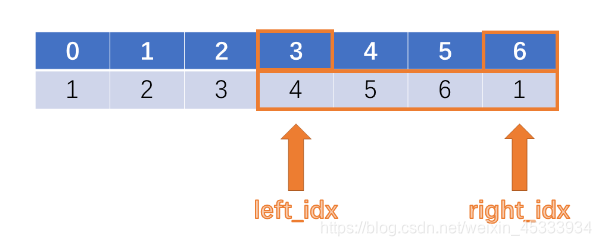
python

讯享网 class Solution: def maxScore(self, cardPoints: List[int], k: int) -> int: if len(cardPoints) == k: # 如果取的次数等于长度，说明把所有牌都取走，直接返回总和 return sum(cardPoints) # 逆向思维，按题中意思取左取右得最大值，反过来就是求中间连续子数组得和最小 # 由于要取 k 张牌，所以反过来就是在中间找连续的长度为 len(carPoints)-k 的子数组使其和最小，这以部分就是滑动窗口 res_opposite = sum(cardPoints[:len(cardPoints) - k]) # 变量存储滑窗的最小值，这里先按初始位置赋初值 current_sum = res_opposite # current_sum记录当前滑窗总和 left_idx, right_idx = 0, len(cardPoints) - k - 1 # 设定滑窗边界 for _ in range(k): # 滑窗将移动 k 次 left_idx += 1 # 更新滑窗左右边界 right_idx += 1 # 计算新位置滑窗内值的总和，减去滑窗原来的左边界，加上滑窗新的右边界 current_sum = current_sum - cardPoints[left_idx - 1] + cardPoints[right_idx] res_opposite = min(res_opposite, current_sum) # 更新最小的滑窗范围内的和 return sum(cardPoints) - res_opposite 

（5）滑窗的另一种解法

java

 public int maxScore3(int[] cardPoints, int k) { 
    int sumk = 0; int max = Integer.MIN_VALUE; // 求出数组前k个 的 总和 for (int i = 0; i < k; i++) { 
    sumk += cardPoints[i]; } max = Math.max(max, sumk); int left = cardPoints.length - 1; for (int i = k - 1; i >= 0; i--) { 
    sumk = sumk - cardPoints[i] + cardPoints[left]; left--; max = Math.max(max, sumk); } return max; } 

不经历风雨,怎能在计算机的大山之顶看见彩虹呢！ 无论怎样，相信明天一定会更好！！！！！