| 触碰标题下面一行的“邵勇老师”查看所有文章;触碰“数学教学研究”, 关注本微信公众号(sx100sy)。本公众号内容均由邵勇(北京)本人独创,欢迎转发,但未经许可不能转载。每周推送两到三篇内容上有份量的数学文章,但在行文上力争做到深入浅出。几分钟便可读完,轻松学数学。 |
上一讲讲了琴生不等式,这次本来想讲一讲幂平均不等式,但觉得杨格不等式比较简单,也有朋友在留言中提到,所以,本期就先介绍杨格不等式。而幂平均不等式就留到下一讲吧。
琴生不等式 函数f(x)是定义在开区间(a,b)上的凸函数。设λ1, λ2, ··· , λn是n个正实数,λ1+λ2+···+λn=1。x1, x2, ··· , xn 是开区间(a,b)上任意n个点,则下面不等式成立: 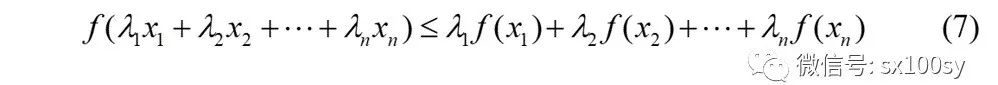 讯享网这个不等式称为琴生不等式。(注意,这里所说的凸函数是下凸函数。)若取λ1=λ2=···=λn=1/n,则上面的(7)式将成为: 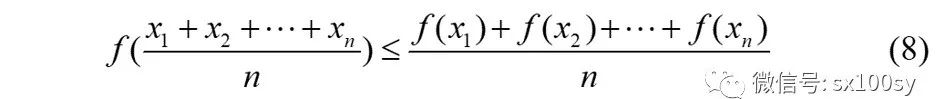 (8)式也是琴生不等式,它是(7)式的特殊情况。有时人们把(8)这种简单一些的形式称为琴生不等式,把(7)这种一般些的形式称为加权琴生不等式。(很多人也给出过(8)式的证明方法,我上一期则是给出(7)式的证明。这些都是可以的。)若上面琴生不等式(7)和(8)的定义中,f(x)是凹函数(上凸函数),则(7)式和(8)式中的小于等于号“≤”就变为大于等于号“≥”,分别成为下面的(7')式和(8')式: (8)式也是琴生不等式,它是(7)式的特殊情况。有时人们把(8)这种简单一些的形式称为琴生不等式,把(7)这种一般些的形式称为加权琴生不等式。(很多人也给出过(8)式的证明方法,我上一期则是给出(7)式的证明。这些都是可以的。)若上面琴生不等式(7)和(8)的定义中,f(x)是凹函数(上凸函数),则(7)式和(8)式中的小于等于号“≤”就变为大于等于号“≥”,分别成为下面的(7')式和(8')式: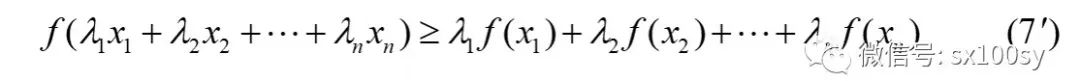 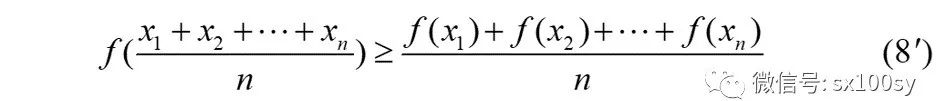 |
从琴生不等式出发推导其他不等式,需要选取恰当的函数f(x)。比如选择 f (x ) = ln x。因为这个对数函数是上凸函数,所以由(8')式,得
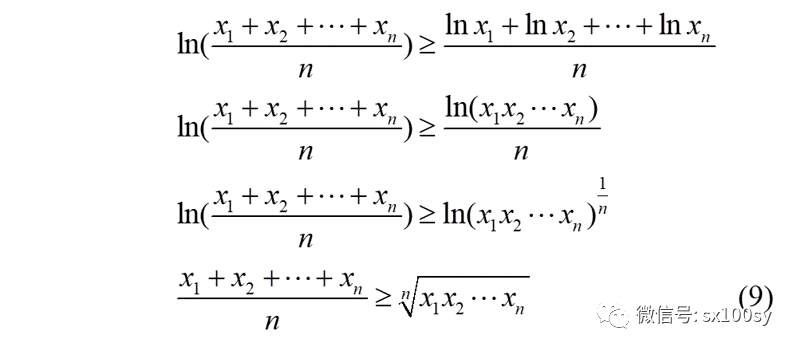
即n个正数的算术平均值大于等于它们的几何平均值。这就是所谓的平均不等式,或叫做均值不等式,或明确一些,叫做算术-几何平均不等式。这个不等式是最为常用的不等式,前几期也从不同角度说到这个不等式。在n=2时,就得到更加常用的均值不等式:
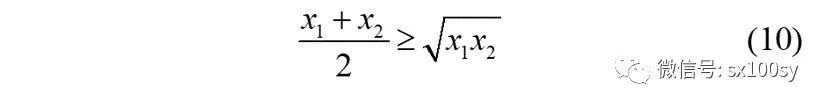
您可能会觉得这个均值不等式过于简单了,那好的,我下面讲一讲它的推广——杨格不等式(Young Inequality)。因为存在两种形式的琴生不等式(一个是一般的,一个是特殊的),所以既然存在均值不等式,那么就一定存在与均值不等式对应的另一个不等式,这就是杨格不等式。想要探出个究竟,请跟我来!
同样考虑对数函数 f (x ) = ln x。我们应用一般形式的琴生不等式(7'),取n=2,演化过程如下:
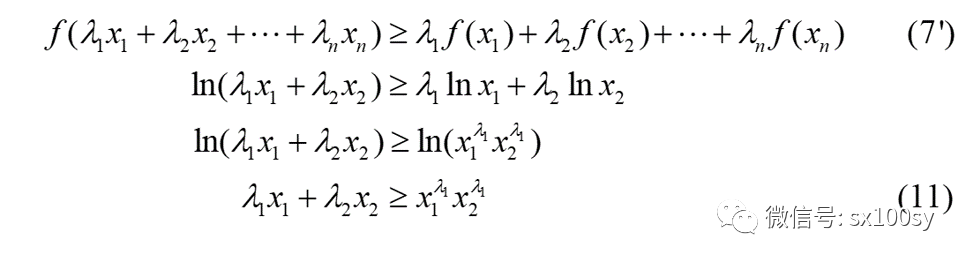
我们把(11)式与(10)式进行比较:
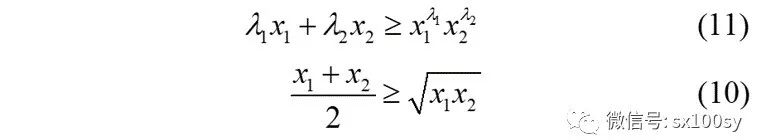

发现,在λ1=λ2=1/2时,(11)式就成为(10)式。
但我们知道,琴生不等式中的λi ( i=1,2,3,···,n ) 介于0与1之间,所以,对n=2的情况,我们把λ1和λ2分别写成分数的形式:
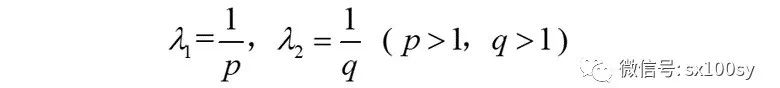
当然,依然有:
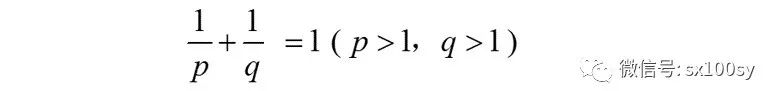
又因为n=2,所以,把x1和x2换成a和b。于是,由(11)式,便得到著名的杨格不等式:
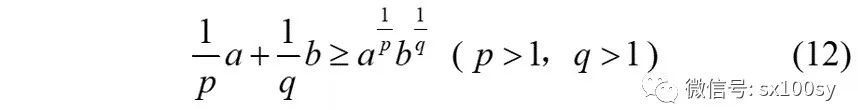
以上我们就从琴生不等式推导出了杨格不等式。
其实,上面的(12)式只是杨格不等式的一部分,还有不等号反向的情况,我们从琴生不等式得不出来。但我开始时说过,另有一种办法可以得到杨格不等式,这种办法可以得到含(12)式在内的两种情况。这里我就不具体写出这第二种方法了,只给出下面两个不等式(x>0时成立),利用它们即可做到。
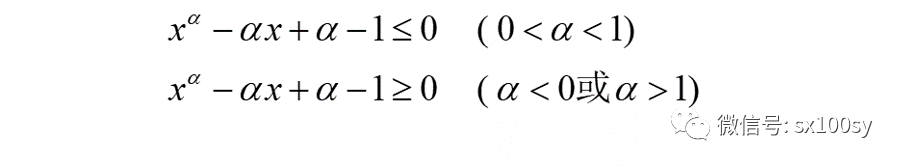


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/24273.html